人教版七年级下册9.3一元一次不等式组 课件(共23张PPT)
文档属性
| 名称 | 人教版七年级下册9.3一元一次不等式组 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第九章 不等式与不等式组
一元一次不等式组
学习目标
1.了解一元一次不等式组的概念.
2.理解一元一次不等式组的解集的意义,掌握求一元一次不等式组的解集的方法.
3.(课标)会用数轴确定由两个一元一次不等式组成的不等式组的解集.
知识点一:一元一次不等式组
(1)类似于方程组,把几个具有相同未知数的一元一次
合起来,就组成一个一元一次不等式组.
(2)判断一个不等式组是否为一元一次不等式组,要考虑以下两个方面:①组成不等式组的每个不等式必须是一元一次不等式;②整个不等式组中只含 个未知数.
一
知识要点
不等式
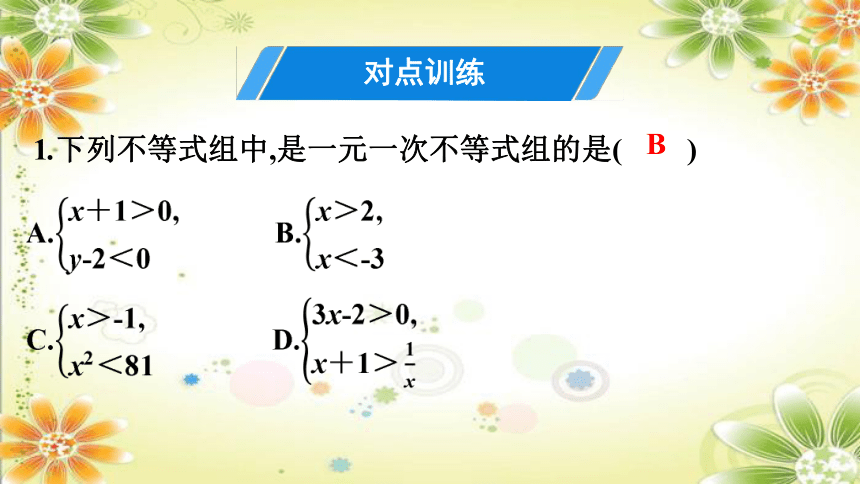
1.下列不等式组中,是一元一次不等式组的是( )
对点训练
B
知识点二:一元一次不等式组的解集
(1)类似于方程组的解,一般地,几个不等式的解集的
部分,叫做由它们所组成的不等式组的 .
解集
公共
(2)由两个一元一次不等式组成的不等式组的解集的四种基本类型如下表所示:
2.用数轴表示下列各组不等式组的解集,并写出解集:
数轴表示略
-1<x<1 x>2
(3) (4)
x<-8 无解
知识点三:解一元一次不等式组
(1)解不等式组就是求它的 .
(2)解一元一次不等式组的步骤:
①分别求出不等式组中各个不等式的解集;
②将各个不等式的解集在数轴上表示出来;
③在数轴上找出各个不等式的解集的公共部分,这个公共部分就是不等式组的解集.
(3)画数轴表示解集时,要牢记:大于向右画,小于向左画,有等号画实心圆点,无等号画空心圆圈.
解集
(4)原不等式组的解集为 .
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在如图所示的数轴上表示出来:
-1<x≤2
x≤2
x>-1
数轴略
4.【例1】下列不是一元一次不等式组的是( )
精典范例
C
5.【例2】写出下列各不等式组的解集:
x>2
3无解
x<-4
(4)
(2)
x≥1
.根据下列数轴写出各不等式组的解集:
(1)
(3)
-2≤x≤1
无解
x≤-2
x≥3,数轴略
-1≤x<3,数轴略
9(人教7下P130)把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本 共有多少人
10某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人.问该校初三年级共有多少人参加春游
解:由3x+1≥2(x-1),得x≥-3.
由2(x+1)>4x,得x<1.
∴不等式组的解集为-3≤x<1.
解集在数轴上表示如图所示:
∴不等式组的解集是x>3.
解不等式①,得x>3,解不等式②,得x≥1.
解集在数轴上表示如图所示:
(1)当a=3时,解这个不等式组;
(2)若不等式组的解集是x<1,求a的值.
解:(1)当a=3时,
由①得2x+8>3x+6,解得x<2,
由②得x<3,∴原不等式组的解集是x<2.
(2)由①得x<2,由②得x<a,
而不等式组的解集是x<1,∴a=1.
感谢大家!
第九章 不等式与不等式组
一元一次不等式组
学习目标
1.了解一元一次不等式组的概念.
2.理解一元一次不等式组的解集的意义,掌握求一元一次不等式组的解集的方法.
3.(课标)会用数轴确定由两个一元一次不等式组成的不等式组的解集.
知识点一:一元一次不等式组
(1)类似于方程组,把几个具有相同未知数的一元一次
合起来,就组成一个一元一次不等式组.
(2)判断一个不等式组是否为一元一次不等式组,要考虑以下两个方面:①组成不等式组的每个不等式必须是一元一次不等式;②整个不等式组中只含 个未知数.
一
知识要点
不等式
1.下列不等式组中,是一元一次不等式组的是( )
对点训练
B
知识点二:一元一次不等式组的解集
(1)类似于方程组的解,一般地,几个不等式的解集的
部分,叫做由它们所组成的不等式组的 .
解集
公共
(2)由两个一元一次不等式组成的不等式组的解集的四种基本类型如下表所示:
2.用数轴表示下列各组不等式组的解集,并写出解集:
数轴表示略
-1<x<1 x>2
(3) (4)
x<-8 无解
知识点三:解一元一次不等式组
(1)解不等式组就是求它的 .
(2)解一元一次不等式组的步骤:
①分别求出不等式组中各个不等式的解集;
②将各个不等式的解集在数轴上表示出来;
③在数轴上找出各个不等式的解集的公共部分,这个公共部分就是不等式组的解集.
(3)画数轴表示解集时,要牢记:大于向右画,小于向左画,有等号画实心圆点,无等号画空心圆圈.
解集
(4)原不等式组的解集为 .
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在如图所示的数轴上表示出来:
-1<x≤2
x≤2
x>-1
数轴略
4.【例1】下列不是一元一次不等式组的是( )
精典范例
C
5.【例2】写出下列各不等式组的解集:
x>2
3
x<-4
(4)
(2)
x≥1
.根据下列数轴写出各不等式组的解集:
(1)
(3)
-2≤x≤1
无解
x≤-2
x≥3,数轴略
-1≤x<3,数轴略
9(人教7下P130)把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本.这些书有多少本 共有多少人
10某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人.问该校初三年级共有多少人参加春游
解:由3x+1≥2(x-1),得x≥-3.
由2(x+1)>4x,得x<1.
∴不等式组的解集为-3≤x<1.
解集在数轴上表示如图所示:
∴不等式组的解集是x>3.
解不等式①,得x>3,解不等式②,得x≥1.
解集在数轴上表示如图所示:
(1)当a=3时,解这个不等式组;
(2)若不等式组的解集是x<1,求a的值.
解:(1)当a=3时,
由①得2x+8>3x+6,解得x<2,
由②得x<3,∴原不等式组的解集是x<2.
(2)由①得x<2,由②得x<a,
而不等式组的解集是x<1,∴a=1.
感谢大家!
