湖北省随州市广水市2022-2023学年九年级下学期3月统一考试数学试卷(含答案)
文档属性
| 名称 | 湖北省随州市广水市2022-2023学年九年级下学期3月统一考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 735.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 16:09:17 | ||
图片预览




文档简介
广水市2023年九年级三月统一考试
数学试题
(测试时间120分钟 满分120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卷上,并将准考证号条形码粘贴在答题卷上的指定位置。
2.选择题每小题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答在试题卷上无效。
3.非选择题的作答:用0.5毫米黑色墨水签字笔直接答在答题卷上对应的答题区域内。答在试题卷上无效。
4.考生必须保持答题卷的整洁。考试结束后,请将本试题卷和答题卷一并上交。
一、选择题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的)
1.2023的相反数是
A. B. C.2023 D.-2023
2.我国的天问一号火星探测器成功着陆火星,据测算,地球到火星的最近距离约为55000000千米,数据55000000用科学记数法表示为
A. B. C. D.
3.如图,将三角尺的直角顶点放在直尺的一边上,,,则∠3的度数等于
A.20° B.25° C.30° D.35°
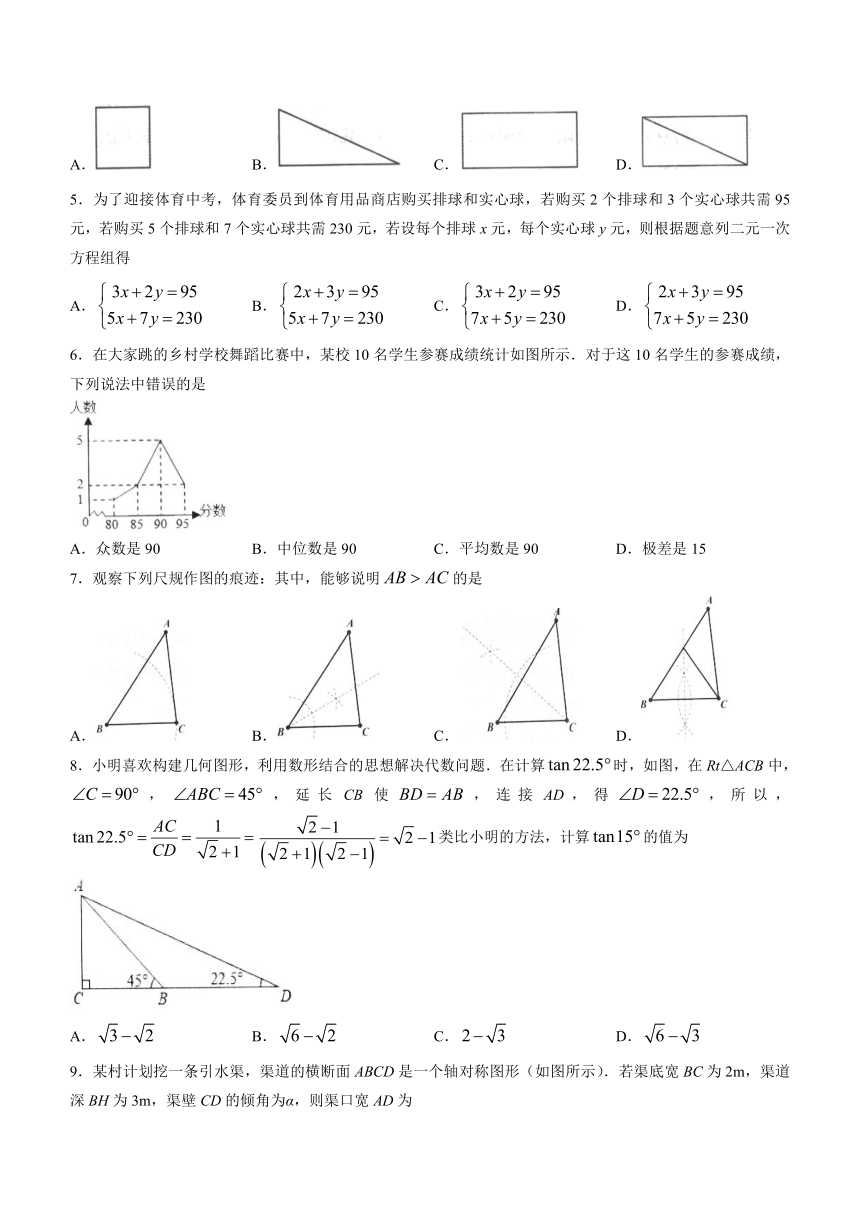
4.如图①用一个平面截长方体,得到如图②的几何体,它在我国古代数学名著《九章算术》中被称为堑堵.图②堑堵的俯视图是
A. B. C. D.
5.为了迎接体育中考,体育委员到体育用品商店购买排球和实心球,若购买2个排球和3个实心球共需95元,若购买5个排球和7个实心球共需230元,若设每个排球x元,每个实心球y元,则根据题意列二元一次方程组得
A. B. C. D.
6.在大家跳的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是
A.众数是90 B.中位数是90 C.平均数是90 D.极差是15
7.观察下列尺规作图的痕迹:其中,能够说明的是
A. B. C. D.
8.小明喜欢构建几何图形,利用数形结合的思想解决代数问题.在计算时,如图,在Rt△ACB中,,,延长CB使,连接AD,得,所以,类比小明的方法,计算的值为
A. B. C. D.
9.某村计划挖一条引水渠,渠道的横断面ABCD是一个轴对称图形(如图所示).若渠底宽BC为2m,渠道深BH为3m,渠壁CD的倾角为α,则渠口宽AD为
A. B. C. D.
10.如图,抛物线的对称轴是直线,并与x轴交于A,B两点,若,则下列结论中:①;②;③;④若m为任意实数,则,正确的个数是
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题)
二、填空题(共18分,只需要将结果直接填写在答题卡对应题号处的横线上)
11.计算: .
12.设,是一元二次方程的两根,则 .
13.圆材埋壁是我国古代数学名著《九章算术》中的一个问题:今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?.用现在的几何语言表达即:如图,CD为⊙O的直径,弦,垂足为点E,寸,寸,则直径CD的长度是 寸.
14.如图是用七巧板拼成的正方形桌面,一个小球在桌面上自由地滚动,它最终停在黑色区域的概率是 .
15.生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例:,;计算机也常用十六进制来表示字符代码,它是用0~F来表示0~15,满十六进一,它与十进制对应的数如表:
十进制 0 1 2 … 8 9 10 11 12 13 14 15 16 17 …
十六进制 0 1 2 … 8 9 A B C D E F 10 11 …
例:十六进制2B对应十进制的数为,10C对应十进制的数为,那么十六进制中14E对应十进制的数为 .
16.如图,点E是矩形ABCD边BC上一点,沿AE折叠,点B恰好落在CD边上的点F处,设,
(1)若点F恰为CD边的中点,则x= .
(2)设,则y关于x的函数表达式是 .
三、解答题(共72分,解答应写出必要的演算步骤、文字说明或证明过程)
17.(本题5分)
化简求值:,其中.
18.(本题7分)
如图,在平行四边形ABCD中,,延长AB至点E,使,连接EC.
(1)求证:四边形BECD是矩形.
(2)连接AC,若,,求AC的长.
19.(本题10分)
如图,一次函数的图象与与反比例函数(k≠0,x<0)的图象交于点,B两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积.
20.(本题8分)
某中学举行了心理健康知识测试,为大概了解学生心理健康情况,该校随机抽取了部分学生进行测试,根据成绩(单位:分)分成:,,,五个组,并绘制了如图1和图2所示的统计图.
请根据图中提供的信息,回答下列问题.
(1)本次抽取测试的学生有 人,m= ;
(2)直接补全图1中的统计图,由扇形统计图知E组所占扇形圆心角的度数为 ;
(3)根据调查结果,可估计该校2000名学生中,成绩大于或等于80分的学生约有 人。
(4)学校决定在A组4名学生(3男1女)中随机选取两名学生走进社区进行心理健康知识宣传,求恰好选中一男一女的概率是多少;
21.(本题9分)
如图,在Rt△ADC中,,B是AC上一点,以AB为直径作⊙0,交CD于点E,交AD于点F,连接AE,AE恰好是∠CAD的平分线.
(1)求证:CD是⊙O的切线.
(2)若⊙0的半径为5,,求BC的长.
22.(本题10分)
中国元素几乎遍布卡塔尔世界杯的每一个角落,某特许商品专卖店销售中国制造的纪念品,深受大家喜爱.自世界杯开赛以来,其销量不断增加,该商品销售第x天(,且x为整数)与该天销售量y(件)之间满足函数关系如下表所示:
第x天 1 2 3 4 5 6 7 …
销售量y(件) 220 240 260 280 300 320 340 …
为回馈顾客,该商家将此纪念品的价格不断下调,其销售单价z(元)与第x天(且x为整数)成一次函数关系且满足.已知该纪念品成本价为20元/件.
(1)求y关于x的函数表达式;
(2)求这28天中第几天销售利润最大,并求出最大利润;
(3)商店担心随着世界杯的结束该纪念品的销售情况会不如从前,决定在第20天开始每件商品的单价在原来价格变化的基础上再降价a元销售,销售第x天与该天销售量y(件)仍然满足原来函数关系,问第几天的销售利润取得最大值,若最大利润是20250元,求a的值.
23.(本题11分)
爱动脑筋的小明同学在学习完角平分线的性质一节后意犹未尽经过思考发现里面还有一个有趣的结论:
(1)【问题发现】如图1所示,若AD是∠BAC的角平分线,可得到结论:.
小明的解法如下:
过点D作于点E,于点F,过点A作于点G,
∵AD是∠BAC的角平分线,且,,
∴ ,
,
∵,
∴
(2)【类比探究】如图2所示,若AD是∠BAC的外角平分线,AD与BC的延长线交于点D.求证:
(3)【直接应用】如图3所示,Rt△ABC中,,AD平分∠BAC交BC于D,若,,在不添加辅助线的情况下直接写出 .
(4)【拓展应用】如图4所示,在△ABC中,,,,将△ABC先沿∠BAC的平分线AD折叠,B点刚好落在AC上的E点,剪掉重叠部分(即四边形ABDE),再将余下部分(△CDE)沿∠DEC的平分线EF折叠,再剪掉重叠部分(即四边形DEGF),求出剩余部分△FCG的面积.
24.(本题12分)
二次函数交x轴于点和点,交y轴于点.
(1)求二次函数的解析式;
(2)如图1,点E为抛物线的顶点,点为y轴负半轴上的一点,将抛物线绕点T旋转180°,得到新的抛物线,其中B,E旋转后的对应点分别记为B',E',当四边形BEB'E'的面积为12时,求t的值;
(3)如图2,过点C作轴,交抛物线于另一点D.点M是直线CD上的一个动点,过点M作x轴的垂线,交抛物线于点P.是否存在点M使△PBC为直角三角形,若存在,请直接写出点M的坐标,若不存在,请说明理由.
广水市2023年九年级三月统一考试
数学参考答案
1.D 2.C 3.A 4.C 5.B 6.C 7.D 8.B 9.D 10.C
11.0 12.0 13.26 14. 15.334 16.2
17.(3+2分)
解:,
当时,原式.
18.(3+4分)
(1)证明:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长AB至点E,使BE=AB,
∴BE∥CD,BE=CD,
∴四边形BECD是平行四边形,
∵BD⊥AB,
∴∠DBE=90°,
∴四边形BECD是矩形;
(2)解:
∵四边形ABCD是平行四边形,
∴BC=AD=3,AB=CD=2,
∵四边形BECD是矩形,
∴BE=CD=2,∠BEC=90°,
∴;
∵AB=BE=2,
∴AE=AB+BE=4,
∴.
19.(5+5分)
解:
(1)把A(-2,1)代入y1=x+b得-2+b=1,解得b=3;
把A(-2,1)代入(k≠0,x<0)得k=-2×1=-2,
∴一次函数的表达式是y1=x+3,反比例函数的表达式;
(2)由,解得或,
∴B点坐标为(-1,2),
设直线y=x+3与x轴的交点为C,
把y=0代入求得x=-3,
C(-3,0),
∴.
20.(2+2+2+2分)
(1)40,20
(2)补全图1中统计图,如图所示,
54°
(3)1700
(4)根据题意列表如下:
男1 男2 男3 女
男1 -- 男2男1 男3男1 女男1
男2 男1男2 -- 男3男2 女男2
男3 男1男3 男2男3 -- 女男3
女 男1女 男2女 男3女 --
由表格可知,共有12种等可能的结果,其中选取的2名学生恰好是一男一女的结果有6种,
∴恰好选中一男一女的概率是
21.(5+4分)
(1)连接OE,
∵AE平分∠CAD,
∴∠OAE=∠EAF.
∵AO=EO,
∴∠OAE=∠OEA,
∴∠OEA=∠EAF,
∴OE∥AD.
∵AD⊥CD,
∴OE⊥CD,
∴CD是⊙O的切线;
(2)∵OE∥AD,
∴△CEO △CDA,
∴即,解得.
22.(3+3+4分)
(1)解:由表格信息可得:每增加1天,销量增加20件,可得y是x的一次函数,
设y=kx+b,把x=1,y=220,x=2,y=240代入可得:
,解得:,
∴y关于x的函数表达式为y=20x+200(1≤x≤28);
(2)设总利润为w元,则
;
当时,w取得最大值,
所以,第15天利润最大,最大值为:w=25000(元).
(3)由题意可得:
第20天开始每件商品的单价为元,
每件商品的利润为:元,
设此时利润为:元,则
又∵a=-40<0且20≤x≤28
随x的增大而减小
当x=20时有最大值为20250,
∴,
解得:a=6.25.
综上:第20天时,利润最大为20250元时,此时a=6.25.
23.(2+3+2+4分)
(1)DE=EF
(2)证明:过点D作DN⊥BA于N,过点D作DM⊥AC于M.过点A作AP⊥BD于点P.
∵AD平分∠MAN,
∴DN=DM.
∴,,
∴;
(3)20;
(4)解:
∵∠ABC=90°,AB=6,BC=8,
∴,
∵将△ABC先沿∠BAC的平分线AD折叠,
∴AB=AE=6,∠BAD=∠DAE,∠B=∠AED=90°,BD=DE,
∴EC=4,
由(1)可得,
∴BD=3=DE,DC=5,
∴,
同理可求:,
∴,
∴.
24.(3+4+5分)
(1)解:∵二次函数过点A(-1,0),B(-3,0),
∴设抛物线解析式为y=a(x+1)(x+3),
将C(0,-3)代入,得:3a=-3,
解得:a=-1,
∴二次函数的解析式为:y=-x2-4x-3;
(2)解:
如图1,连接EE′、BB′,延长BE,交y轴于点Q.
由(1)得y=-x2-4x-3=-(x+2)2+1,
∴抛物线顶点E(-2,1),
设直线BE的解析式为y=kx+b,
∵B(-3,0),E(-2,1),
∴,
解得:,
∴直线BE的解析式为:y=x+3,
∴Q(0,3),
∵抛物线y=-x2-4x-3绕点T(0,t)旋转180°,
∴TB=TB′,TE=TE′,
∴四边形BEB′E′是平行四边形,
∴,
∵,
∴TQ=6,
∴3-t=6,
∴t=-3;
(3)解:设P(x,-x2-4x-3),
①如图2,
当∠BP1C=90°时,∠N1P1B=∠P1CE,
∴tan∠N1P1B=tan∠P1CE,
∴,
∵BN1=-x2-4x-3,P1N1=x+3,P1E=-x,EC=-x2-4x,
∴,
化简得:x2+5x+5=0,
解得:,(舍去),
②当∠BP2C=90°时,同理可得:x2+5x+5=0,
解得:(舍去),,
∴M点的坐标为或,
③如图3,
当∠P3BC=90°时,由△BM3C是等腰直角三角形,
∴△N3BP3也是等腰直角三角形,
∴N3B=N3P3,
∴-x2-4x-3=x+3,
化简得:x2+5x+6=0,
解得:x1=-2,x2=-3(舍去),
∴M点的坐标为(-2,-3);
④当∠BCP4=90°时,由△BOC是等腰直角三角形,
可得△N4P4C也是等腰直角三角形,
∴P4N4=CN4,
∴-x=-3-(-x2-4x-3),
化简得:x2+5x=0,
解得:x1=-5,x2=0(舍去),
∴M点的坐标为(-5,-3),
综上所述:
满足条件的M点的坐标为或或(-2,-3)或(-5,-3).
数学试题
(测试时间120分钟 满分120分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卷上,并将准考证号条形码粘贴在答题卷上的指定位置。
2.选择题每小题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答在试题卷上无效。
3.非选择题的作答:用0.5毫米黑色墨水签字笔直接答在答题卷上对应的答题区域内。答在试题卷上无效。
4.考生必须保持答题卷的整洁。考试结束后,请将本试题卷和答题卷一并上交。
一、选择题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,只有一个是正确的)
1.2023的相反数是
A. B. C.2023 D.-2023
2.我国的天问一号火星探测器成功着陆火星,据测算,地球到火星的最近距离约为55000000千米,数据55000000用科学记数法表示为
A. B. C. D.
3.如图,将三角尺的直角顶点放在直尺的一边上,,,则∠3的度数等于
A.20° B.25° C.30° D.35°
4.如图①用一个平面截长方体,得到如图②的几何体,它在我国古代数学名著《九章算术》中被称为堑堵.图②堑堵的俯视图是
A. B. C. D.
5.为了迎接体育中考,体育委员到体育用品商店购买排球和实心球,若购买2个排球和3个实心球共需95元,若购买5个排球和7个实心球共需230元,若设每个排球x元,每个实心球y元,则根据题意列二元一次方程组得
A. B. C. D.
6.在大家跳的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是
A.众数是90 B.中位数是90 C.平均数是90 D.极差是15
7.观察下列尺规作图的痕迹:其中,能够说明的是
A. B. C. D.
8.小明喜欢构建几何图形,利用数形结合的思想解决代数问题.在计算时,如图,在Rt△ACB中,,,延长CB使,连接AD,得,所以,类比小明的方法,计算的值为
A. B. C. D.
9.某村计划挖一条引水渠,渠道的横断面ABCD是一个轴对称图形(如图所示).若渠底宽BC为2m,渠道深BH为3m,渠壁CD的倾角为α,则渠口宽AD为
A. B. C. D.
10.如图,抛物线的对称轴是直线,并与x轴交于A,B两点,若,则下列结论中:①;②;③;④若m为任意实数,则,正确的个数是
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题)
二、填空题(共18分,只需要将结果直接填写在答题卡对应题号处的横线上)
11.计算: .
12.设,是一元二次方程的两根,则 .
13.圆材埋壁是我国古代数学名著《九章算术》中的一个问题:今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?.用现在的几何语言表达即:如图,CD为⊙O的直径,弦,垂足为点E,寸,寸,则直径CD的长度是 寸.
14.如图是用七巧板拼成的正方形桌面,一个小球在桌面上自由地滚动,它最终停在黑色区域的概率是 .
15.生活中常用的十进制是用0~9这十个数字来表示数,满十进一,例:,;计算机也常用十六进制来表示字符代码,它是用0~F来表示0~15,满十六进一,它与十进制对应的数如表:
十进制 0 1 2 … 8 9 10 11 12 13 14 15 16 17 …
十六进制 0 1 2 … 8 9 A B C D E F 10 11 …
例:十六进制2B对应十进制的数为,10C对应十进制的数为,那么十六进制中14E对应十进制的数为 .
16.如图,点E是矩形ABCD边BC上一点,沿AE折叠,点B恰好落在CD边上的点F处,设,
(1)若点F恰为CD边的中点,则x= .
(2)设,则y关于x的函数表达式是 .
三、解答题(共72分,解答应写出必要的演算步骤、文字说明或证明过程)
17.(本题5分)
化简求值:,其中.
18.(本题7分)
如图,在平行四边形ABCD中,,延长AB至点E,使,连接EC.
(1)求证:四边形BECD是矩形.
(2)连接AC,若,,求AC的长.
19.(本题10分)
如图,一次函数的图象与与反比例函数(k≠0,x<0)的图象交于点,B两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积.
20.(本题8分)
某中学举行了心理健康知识测试,为大概了解学生心理健康情况,该校随机抽取了部分学生进行测试,根据成绩(单位:分)分成:,,,五个组,并绘制了如图1和图2所示的统计图.
请根据图中提供的信息,回答下列问题.
(1)本次抽取测试的学生有 人,m= ;
(2)直接补全图1中的统计图,由扇形统计图知E组所占扇形圆心角的度数为 ;
(3)根据调查结果,可估计该校2000名学生中,成绩大于或等于80分的学生约有 人。
(4)学校决定在A组4名学生(3男1女)中随机选取两名学生走进社区进行心理健康知识宣传,求恰好选中一男一女的概率是多少;
21.(本题9分)
如图,在Rt△ADC中,,B是AC上一点,以AB为直径作⊙0,交CD于点E,交AD于点F,连接AE,AE恰好是∠CAD的平分线.
(1)求证:CD是⊙O的切线.
(2)若⊙0的半径为5,,求BC的长.
22.(本题10分)
中国元素几乎遍布卡塔尔世界杯的每一个角落,某特许商品专卖店销售中国制造的纪念品,深受大家喜爱.自世界杯开赛以来,其销量不断增加,该商品销售第x天(,且x为整数)与该天销售量y(件)之间满足函数关系如下表所示:
第x天 1 2 3 4 5 6 7 …
销售量y(件) 220 240 260 280 300 320 340 …
为回馈顾客,该商家将此纪念品的价格不断下调,其销售单价z(元)与第x天(且x为整数)成一次函数关系且满足.已知该纪念品成本价为20元/件.
(1)求y关于x的函数表达式;
(2)求这28天中第几天销售利润最大,并求出最大利润;
(3)商店担心随着世界杯的结束该纪念品的销售情况会不如从前,决定在第20天开始每件商品的单价在原来价格变化的基础上再降价a元销售,销售第x天与该天销售量y(件)仍然满足原来函数关系,问第几天的销售利润取得最大值,若最大利润是20250元,求a的值.
23.(本题11分)
爱动脑筋的小明同学在学习完角平分线的性质一节后意犹未尽经过思考发现里面还有一个有趣的结论:
(1)【问题发现】如图1所示,若AD是∠BAC的角平分线,可得到结论:.
小明的解法如下:
过点D作于点E,于点F,过点A作于点G,
∵AD是∠BAC的角平分线,且,,
∴ ,
,
∵,
∴
(2)【类比探究】如图2所示,若AD是∠BAC的外角平分线,AD与BC的延长线交于点D.求证:
(3)【直接应用】如图3所示,Rt△ABC中,,AD平分∠BAC交BC于D,若,,在不添加辅助线的情况下直接写出 .
(4)【拓展应用】如图4所示,在△ABC中,,,,将△ABC先沿∠BAC的平分线AD折叠,B点刚好落在AC上的E点,剪掉重叠部分(即四边形ABDE),再将余下部分(△CDE)沿∠DEC的平分线EF折叠,再剪掉重叠部分(即四边形DEGF),求出剩余部分△FCG的面积.
24.(本题12分)
二次函数交x轴于点和点,交y轴于点.
(1)求二次函数的解析式;
(2)如图1,点E为抛物线的顶点,点为y轴负半轴上的一点,将抛物线绕点T旋转180°,得到新的抛物线,其中B,E旋转后的对应点分别记为B',E',当四边形BEB'E'的面积为12时,求t的值;
(3)如图2,过点C作轴,交抛物线于另一点D.点M是直线CD上的一个动点,过点M作x轴的垂线,交抛物线于点P.是否存在点M使△PBC为直角三角形,若存在,请直接写出点M的坐标,若不存在,请说明理由.
广水市2023年九年级三月统一考试
数学参考答案
1.D 2.C 3.A 4.C 5.B 6.C 7.D 8.B 9.D 10.C
11.0 12.0 13.26 14. 15.334 16.2
17.(3+2分)
解:,
当时,原式.
18.(3+4分)
(1)证明:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵延长AB至点E,使BE=AB,
∴BE∥CD,BE=CD,
∴四边形BECD是平行四边形,
∵BD⊥AB,
∴∠DBE=90°,
∴四边形BECD是矩形;
(2)解:
∵四边形ABCD是平行四边形,
∴BC=AD=3,AB=CD=2,
∵四边形BECD是矩形,
∴BE=CD=2,∠BEC=90°,
∴;
∵AB=BE=2,
∴AE=AB+BE=4,
∴.
19.(5+5分)
解:
(1)把A(-2,1)代入y1=x+b得-2+b=1,解得b=3;
把A(-2,1)代入(k≠0,x<0)得k=-2×1=-2,
∴一次函数的表达式是y1=x+3,反比例函数的表达式;
(2)由,解得或,
∴B点坐标为(-1,2),
设直线y=x+3与x轴的交点为C,
把y=0代入求得x=-3,
C(-3,0),
∴.
20.(2+2+2+2分)
(1)40,20
(2)补全图1中统计图,如图所示,
54°
(3)1700
(4)根据题意列表如下:
男1 男2 男3 女
男1 -- 男2男1 男3男1 女男1
男2 男1男2 -- 男3男2 女男2
男3 男1男3 男2男3 -- 女男3
女 男1女 男2女 男3女 --
由表格可知,共有12种等可能的结果,其中选取的2名学生恰好是一男一女的结果有6种,
∴恰好选中一男一女的概率是
21.(5+4分)
(1)连接OE,
∵AE平分∠CAD,
∴∠OAE=∠EAF.
∵AO=EO,
∴∠OAE=∠OEA,
∴∠OEA=∠EAF,
∴OE∥AD.
∵AD⊥CD,
∴OE⊥CD,
∴CD是⊙O的切线;
(2)∵OE∥AD,
∴△CEO △CDA,
∴即,解得.
22.(3+3+4分)
(1)解:由表格信息可得:每增加1天,销量增加20件,可得y是x的一次函数,
设y=kx+b,把x=1,y=220,x=2,y=240代入可得:
,解得:,
∴y关于x的函数表达式为y=20x+200(1≤x≤28);
(2)设总利润为w元,则
;
当时,w取得最大值,
所以,第15天利润最大,最大值为:w=25000(元).
(3)由题意可得:
第20天开始每件商品的单价为元,
每件商品的利润为:元,
设此时利润为:元,则
又∵a=-40<0且20≤x≤28
随x的增大而减小
当x=20时有最大值为20250,
∴,
解得:a=6.25.
综上:第20天时,利润最大为20250元时,此时a=6.25.
23.(2+3+2+4分)
(1)DE=EF
(2)证明:过点D作DN⊥BA于N,过点D作DM⊥AC于M.过点A作AP⊥BD于点P.
∵AD平分∠MAN,
∴DN=DM.
∴,,
∴;
(3)20;
(4)解:
∵∠ABC=90°,AB=6,BC=8,
∴,
∵将△ABC先沿∠BAC的平分线AD折叠,
∴AB=AE=6,∠BAD=∠DAE,∠B=∠AED=90°,BD=DE,
∴EC=4,
由(1)可得,
∴BD=3=DE,DC=5,
∴,
同理可求:,
∴,
∴.
24.(3+4+5分)
(1)解:∵二次函数过点A(-1,0),B(-3,0),
∴设抛物线解析式为y=a(x+1)(x+3),
将C(0,-3)代入,得:3a=-3,
解得:a=-1,
∴二次函数的解析式为:y=-x2-4x-3;
(2)解:
如图1,连接EE′、BB′,延长BE,交y轴于点Q.
由(1)得y=-x2-4x-3=-(x+2)2+1,
∴抛物线顶点E(-2,1),
设直线BE的解析式为y=kx+b,
∵B(-3,0),E(-2,1),
∴,
解得:,
∴直线BE的解析式为:y=x+3,
∴Q(0,3),
∵抛物线y=-x2-4x-3绕点T(0,t)旋转180°,
∴TB=TB′,TE=TE′,
∴四边形BEB′E′是平行四边形,
∴,
∵,
∴TQ=6,
∴3-t=6,
∴t=-3;
(3)解:设P(x,-x2-4x-3),
①如图2,
当∠BP1C=90°时,∠N1P1B=∠P1CE,
∴tan∠N1P1B=tan∠P1CE,
∴,
∵BN1=-x2-4x-3,P1N1=x+3,P1E=-x,EC=-x2-4x,
∴,
化简得:x2+5x+5=0,
解得:,(舍去),
②当∠BP2C=90°时,同理可得:x2+5x+5=0,
解得:(舍去),,
∴M点的坐标为或,
③如图3,
当∠P3BC=90°时,由△BM3C是等腰直角三角形,
∴△N3BP3也是等腰直角三角形,
∴N3B=N3P3,
∴-x2-4x-3=x+3,
化简得:x2+5x+6=0,
解得:x1=-2,x2=-3(舍去),
∴M点的坐标为(-2,-3);
④当∠BCP4=90°时,由△BOC是等腰直角三角形,
可得△N4P4C也是等腰直角三角形,
∴P4N4=CN4,
∴-x=-3-(-x2-4x-3),
化简得:x2+5x=0,
解得:x1=-5,x2=0(舍去),
∴M点的坐标为(-5,-3),
综上所述:
满足条件的M点的坐标为或或(-2,-3)或(-5,-3).
同课章节目录
