北京2022-2023学年九年级数学统测 试卷(含答案)
文档属性
| 名称 | 北京2022-2023学年九年级数学统测 试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 847.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 00:00:00 | ||
图片预览


文档简介
北师大2022-2023学年初三下数学测试6
一、选择题(共16分,每题2分)
1.下列四家银行的标志中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
2.在学习强国平台中,5月16日发布的“第一观察——天问落火”栏目的阅读量截止到5月17日中午,就已经达到了10895538人次,将10895538精确到万,得( )
A.1089 B.1090 C.1089万 D.1090万
3.实数a,b在数轴上对应的点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
4.学校图书馆的阅读角有一块半径为,圆心角为的扇形地毯,这块地毯的面积为( )
A. B. C. D.
5.如图,已知,那么的度数为( )
A. B. C. D.
6.不透明的袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次摸到相同颜色的小球的概率是( )
A. B. C. D.
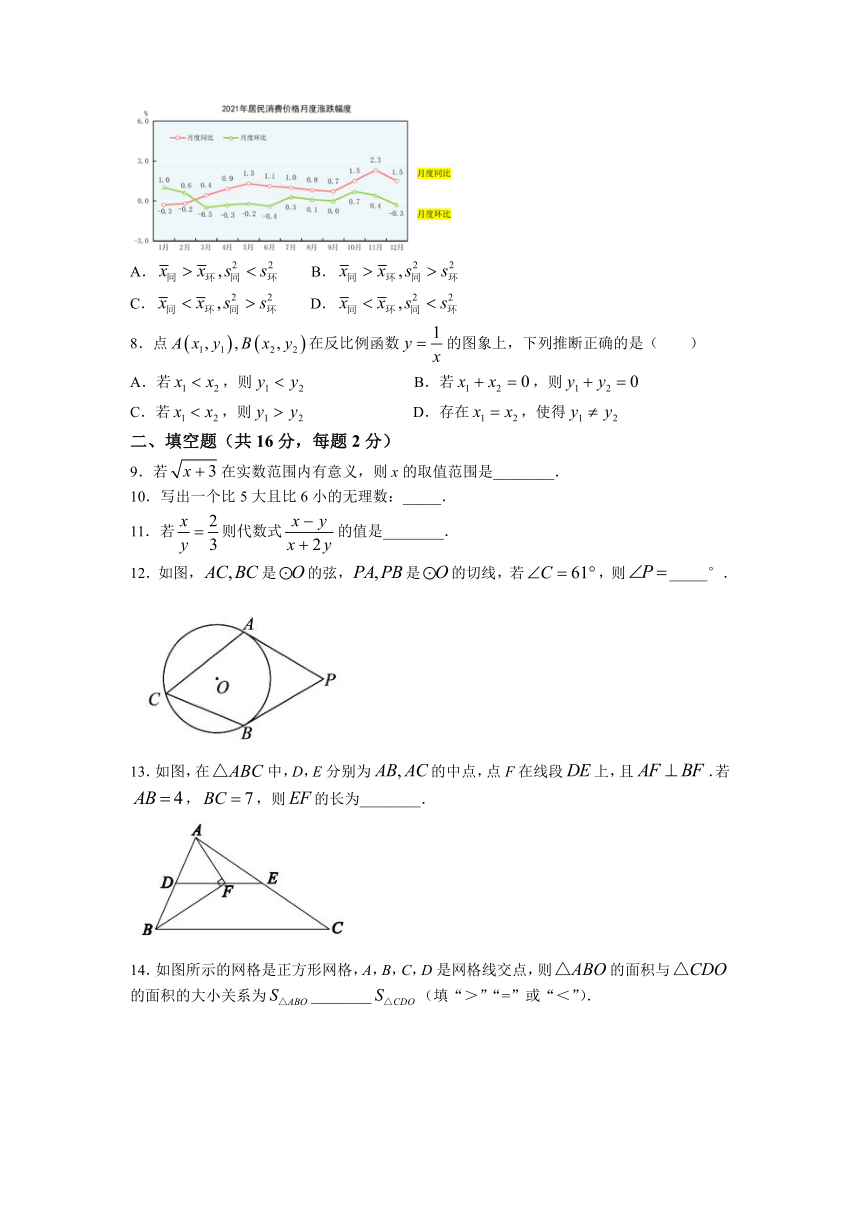
7.下图是国家统计局公布的2021年居民消费价格月度涨跌幅度,月度同比和月度环比的平均数分别为,方差分别为,则( )
A. B.
C. D.
8.点在反比例函数的图象上,下列推断正确的是( )
A.若,则 B.若,则
C.若,则 D.存在,使得
二、填空题(共16分,每题2分)
9.若在实数范围内有意义,则x的取值范围是________.
10.写出一个比5大且比6小的无理数:_____.
11.若则代数式的值是________.
12.如图,是的弦,是的切线,若,则_____°.
13.如图,在中,D,E分别为的中点,点F在线段上,且.若,,则的长为________.
14.如图所示的网格是正方形网格,A,B,C,D是网格线交点,则的面积与的面积的大小关系为________(填“>”“=”或“<”).
15.若关于x的一元二次方程有一个根是,则__________.
16.尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:
演员1 演员2 演员3 演员4 演员5 演员6 演员7 演员8
节目A √ √ √ √ √
节目B √ √ √
节目C √ √ √
节目D √ √
节目E √ √
节目F √ √
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,首尾两个节目分别是A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后顺序_________(只需按演出顺序填写中间4个节目的字母即可).
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:
18.解不等式组并写出它的非负整数解.
19.已知关于x的一元二次方程有两个不相等的实数根.
(1)求m的取值范围;
(2)若方程有一个根是0,求方程的另一个根.
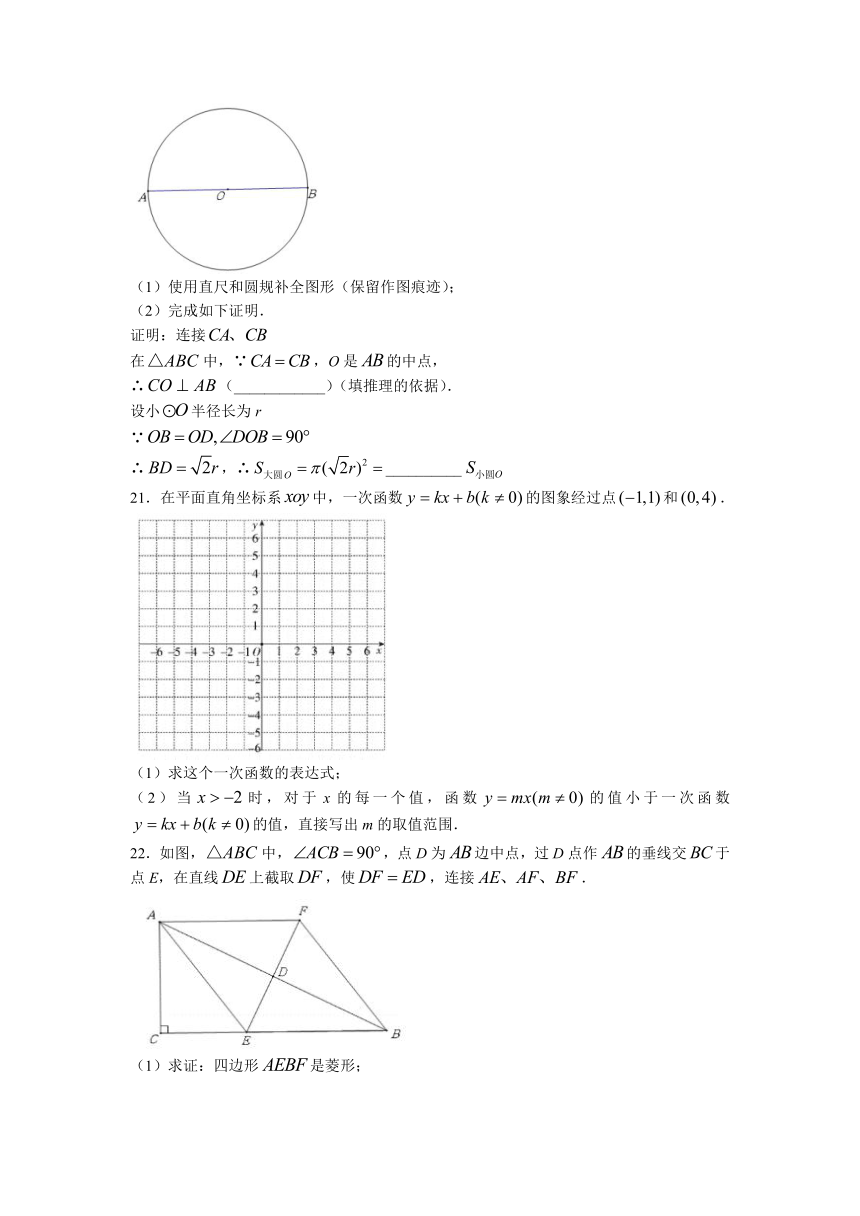
20.有趣的倍圆问题:校园里有个圆形花坛,春季改造,负责该片花园维护的某班同学经过协商,想把该花坛的面积扩大一倍,他们在图纸上设计了以下施工方案:
①在中作直径,分别以A、B为圆心,大于二分之一长为半径画弧,两弧在直径上方交于点C,作射线交于点D;
②连接,以O为圆心长为半径画圆;
③大即为所求作.
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成如下证明.
证明:连接
在中,∵,O是的中点,
∴(____________)(填推理的依据).
设小半径长为r
∵
∴,∴__________
21.在平面直角坐标系中,一次函数的图象经过点和.
(1)求这个一次函数的表达式;
(2)当时,对于x的每一个值,函数的值小于一次函数的值,直接写出m的取值范围.
22.如图,中,,点D为边中点,过D点作的垂线交于点E,在直线上截取,使,连接.
(1)求证:四边形是菱形;
(2)若,连接,求的长.
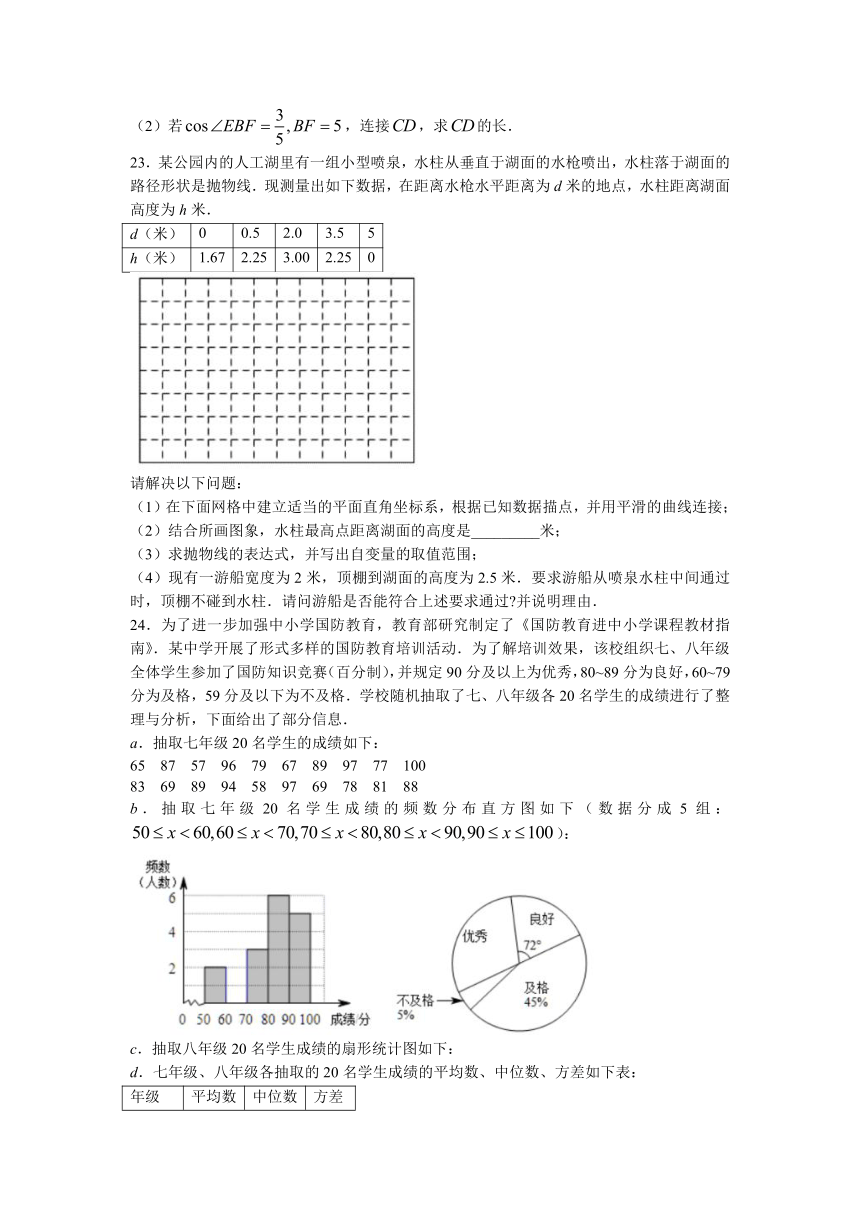
23.某公园内的人工湖里有一组小型喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距离水枪水平距离为d米的地点,水柱距离湖面高度为h米.
d(米) 0 0.5 2.0 3.5 5
h(米) 1.67 2.25 3.00 2.25 0
请解决以下问题:
(1)在下面网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
(2)结合所画图象,水柱最高点距离湖面的高度是_________米;
(3)求抛物线的表达式,并写出自变量的取值范围;
(4)现有一游船宽度为2米,顶棚到湖面的高度为2.5米.要求游船从喷泉水柱中间通过时,顶棚不碰到水柱.请问游船是否能符合上述要求通过 并说明理由.
24.为了进一步加强中小学国防教育,教育部研究制定了《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织七、八年级全体学生参加了国防知识竞赛(百分制),并规定90分及以上为优秀,80~89分为良好,60~79分为及格,59分及以下为不及格.学校随机抽取了七、八年级各20名学生的成绩进行了整理与分析,下面给出了部分信息.
a.抽取七年级20名学生的成绩如下:
65 87 57 96 79 67 89 97 77 100
83 69 89 94 58 97 69 78 81 88
b.抽取七年级20名学生成绩的频数分布直方图如下(数据分成5组:):
c.抽取八年级20名学生成绩的扇形统计图如下:
d.七年级、八年级各抽取的20名学生成绩的平均数、中位数、方差如下表:
年级 平均数 中位数 方差
七年级 81 m 167.9
八年级 82 81 108.3
请根据以上信息,回答下列问题:
(1)补全七年级20名学生成绩的频数分布直方图,写出表中m的值;
(2)该校目前七年级有学生300人,八年级有学生200人,估计两个年级此次测试成绩达到优秀的学生各有多少人?
(3)你认为哪个年级的学生成绩较好,并说明理由.
25.如图,在中,,以为直径的与边相交于点D,与边相交于点F,,垂足为点E,连接.
(1)求证:与相切;
(2)若,,求的长.
26.在平面直角坐标系中,点在抛物线上.
(1)若,求的值;
(2)若,求的取值范围.
27.在中,,过点C作射线,使(点与点B在直线的异侧),点D是射线上一个动点(不与点C重合),点E在线段上,且.
(1)如图1,当点E与点C重合时,与的位置关系是________,若,则的长为________;(用含a的式子表示)
(2)如图2,当点E与点C不重合时,连接.
①用等式表示与之间的数量关系,并证明;
②用等式表示线段之间的数量关系,并证明.
28.在平面直角坐标系中,对于直线,给出如下定义:若直线l与某个圆相交,则两个交点之间的距离称为直线l关于该圆的“圆截距”.
(1)如图1,的半径为1,当时,直接写出直线l关于的“圆截距”;
(2)点M的坐标为,
①如图2,若的半径为1,当时,直线l关于的“圆截距”小于,求k的取值范围;
②如图3,若的半径为2,当k的取值在实数范围内变化时,直线l关于的“圆截距”的最小值为,直接写出b的值.
数学统测6答案
一、选择题(每小题2分,共16分)
1 2 3 4 5 6 7 8
B D C C B A B B
二、填空题(每小题2分,共16分)
9、; 10、例如;答案不唯一 11、 12、58;
13、1.5; 14、=; 15、1; 16、DBEC或DCEB.
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)
17.解:
18.解,得;
解,得,
∴不等式组的解集是,
∴非负整数解是0,1.
19解:(1)∵关于x的一元二次方程有两个不相等的实数根
∴且
∴,且
(2)∵此方程有一个根是0,
∴,
∴.
∴此方程为.
∴方程的另一根为.
20.(1)尺规作图
(2)三线合一
2
21.(1)∵一次函数的图象经过点和
∴
∴
∴
(2)直线 当时,
当过点时,
当与直线平行时,
∴时结论成立.
22.(1)证明:
∵
∴四边形是平行四边形
∵
∴四边形是菱形
(2)∵四边形是菱形
∴
∴
∵
∴
在中,∵,∴,
∴,
∵
∴
在中,∵,D为中点
∴
23.解:(1)
(2)3米
(3)由数据可知,抛物线的顶点坐标为,且过点
设抛物线的表达式为
∴
将点代入,得
∴抛物线的表达式为
自变量的取值范围是
(4)游船能通过.
理由如下:当和时,,而游船宽2米,顶棚到湖面的高为2.5米,所以游船从距离水枪水平距离为1米处通过时,顶棚不会碰到水柱.
24.解:(1)补全频数分布直方图如下
表中m的值为82
(2)此次七年级测试成绩达到优秀的学生为(人)
抽取八年级20名学生成绩的优秀率为
此次八年级测试成绩达到优秀的学生为(人)
(3)八年级的学生成绩较好.
理由是:抽取的八年级20名学生的平均成绩为82,高于七年级,两个年级的中位数接近,且八年级的学生成绩的方差小.
25.(1)证明:∵
∴
∵
∴
∵
∴
∴
∴
∴
∴
又∵为半径
∴是的切线.
(2)过O作于H
∵
∴
∵矩形
∴
∴
∴
26.解:(1)∵,
∴抛物线对称轴为y轴.
∵关于y轴对称,
∴.
(2)把代入,得.
∴.
把代入,得.
由题意可知抛物线开口向下且经过点,对称轴为.
∵,
∴.
∵,
∴.
综上,.
∴.
即.
27.解:(1),;
(2)①.
证明:∵,
∴.
∴.
∵,,
∴.
∴.
②.
证明:作,交射线于点F,如图,
则.
∵,
∴.
∴,
即.
∵,,
∴.
∵,
∴.
∴,.
∵,
∴.
∴.
∴.
∴.
28.解:(1).
(2)①如图,当直线l经过点时,.
可知.
∴.
∴.
设与的另一个交点为C,连接,可知.
∴.
即此时直线l关于的“圆截距”为.
结合图形可知.
如图,当直线l经过点时,.
由对称性可得,此时直线l关于的“圆截距”为.
结合图形可知.
综上,当或时直线l关于的“圆截距”小于.
②.
一、选择题(共16分,每题2分)
1.下列四家银行的标志中,是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
2.在学习强国平台中,5月16日发布的“第一观察——天问落火”栏目的阅读量截止到5月17日中午,就已经达到了10895538人次,将10895538精确到万,得( )
A.1089 B.1090 C.1089万 D.1090万
3.实数a,b在数轴上对应的点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
4.学校图书馆的阅读角有一块半径为,圆心角为的扇形地毯,这块地毯的面积为( )
A. B. C. D.
5.如图,已知,那么的度数为( )
A. B. C. D.
6.不透明的袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次摸到相同颜色的小球的概率是( )
A. B. C. D.
7.下图是国家统计局公布的2021年居民消费价格月度涨跌幅度,月度同比和月度环比的平均数分别为,方差分别为,则( )
A. B.
C. D.
8.点在反比例函数的图象上,下列推断正确的是( )
A.若,则 B.若,则
C.若,则 D.存在,使得
二、填空题(共16分,每题2分)
9.若在实数范围内有意义,则x的取值范围是________.
10.写出一个比5大且比6小的无理数:_____.
11.若则代数式的值是________.
12.如图,是的弦,是的切线,若,则_____°.
13.如图,在中,D,E分别为的中点,点F在线段上,且.若,,则的长为________.
14.如图所示的网格是正方形网格,A,B,C,D是网格线交点,则的面积与的面积的大小关系为________(填“>”“=”或“<”).
15.若关于x的一元二次方程有一个根是,则__________.
16.尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:
演员1 演员2 演员3 演员4 演员5 演员6 演员7 演员8
节目A √ √ √ √ √
节目B √ √ √
节目C √ √ √
节目D √ √
节目E √ √
节目F √ √
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,首尾两个节目分别是A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后顺序_________(只需按演出顺序填写中间4个节目的字母即可).
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.
17.计算:
18.解不等式组并写出它的非负整数解.
19.已知关于x的一元二次方程有两个不相等的实数根.
(1)求m的取值范围;
(2)若方程有一个根是0,求方程的另一个根.
20.有趣的倍圆问题:校园里有个圆形花坛,春季改造,负责该片花园维护的某班同学经过协商,想把该花坛的面积扩大一倍,他们在图纸上设计了以下施工方案:
①在中作直径,分别以A、B为圆心,大于二分之一长为半径画弧,两弧在直径上方交于点C,作射线交于点D;
②连接,以O为圆心长为半径画圆;
③大即为所求作.
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成如下证明.
证明:连接
在中,∵,O是的中点,
∴(____________)(填推理的依据).
设小半径长为r
∵
∴,∴__________
21.在平面直角坐标系中,一次函数的图象经过点和.
(1)求这个一次函数的表达式;
(2)当时,对于x的每一个值,函数的值小于一次函数的值,直接写出m的取值范围.
22.如图,中,,点D为边中点,过D点作的垂线交于点E,在直线上截取,使,连接.
(1)求证:四边形是菱形;
(2)若,连接,求的长.
23.某公园内的人工湖里有一组小型喷泉,水柱从垂直于湖面的水枪喷出,水柱落于湖面的路径形状是抛物线.现测量出如下数据,在距离水枪水平距离为d米的地点,水柱距离湖面高度为h米.
d(米) 0 0.5 2.0 3.5 5
h(米) 1.67 2.25 3.00 2.25 0
请解决以下问题:
(1)在下面网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
(2)结合所画图象,水柱最高点距离湖面的高度是_________米;
(3)求抛物线的表达式,并写出自变量的取值范围;
(4)现有一游船宽度为2米,顶棚到湖面的高度为2.5米.要求游船从喷泉水柱中间通过时,顶棚不碰到水柱.请问游船是否能符合上述要求通过 并说明理由.
24.为了进一步加强中小学国防教育,教育部研究制定了《国防教育进中小学课程教材指南》.某中学开展了形式多样的国防教育培训活动.为了解培训效果,该校组织七、八年级全体学生参加了国防知识竞赛(百分制),并规定90分及以上为优秀,80~89分为良好,60~79分为及格,59分及以下为不及格.学校随机抽取了七、八年级各20名学生的成绩进行了整理与分析,下面给出了部分信息.
a.抽取七年级20名学生的成绩如下:
65 87 57 96 79 67 89 97 77 100
83 69 89 94 58 97 69 78 81 88
b.抽取七年级20名学生成绩的频数分布直方图如下(数据分成5组:):
c.抽取八年级20名学生成绩的扇形统计图如下:
d.七年级、八年级各抽取的20名学生成绩的平均数、中位数、方差如下表:
年级 平均数 中位数 方差
七年级 81 m 167.9
八年级 82 81 108.3
请根据以上信息,回答下列问题:
(1)补全七年级20名学生成绩的频数分布直方图,写出表中m的值;
(2)该校目前七年级有学生300人,八年级有学生200人,估计两个年级此次测试成绩达到优秀的学生各有多少人?
(3)你认为哪个年级的学生成绩较好,并说明理由.
25.如图,在中,,以为直径的与边相交于点D,与边相交于点F,,垂足为点E,连接.
(1)求证:与相切;
(2)若,,求的长.
26.在平面直角坐标系中,点在抛物线上.
(1)若,求的值;
(2)若,求的取值范围.
27.在中,,过点C作射线,使(点与点B在直线的异侧),点D是射线上一个动点(不与点C重合),点E在线段上,且.
(1)如图1,当点E与点C重合时,与的位置关系是________,若,则的长为________;(用含a的式子表示)
(2)如图2,当点E与点C不重合时,连接.
①用等式表示与之间的数量关系,并证明;
②用等式表示线段之间的数量关系,并证明.
28.在平面直角坐标系中,对于直线,给出如下定义:若直线l与某个圆相交,则两个交点之间的距离称为直线l关于该圆的“圆截距”.
(1)如图1,的半径为1,当时,直接写出直线l关于的“圆截距”;
(2)点M的坐标为,
①如图2,若的半径为1,当时,直线l关于的“圆截距”小于,求k的取值范围;
②如图3,若的半径为2,当k的取值在实数范围内变化时,直线l关于的“圆截距”的最小值为,直接写出b的值.
数学统测6答案
一、选择题(每小题2分,共16分)
1 2 3 4 5 6 7 8
B D C C B A B B
二、填空题(每小题2分,共16分)
9、; 10、例如;答案不唯一 11、 12、58;
13、1.5; 14、=; 15、1; 16、DBEC或DCEB.
三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题6分,第27-28题,每小题7分)
17.解:
18.解,得;
解,得,
∴不等式组的解集是,
∴非负整数解是0,1.
19解:(1)∵关于x的一元二次方程有两个不相等的实数根
∴且
∴,且
(2)∵此方程有一个根是0,
∴,
∴.
∴此方程为.
∴方程的另一根为.
20.(1)尺规作图
(2)三线合一
2
21.(1)∵一次函数的图象经过点和
∴
∴
∴
(2)直线 当时,
当过点时,
当与直线平行时,
∴时结论成立.
22.(1)证明:
∵
∴四边形是平行四边形
∵
∴四边形是菱形
(2)∵四边形是菱形
∴
∴
∵
∴
在中,∵,∴,
∴,
∵
∴
在中,∵,D为中点
∴
23.解:(1)
(2)3米
(3)由数据可知,抛物线的顶点坐标为,且过点
设抛物线的表达式为
∴
将点代入,得
∴抛物线的表达式为
自变量的取值范围是
(4)游船能通过.
理由如下:当和时,,而游船宽2米,顶棚到湖面的高为2.5米,所以游船从距离水枪水平距离为1米处通过时,顶棚不会碰到水柱.
24.解:(1)补全频数分布直方图如下
表中m的值为82
(2)此次七年级测试成绩达到优秀的学生为(人)
抽取八年级20名学生成绩的优秀率为
此次八年级测试成绩达到优秀的学生为(人)
(3)八年级的学生成绩较好.
理由是:抽取的八年级20名学生的平均成绩为82,高于七年级,两个年级的中位数接近,且八年级的学生成绩的方差小.
25.(1)证明:∵
∴
∵
∴
∵
∴
∴
∴
∴
∴
又∵为半径
∴是的切线.
(2)过O作于H
∵
∴
∵矩形
∴
∴
∴
26.解:(1)∵,
∴抛物线对称轴为y轴.
∵关于y轴对称,
∴.
(2)把代入,得.
∴.
把代入,得.
由题意可知抛物线开口向下且经过点,对称轴为.
∵,
∴.
∵,
∴.
综上,.
∴.
即.
27.解:(1),;
(2)①.
证明:∵,
∴.
∴.
∵,,
∴.
∴.
②.
证明:作,交射线于点F,如图,
则.
∵,
∴.
∴,
即.
∵,,
∴.
∵,
∴.
∴,.
∵,
∴.
∴.
∴.
∴.
28.解:(1).
(2)①如图,当直线l经过点时,.
可知.
∴.
∴.
设与的另一个交点为C,连接,可知.
∴.
即此时直线l关于的“圆截距”为.
结合图形可知.
如图,当直线l经过点时,.
由对称性可得,此时直线l关于的“圆截距”为.
结合图形可知.
综上,当或时直线l关于的“圆截距”小于.
②.
同课章节目录
