5.3反比例函数复习 课件27张
图片预览






文档简介
课件27张PPT。复习反比例函数 反比例函数表达式的确定、反比例函数的图像和性质、反比例函数图像与一次函数图像的关系、利用反比例函数解决问题等都是中考的重要考点。复习指导:1.反比例函数:一般地,如果两个变量x、y之间的关系可以表示
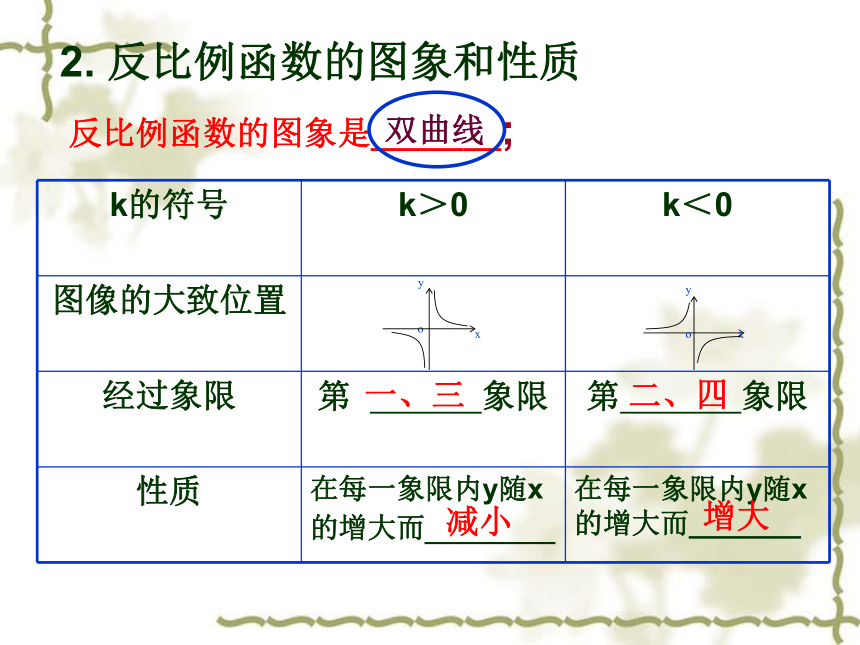
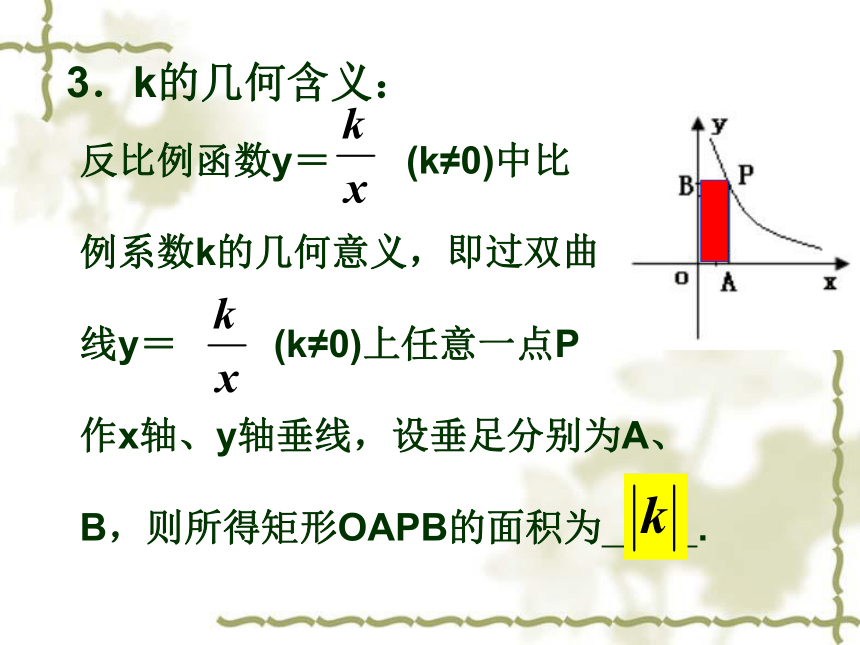
成y= 或 或 (k为常数,k≠0)的形式,那么称y是x的反比例函数. 考点链接:y=kx-1k=xy反比例函数的图象是_______; 2. 反比例函数的图象和性质一、三二、四减小增大双曲线3.k的几何含义:反比例函数y= (k≠0)中比
例系数k的几何意义,即过双曲
线y= (k≠0)上任意一点P
作x轴、y轴垂线,设垂足分别为A、
B,则所得矩形OAPB的面积为 .例1:(柳州)反比例函数
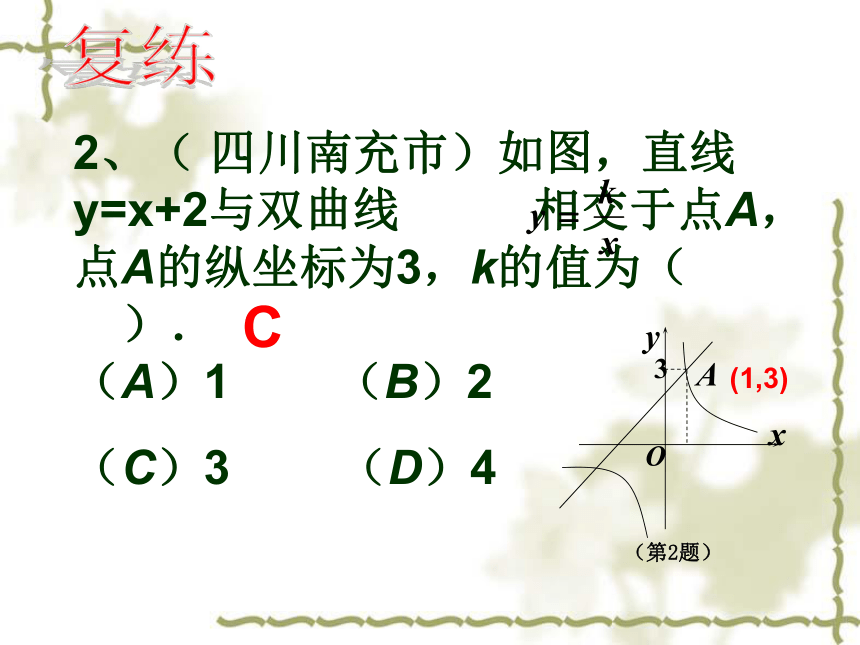
的图象经过点(2,1),则的值m是 . 考点剖析:1、反比例函数的概念11.( 广西钦州市)反比例函数 (k >0)的图象与经过原点的直线L相交于A、B两点,已知A点的坐标为(2,1),那么B点的坐标为 .复练(-2,-1)2、( 四川南充市)如图,直线 y=x+2与双曲线 相交于点A,点A的纵坐标为3,k的值为( ). (A)1 (B)2
(C)3 (D)4复练C(1,3)例2:( 常州)若反比例函数的图象在其每个象限内,y随x的增大而减小,
则k的值可以是( )
A.-1 B.3 C.0 D.-32、反比例函数的图象和性质B 例3:( 新疆)在函数的图象 上有
三个点的坐标分别为(1, )( , )
( -3, ),函数值 的
大小关系是( )D1、已知反比例函数,其图象所在的每个象限内随着的增大而增大,请写出一个符合条件的反比例函数关系式:复练2、 已知点(-1, ),(2, ),(3, )在反比例函数 的图象上. 下列结论中正确的是( )B复练3、反比例函数的关系式D例5:( 天津)已知图中的曲线是反比例函数 (m为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数m的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数 的图象在第一象内限的交点为A,过A点作轴的垂线,垂足为B,当 的面积为4时,求点A的坐标及反比例函数的解析式.解:(Ⅰ)这个反比例函数图象的另一支在第三象限.
因为这个反比例函数的图象分布在第一、第三象限,
所以m-5>0,解得m>5. (Ⅱ)如图,由第一象限内的点A在正比例函数y=2x的图象上,
设点A的坐标为(a,2a) (a>0),
则点B的坐标为(a,0),
解得a=2(负值舍去).
A点的坐标为(2,4).
又点A在反比例函数 的图象上, ,即:m-5=8
所以反比例函数的解析式为 .1、( 江苏淮安)若一次函数y=2x+l的图象与反比例函数图象的一个交点横坐标为l,则反比例函数关系式为 .复练2、( 山西)如图,A是反比例函数图象上一点,过点A作轴于点B,点P在x轴上,△ABP面积为2,则这个反比例函数的解析式为 。复练复练3.( 安徽省中中考) 点P(1,a)在反比例函数 的图象上,它关于轴的对称点在一次函数 y=2x+4 的图象上,求此反比例函数的解析式。例6:( 安徽)一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )4、反比例函数的实际应用A1.( 重庆綦江县)有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 (单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=2m3时,气体的密度是_______kg/m3.复练4复练2.( 浙江嘉兴)一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系: ,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).
(1)求k和m的值;
(2)若行驶速度不得超过
60(km/h),则汽车通过
该路段最少需要多少时间?解:(1)将A(40,1)代入 ,解得 k=40 .
函数解析式为:
当t=0.5时,解得m=80
所以,k=40 , m=80 .
(2)令v=60,得.
结合函数图象可知,汽车通过该路段最少需要 小时. 5、反比例函数的综合运用例7.( 北京)已知反比例函数 的图像经过点A( ,1)
(1)试确定此反比例函数的解析式.
(2)点O是坐标原点,将线段OA绕点O顺时针旋转30°得到线段OB,判断点B是否在反比例函数的图像上,并说明理由.
(3)已知点P(m, )也在此反比例函数的图像上(其中m <0),过p点作x轴的的垂线,交x轴于点M,若线段PM上存在一点Q,使得△OQM的面积是 ,设Q点的纵坐标为n,求 的值.1、( 温州)如图,在平面直角坐标系中,直线AB与Y轴和X轴分别交于点A、点B,与反比例函数 在第一象限的图象交于点c(1,6)、点D(3,y).过点C作CE上y轴于E,过点D作DF上X轴于F.
(1)求m,n的值;
(2)求直线AB的函数解析式;
(3)求证:△AEC∽△DFB.复练2、( 兰州)如图,已知,
A(-4,n),B(2,-4)是一次函数 的图象和反比例函数 的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与X轴的交点C的坐标及△AOB的面积;
(3)求 方程的解(请直接写出答案);
(4)求 不等式的解集(请直接写出答案).复练y=-x-2
成y= 或 或 (k为常数,k≠0)的形式,那么称y是x的反比例函数. 考点链接:y=kx-1k=xy反比例函数的图象是_______; 2. 反比例函数的图象和性质一、三二、四减小增大双曲线3.k的几何含义:反比例函数y= (k≠0)中比
例系数k的几何意义,即过双曲
线y= (k≠0)上任意一点P
作x轴、y轴垂线,设垂足分别为A、
B,则所得矩形OAPB的面积为 .例1:(柳州)反比例函数
的图象经过点(2,1),则的值m是 . 考点剖析:1、反比例函数的概念11.( 广西钦州市)反比例函数 (k >0)的图象与经过原点的直线L相交于A、B两点,已知A点的坐标为(2,1),那么B点的坐标为 .复练(-2,-1)2、( 四川南充市)如图,直线 y=x+2与双曲线 相交于点A,点A的纵坐标为3,k的值为( ). (A)1 (B)2
(C)3 (D)4复练C(1,3)例2:( 常州)若反比例函数的图象在其每个象限内,y随x的增大而减小,
则k的值可以是( )
A.-1 B.3 C.0 D.-32、反比例函数的图象和性质B 例3:( 新疆)在函数的图象 上有
三个点的坐标分别为(1, )( , )
( -3, ),函数值 的
大小关系是( )D1、已知反比例函数,其图象所在的每个象限内随着的增大而增大,请写出一个符合条件的反比例函数关系式:复练2、 已知点(-1, ),(2, ),(3, )在反比例函数 的图象上. 下列结论中正确的是( )B复练3、反比例函数的关系式D例5:( 天津)已知图中的曲线是反比例函数 (m为常数)图象的一支.
(Ⅰ) 这个反比例函数图象的另一支在第几象限?常数m的取值范围是什么?
(Ⅱ)若该函数的图象与正比例函数 的图象在第一象内限的交点为A,过A点作轴的垂线,垂足为B,当 的面积为4时,求点A的坐标及反比例函数的解析式.解:(Ⅰ)这个反比例函数图象的另一支在第三象限.
因为这个反比例函数的图象分布在第一、第三象限,
所以m-5>0,解得m>5. (Ⅱ)如图,由第一象限内的点A在正比例函数y=2x的图象上,
设点A的坐标为(a,2a) (a>0),
则点B的坐标为(a,0),
解得a=2(负值舍去).
A点的坐标为(2,4).
又点A在反比例函数 的图象上, ,即:m-5=8
所以反比例函数的解析式为 .1、( 江苏淮安)若一次函数y=2x+l的图象与反比例函数图象的一个交点横坐标为l,则反比例函数关系式为 .复练2、( 山西)如图,A是反比例函数图象上一点,过点A作轴于点B,点P在x轴上,△ABP面积为2,则这个反比例函数的解析式为 。复练复练3.( 安徽省中中考) 点P(1,a)在反比例函数 的图象上,它关于轴的对称点在一次函数 y=2x+4 的图象上,求此反比例函数的解析式。例6:( 安徽)一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,如图所示,设小矩形的长和宽分别为x、y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )4、反比例函数的实际应用A1.( 重庆綦江县)有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 (单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=2m3时,气体的密度是_______kg/m3.复练4复练2.( 浙江嘉兴)一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系: ,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).
(1)求k和m的值;
(2)若行驶速度不得超过
60(km/h),则汽车通过
该路段最少需要多少时间?解:(1)将A(40,1)代入 ,解得 k=40 .
函数解析式为:
当t=0.5时,解得m=80
所以,k=40 , m=80 .
(2)令v=60,得.
结合函数图象可知,汽车通过该路段最少需要 小时. 5、反比例函数的综合运用例7.( 北京)已知反比例函数 的图像经过点A( ,1)
(1)试确定此反比例函数的解析式.
(2)点O是坐标原点,将线段OA绕点O顺时针旋转30°得到线段OB,判断点B是否在反比例函数的图像上,并说明理由.
(3)已知点P(m, )也在此反比例函数的图像上(其中m <0),过p点作x轴的的垂线,交x轴于点M,若线段PM上存在一点Q,使得△OQM的面积是 ,设Q点的纵坐标为n,求 的值.1、( 温州)如图,在平面直角坐标系中,直线AB与Y轴和X轴分别交于点A、点B,与反比例函数 在第一象限的图象交于点c(1,6)、点D(3,y).过点C作CE上y轴于E,过点D作DF上X轴于F.
(1)求m,n的值;
(2)求直线AB的函数解析式;
(3)求证:△AEC∽△DFB.复练2、( 兰州)如图,已知,
A(-4,n),B(2,-4)是一次函数 的图象和反比例函数 的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与X轴的交点C的坐标及△AOB的面积;
(3)求 方程的解(请直接写出答案);
(4)求 不等式的解集(请直接写出答案).复练y=-x-2
