17.3 分式方程[下学期]
图片预览







文档简介
课件25张PPT。课 时 计 划
第 周 星期六 第1、2、3、4节 2005年7月23日
课题:21.4.1
教学目标:
了解解分式方程的一般步骤。
教材分析:
重点:体会解分式方程的方法,并了解增根的产生,注意要验根。
难点:解分式方程的方法中,每一项必须同时乘以最简公分母,并验根。
教具:多媒体
教学方法:讨论、练习、总结式教学
教学过程:可化为一元一次方程的分式方程复习:
问题1、什么叫方程?什么叫做方程的解(根)?
问题2:什么叫做一元一次方程?
问题3:解方程的步骤是怎样的?情景1:某地电话公司调低了长途电话的话费标准,每分费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分时间,问前后两种收费标准每分收费各是多少?在上面的问题中,主要等量关系是什么?6元话费 按原收费标准的通话时间+5
= 按新收费标准的通话时间= +5情景2:轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同。已知水流的速度是3千米/时,求轮船在静水中的速度。在上面的问题中,主要等量关系是什么?顺水中航行80千米所需的时间
=逆水航行60千米所需的时间如果设轮船在静水中的速度为x千米/时,则得方程:= 只含分式,或分式和整式,并且 的方程叫做分式方程.练习2:下列方程中,哪些是分式方程,哪些不是分式方程?为什么?分母里含有未知数如何求解分式方程?含有未知数的分母应如何处理?问题5:想一想,我们应如何解分式方程?由此可知:
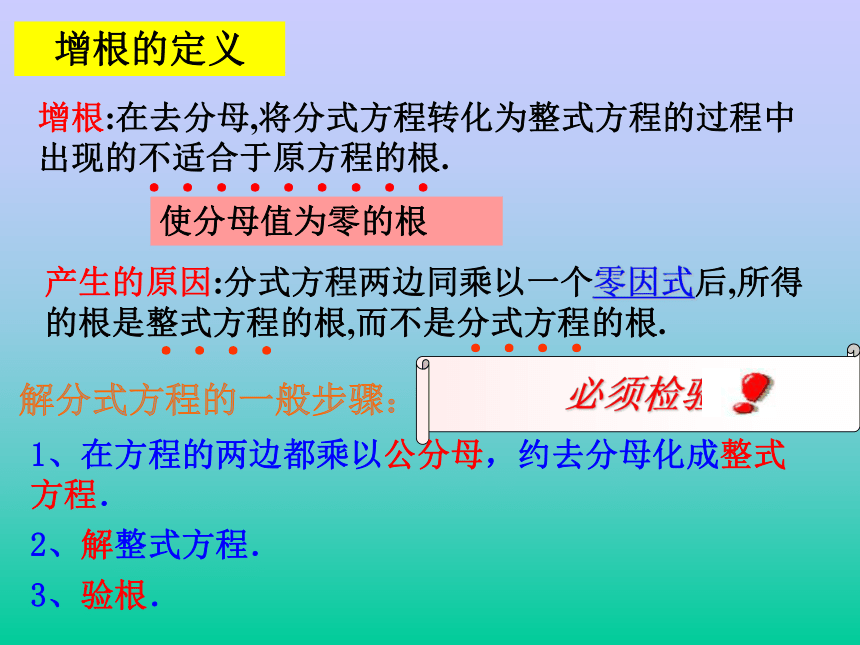
分式方程的解法是类似于一元一次方程的解法的。当x=-1时,使得分式方程的左右两边没有意义。产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.········使分母值为零的根·········解分式方程的一般步骤:1、在方程的两边都乘以公分母,约去分母化成整式方程.
2、解整式方程.
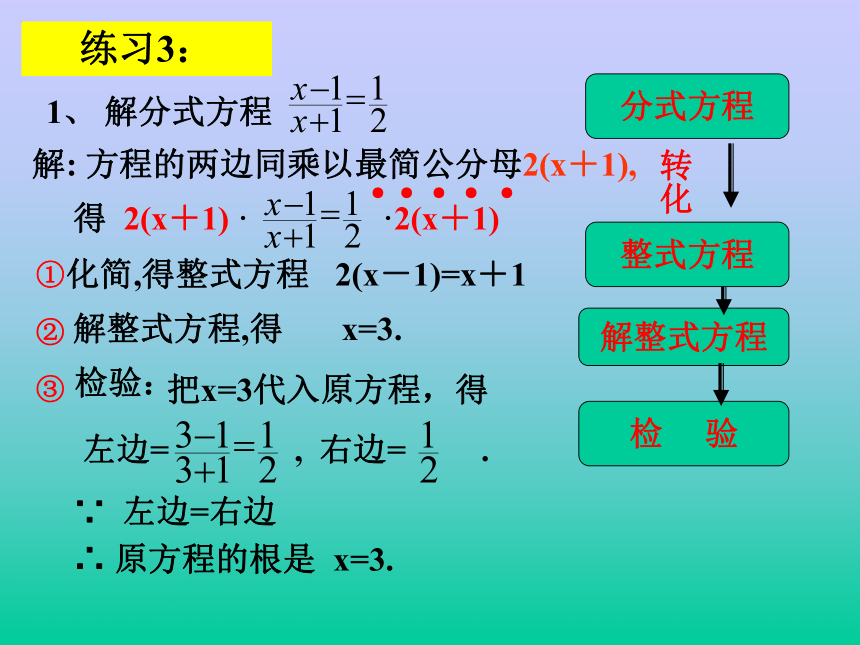
3、验根.1、 解分式方程 化简,得整式方程 2(x-1)=x+1解整式方程,得 x=3. 把x=3代入原方程,得
左边= , 右边= .∵ 左边=右边∴ 原方程的根是 x=3.● ● ● ● ●分式方程整式方程解整式方程检 验转化① ② ③检验:练习3:得 2(x+1) · ·2(x+1)检验可有新方法?使分母为零的未知数的值,就是增根.试说明这样检验的理由.归纳:解分式方程的一般步骤1、在方程的两边都乘以公分母,约去分母化成整式方程.
2、解整式方程.
3、验根.(可代入原方程,或代入公分母。)Cx=2x-1-127、当m为何值时,去分母解方程:
会产生增根?反思:分式方程产生增根,也就是使分母等于0.
将原分式方程去分母后,代入增根.没有解.改错解分式方程:解:方程两边都乘以 ,得解这个整式方程,得检验:当 时,∴ 是原方程的根。总结:3、解分式方程一般需要哪几个步骤?
①去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
②解整式方程.
③检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
④结论 :确定分式方程的解.这里的检验要以计算正确为前提4、解分式方程容易犯的错误主要有:(1)去分母时,原方程整式部分漏乘即每一项都需乘以最简公分母。
(2)约去分母后,分子是多项式时, 要注意添括号.
(3)增根不舍掉.
(4)要注意灵活运用解分式方程的步骤。同时要有简算意识,提高运算的速度和准确性。体会数学转化的思想方法.…… 中考链接:1.(连云港)若关于x的方程 无解,则m的值是_________;
2.(上海)在方程 中,如果y=x2-3x,那么原方程可化为关于x的整式方程是_________;
3.(南通)解分式方程-1或0或3A7、解方程组:布置作业:
作业练习卷(分式方程)
板书设计:
课题
1、分式方程的定义
2、分式方程的解法 投影幕
3、解分式方程的步骤
学生板演
第 周 星期六 第1、2、3、4节 2005年7月23日
课题:21.4.1
教学目标:
了解解分式方程的一般步骤。
教材分析:
重点:体会解分式方程的方法,并了解增根的产生,注意要验根。
难点:解分式方程的方法中,每一项必须同时乘以最简公分母,并验根。
教具:多媒体
教学方法:讨论、练习、总结式教学
教学过程:可化为一元一次方程的分式方程复习:
问题1、什么叫方程?什么叫做方程的解(根)?
问题2:什么叫做一元一次方程?
问题3:解方程的步骤是怎样的?情景1:某地电话公司调低了长途电话的话费标准,每分费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分时间,问前后两种收费标准每分收费各是多少?在上面的问题中,主要等量关系是什么?6元话费 按原收费标准的通话时间+5
= 按新收费标准的通话时间= +5情景2:轮船在顺水中航行80千米所需的时间和逆水航行60千米所需的时间相同。已知水流的速度是3千米/时,求轮船在静水中的速度。在上面的问题中,主要等量关系是什么?顺水中航行80千米所需的时间
=逆水航行60千米所需的时间如果设轮船在静水中的速度为x千米/时,则得方程:= 只含分式,或分式和整式,并且 的方程叫做分式方程.练习2:下列方程中,哪些是分式方程,哪些不是分式方程?为什么?分母里含有未知数如何求解分式方程?含有未知数的分母应如何处理?问题5:想一想,我们应如何解分式方程?由此可知:
分式方程的解法是类似于一元一次方程的解法的。当x=-1时,使得分式方程的左右两边没有意义。产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.增根的定义增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.········使分母值为零的根·········解分式方程的一般步骤:1、在方程的两边都乘以公分母,约去分母化成整式方程.
2、解整式方程.
3、验根.1、 解分式方程 化简,得整式方程 2(x-1)=x+1解整式方程,得 x=3. 把x=3代入原方程,得
左边= , 右边= .∵ 左边=右边∴ 原方程的根是 x=3.● ● ● ● ●分式方程整式方程解整式方程检 验转化① ② ③检验:练习3:得 2(x+1) · ·2(x+1)检验可有新方法?使分母为零的未知数的值,就是增根.试说明这样检验的理由.归纳:解分式方程的一般步骤1、在方程的两边都乘以公分母,约去分母化成整式方程.
2、解整式方程.
3、验根.(可代入原方程,或代入公分母。)Cx=2x-1-127、当m为何值时,去分母解方程:
会产生增根?反思:分式方程产生增根,也就是使分母等于0.
将原分式方程去分母后,代入增根.没有解.改错解分式方程:解:方程两边都乘以 ,得解这个整式方程,得检验:当 时,∴ 是原方程的根。总结:3、解分式方程一般需要哪几个步骤?
①去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
②解整式方程.
③检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
④结论 :确定分式方程的解.这里的检验要以计算正确为前提4、解分式方程容易犯的错误主要有:(1)去分母时,原方程整式部分漏乘即每一项都需乘以最简公分母。
(2)约去分母后,分子是多项式时, 要注意添括号.
(3)增根不舍掉.
(4)要注意灵活运用解分式方程的步骤。同时要有简算意识,提高运算的速度和准确性。体会数学转化的思想方法.…… 中考链接:1.(连云港)若关于x的方程 无解,则m的值是_________;
2.(上海)在方程 中,如果y=x2-3x,那么原方程可化为关于x的整式方程是_________;
3.(南通)解分式方程-1或0或3A7、解方程组:布置作业:
作业练习卷(分式方程)
板书设计:
课题
1、分式方程的定义
2、分式方程的解法 投影幕
3、解分式方程的步骤
学生板演
