人教版八年级下册 18.2.2 菱形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册 18.2.2 菱形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 505.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 17:49:07 | ||
图片预览


文档简介
18.2.2 菱形 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题是真命题的是( )
A.对角线互相垂直且相等的四边形是菱形
B.对角线互相平分且相等的四边形是菱形
C.对角线互相平分且垂直的四边形是菱形
D.对角线互相垂直的四边形是菱形
2.如图,菱形的对角线、相交于点O,若,,则菱形的边长为( )
A. B. C.8 D.10
3.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
4.如图,菱形的边长为2,,则点A的坐标为( )
A. B. C. D.
5.如图,菱形ABCD中,AC交BD于点O,于点E,连接OE,若,则( )
A.20° B.30° C.40° D.50°
6.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
7.在菱形ABCD中,对角线AC、BD相交于点O,AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为( )
A.22 B.24 C.48 D.44
8.如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )
A.AF=CF B.∠FAC=∠EAC C.AB=4 D.AC=2AB
9.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
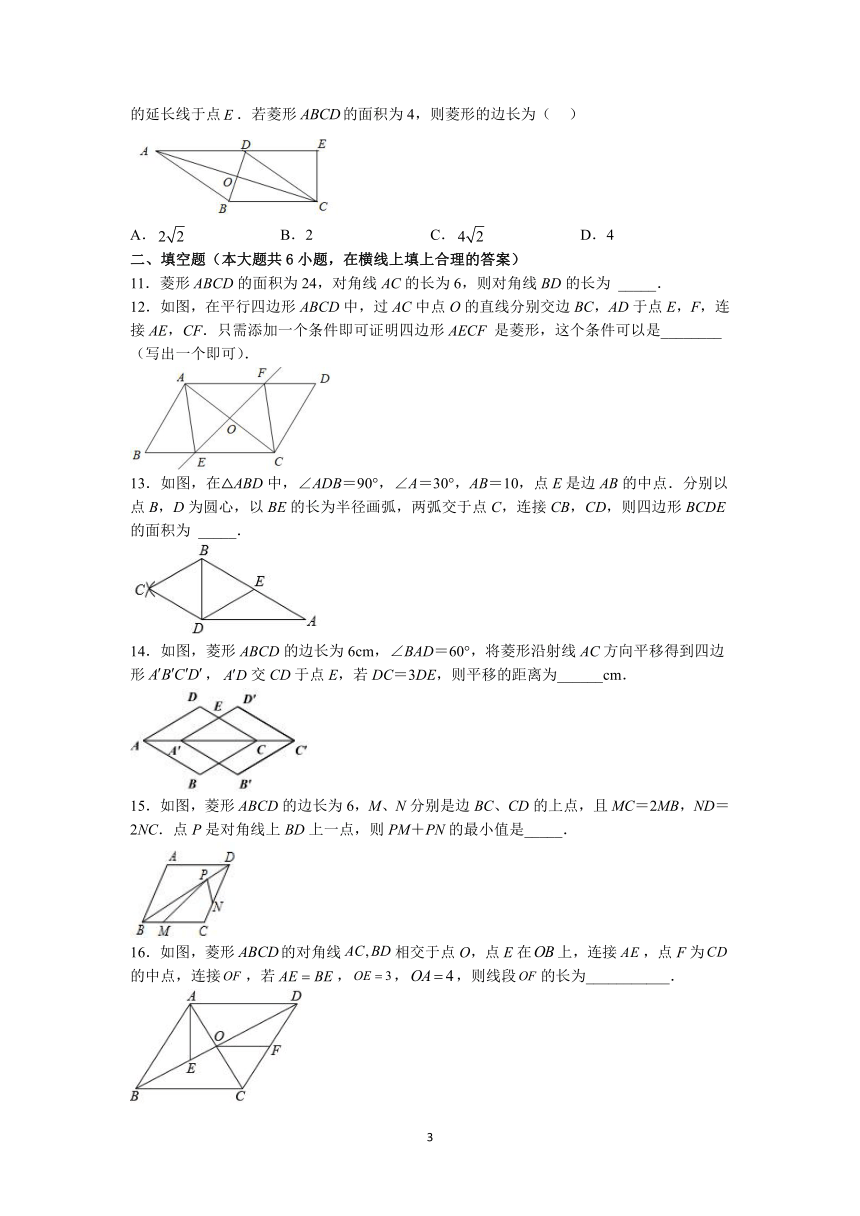
10.如图,菱形对角线,交于点,,过点作交的延长线于点.若菱形的面积为4,则菱形的边长为( )
A. B.2 C. D.4
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.菱形ABCD的面积为24,对角线AC的长为6,则对角线BD的长为 _____.
12.如图,在平行四边形ABCD中,过AC中点O的直线分别交边BC,AD于点E,F,连接AE,CF.只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是________(写出一个即可).
13.如图,在△ABD中,∠ADB=90°,∠A=30°,AB=10,点E是边AB的中点.分别以点B,D为圆心,以BE的长为半径画弧,两弧交于点C,连接CB,CD,则四边形BCDE的面积为 _____.
14.如图,菱形ABCD的边长为6cm,∠BAD=60°,将菱形沿射线AC方向平移得到四边形,交CD于点E,若DC=3DE,则平移的距离为______cm.
15.如图,菱形ABCD的边长为6,M、N分别是边BC、CD的上点,且MC=2MB,ND=2NC.点P是对角线上BD上一点,则PM+PN的最小值是_____.
16.如图,菱形的对角线相交于点O,点E在上,连接,点F为的中点,连接,若,,,则线段的长为___________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
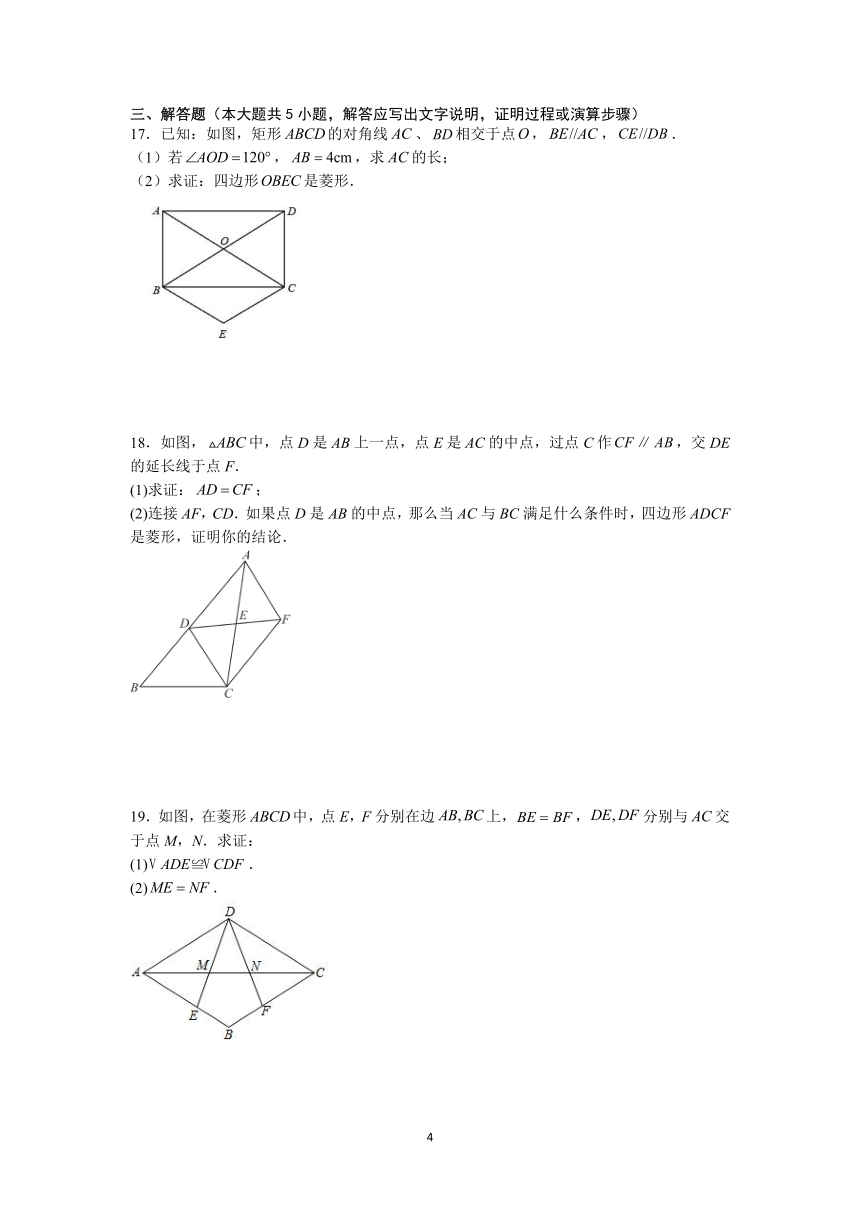
17.已知:如图,矩形的对角线、相交于点,,.
(1)若,,求的长;
(2)求证:四边形是菱形.
18.如图,中,点D是AB上一点,点E是AC的中点,过点C作,交DE的延长线于点F.
(1)求证:;
(2)连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形,证明你的结论.
19.如图,在菱形中,点E,F分别在边上,,分别与交于点M,N.求证:
(1).
(2).
20.如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积.
21.如图,四边形是矩形,E、F分别是线段、上的点,点O是与的交点.若将沿直线折叠,则点E与点F重合.
(1)求证:四边形是菱形;
(2)若,求的值.
答案:
1.C 2.A 3.B 4.D 5.A 6.C 7.B 8.D 9.D 10.A 11.8
12.(答案不唯一) 13. 14. 15.6 16.
17.解:(1)四边形是矩形,
,
,
,
是等边三角形,
,
;
(2),,
四边形是平行四边形,
,
平行四边形是菱形.
18.(1)证明:∵,
∴∠ADF=∠CFD,∠DAC=∠FCA.
∵点E是AC的中点,
∴AE=CE,
∴,
∴;
(2)解:当时,四边形ADCF是菱形.
证明如下:
由(1)知,,
∵,
∴四边形ADCF是平行四边形.
∵,
∴是直角三角形.
∵点D是AB的中点,
∴,
∴四边形ADCF是菱形.
19.(1)证明:由菱形的性质可知,,,
∵ ,
∴,即,
在和中,
,
∴.
(2)证明:如图,连接BD交AC于点O,
由菱形的性质可知,,
∴,
由(1)知,
∴,,
∴,
∴,
在和中,
,
∴.
∴,
∴,
∴.
20.(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD,
∴AB=AD,
∴四边形ABCD是菱形;
(2)连接BD交AC于O,
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OC=AC=×6=3,
∵AB=5,AO=3,
∴BO===4,
∴BD=2BO=8,
∴S平行四边形ABCD=×AC×BD=24.
21.解:(1)证明:∵△BED沿直线BE折叠,点E与点F重合,
∴BE=BF,DE=DF,∠EDB=∠FDB,
又∵四边形ABCD是矩形,且E、F分别是线段AD、BC上的点,
∴DE∥DF,
∴∠EDB=∠FBD,
∴∠FDB=∠FBD,
∴BF=DF,
∴BE=BF=DF=DE,
∴四边形BEDF是菱形;
(2)∵ED=2AE,点E是线段AD上的点,
∴ED=AD,
∵四边形BEDF是菱形,四边形ABCD是矩形,
∴S菱形BEDF=EF·BD=ED·AB=AD·AB,
∵AB·AD=,
∴EF·BD=,
解得:EF·BD=.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题是真命题的是( )
A.对角线互相垂直且相等的四边形是菱形
B.对角线互相平分且相等的四边形是菱形
C.对角线互相平分且垂直的四边形是菱形
D.对角线互相垂直的四边形是菱形
2.如图,菱形的对角线、相交于点O,若,,则菱形的边长为( )
A. B. C.8 D.10
3.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
4.如图,菱形的边长为2,,则点A的坐标为( )
A. B. C. D.
5.如图,菱形ABCD中,AC交BD于点O,于点E,连接OE,若,则( )
A.20° B.30° C.40° D.50°
6.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A.6 B.12 C.24 D.48
7.在菱形ABCD中,对角线AC、BD相交于点O,AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为( )
A.22 B.24 C.48 D.44
8.如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )
A.AF=CF B.∠FAC=∠EAC C.AB=4 D.AC=2AB
9.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
10.如图,菱形对角线,交于点,,过点作交的延长线于点.若菱形的面积为4,则菱形的边长为( )
A. B.2 C. D.4
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.菱形ABCD的面积为24,对角线AC的长为6,则对角线BD的长为 _____.
12.如图,在平行四边形ABCD中,过AC中点O的直线分别交边BC,AD于点E,F,连接AE,CF.只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是________(写出一个即可).
13.如图,在△ABD中,∠ADB=90°,∠A=30°,AB=10,点E是边AB的中点.分别以点B,D为圆心,以BE的长为半径画弧,两弧交于点C,连接CB,CD,则四边形BCDE的面积为 _____.
14.如图,菱形ABCD的边长为6cm,∠BAD=60°,将菱形沿射线AC方向平移得到四边形,交CD于点E,若DC=3DE,则平移的距离为______cm.
15.如图,菱形ABCD的边长为6,M、N分别是边BC、CD的上点,且MC=2MB,ND=2NC.点P是对角线上BD上一点,则PM+PN的最小值是_____.
16.如图,菱形的对角线相交于点O,点E在上,连接,点F为的中点,连接,若,,,则线段的长为___________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.已知:如图,矩形的对角线、相交于点,,.
(1)若,,求的长;
(2)求证:四边形是菱形.
18.如图,中,点D是AB上一点,点E是AC的中点,过点C作,交DE的延长线于点F.
(1)求证:;
(2)连接AF,CD.如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形,证明你的结论.
19.如图,在菱形中,点E,F分别在边上,,分别与交于点M,N.求证:
(1).
(2).
20.如图,在 ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF
(1)求证: ABCD是菱形;
(2)若AB=5,AC=6,求 ABCD的面积.
21.如图,四边形是矩形,E、F分别是线段、上的点,点O是与的交点.若将沿直线折叠,则点E与点F重合.
(1)求证:四边形是菱形;
(2)若,求的值.
答案:
1.C 2.A 3.B 4.D 5.A 6.C 7.B 8.D 9.D 10.A 11.8
12.(答案不唯一) 13. 14. 15.6 16.
17.解:(1)四边形是矩形,
,
,
,
是等边三角形,
,
;
(2),,
四边形是平行四边形,
,
平行四边形是菱形.
18.(1)证明:∵,
∴∠ADF=∠CFD,∠DAC=∠FCA.
∵点E是AC的中点,
∴AE=CE,
∴,
∴;
(2)解:当时,四边形ADCF是菱形.
证明如下:
由(1)知,,
∵,
∴四边形ADCF是平行四边形.
∵,
∴是直角三角形.
∵点D是AB的中点,
∴,
∴四边形ADCF是菱形.
19.(1)证明:由菱形的性质可知,,,
∵ ,
∴,即,
在和中,
,
∴.
(2)证明:如图,连接BD交AC于点O,
由菱形的性质可知,,
∴,
由(1)知,
∴,,
∴,
∴,
在和中,
,
∴.
∴,
∴,
∴.
20.(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
∵BE=DF,
∴△AEB≌△AFD,
∴AB=AD,
∴四边形ABCD是菱形;
(2)连接BD交AC于O,
∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,
AO=OC=AC=×6=3,
∵AB=5,AO=3,
∴BO===4,
∴BD=2BO=8,
∴S平行四边形ABCD=×AC×BD=24.
21.解:(1)证明:∵△BED沿直线BE折叠,点E与点F重合,
∴BE=BF,DE=DF,∠EDB=∠FDB,
又∵四边形ABCD是矩形,且E、F分别是线段AD、BC上的点,
∴DE∥DF,
∴∠EDB=∠FBD,
∴∠FDB=∠FBD,
∴BF=DF,
∴BE=BF=DF=DE,
∴四边形BEDF是菱形;
(2)∵ED=2AE,点E是线段AD上的点,
∴ED=AD,
∵四边形BEDF是菱形,四边形ABCD是矩形,
∴S菱形BEDF=EF·BD=ED·AB=AD·AB,
∵AB·AD=,
∴EF·BD=,
解得:EF·BD=.
