第2课6.2.1方程的简单变形[下学期]
文档属性
| 名称 | 第2课6.2.1方程的简单变形[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 839.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-02 08:08:00 | ||
图片预览



文档简介
课件14张PPT。课前小测P19 3、4、7
要求:1、写好题号,不用抄题
2、解:设未知数
3、列出方程
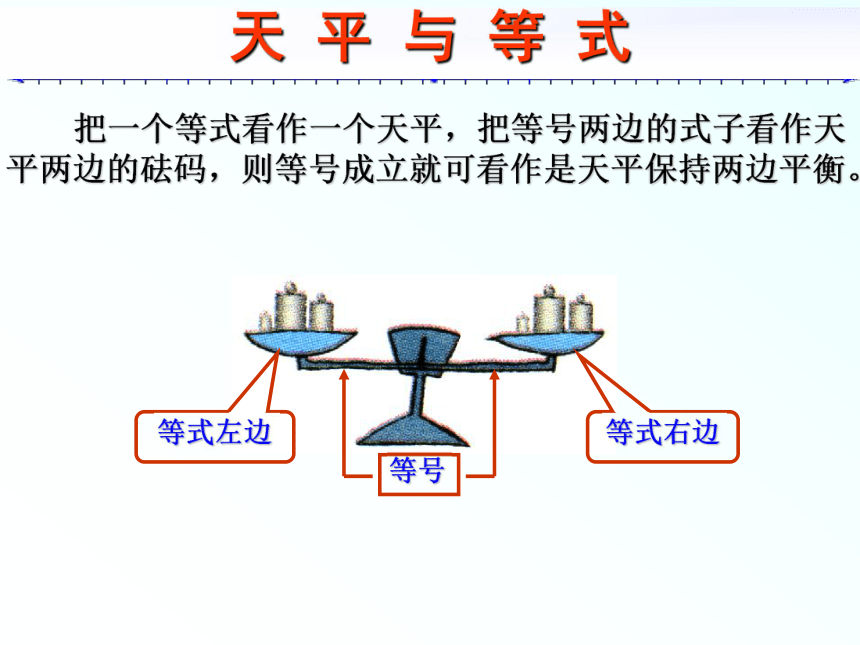
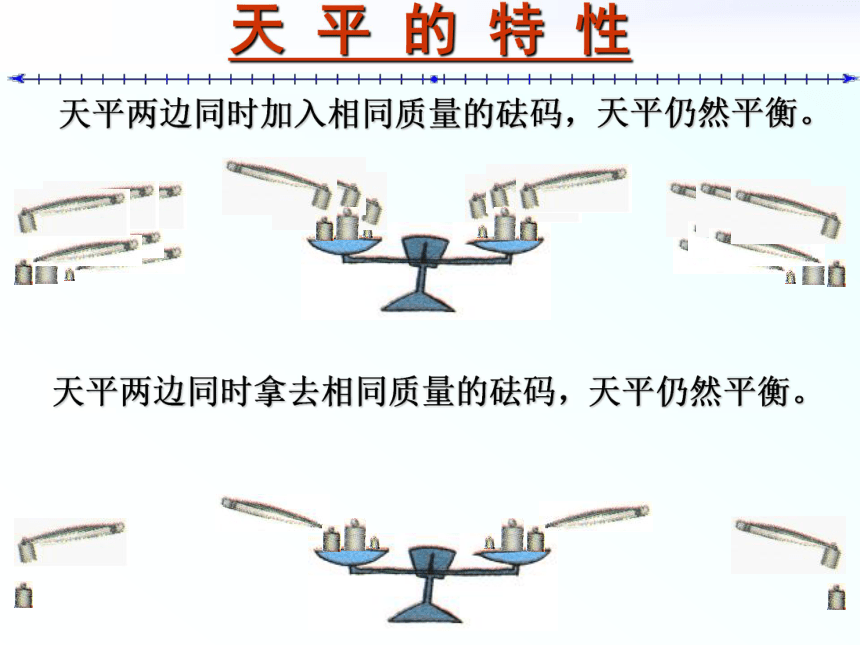
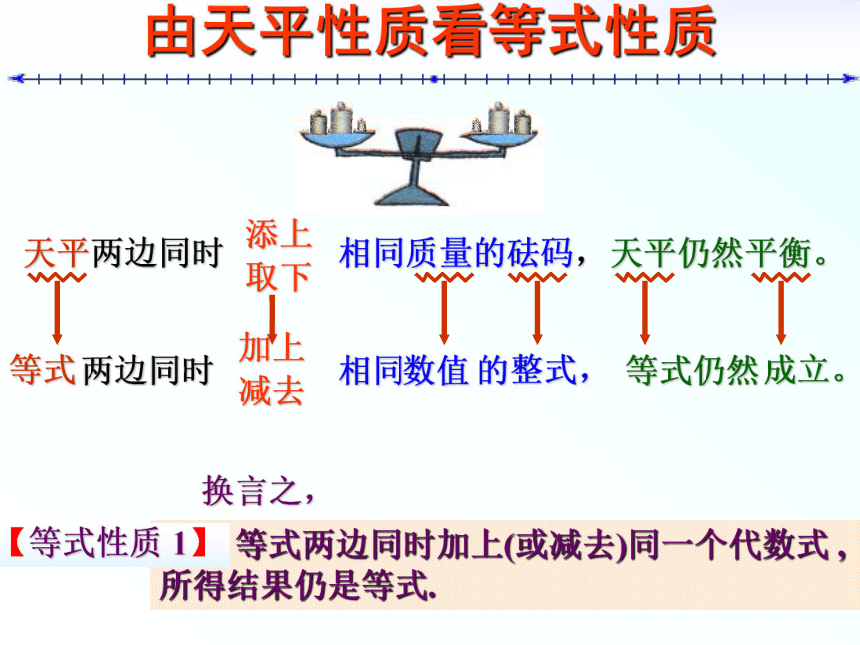
4、留空4行,再写下一题 1.方程的简单变形第六章 解一元一次方程《数学》(华师大.七年级 下册)天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡。天 平 的 特 性天平两边同时加入相同质量的砝码,天平仍然平衡。天平仍然平衡。由天平性质看等式性质天平两边同时天平仍然平衡。添上取下相同质量的砝码,等式加上减去数值整式,等式成立。换言之, 等式两边同时加上(或减去)同一个代数式 ,
所得结果仍是等式.【等式性质 1】等 式 的 性 质 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一),那么天平还保持两边平衡吗? 于是 , 你又能得出等式的什么性质?
试用准确、简明的语言叙述之. 等式两边同时乘以同一个数 (或除以同一个非零的数) , 【等式性质 2】所得结果仍是等式.代数式数代数式包括了数,且可能含有字母。用等式的性质解方程 例1 解下列方程:
(1) x -5 = 7 ; (2) x + 6 =2 ;
归 纳 像这样,将方程两边都加上(或减去)
同一个数或同一个整式,就相当于把方程中的某些项改变符号后,从方程的一边移到另一边,这样的变形叫做移项。
注意:移项时要变号。利用移项解方程:
(3) 4x = 3x-4; (4) 3 y-1= 2y-5 .
用等式的性质解方程 例2 解下列方程:
(1) -5x = 2 ; (2) P6 练习: 1、2、3解 题 后 的 反 思(1) 怎样才叫做“方程解完了”?(2) 对方程的两种变形目的是什么? x + b = c ? x = c-b最终把方程化为最简的形式:x = c
移项系数化为1例3 解下列方程 (1) 8x=2x-7 ; (2) 6=8+2x解:
(1)移项得 8x-2x=-7
即 6x=-7
两边同时除以6得 x=-7/6
(2)移项得 6-8=2x
即 -2=2x
两边同时除以2得 -1=x
即 x=-1
如何移项解这个方程?例4 解下列方程 你还有更好的解法吗?想一想:应如何选择解方程的步骤? P7 习题 6.2.1的第1题.
P19 第2题(1)
新课标 P3~4
作业 方程知识的应用 例4 方程 2x+1=3和方程2x-a=0
的解相同,求a的值.
变式:关于x的方程 2x-k+5=0的解
为-1,求代数式k2-3k-4的值.
例3 小明编了这样一道题:我是4月
出生的,我的年龄的2倍加上8,正好是
我出生那一月的总天数。你猜我有几岁?
要求:1、写好题号,不用抄题
2、解:设未知数
3、列出方程
4、留空4行,再写下一题 1.方程的简单变形第六章 解一元一次方程《数学》(华师大.七年级 下册)天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡。天 平 的 特 性天平两边同时加入相同质量的砝码,天平仍然平衡。天平仍然平衡。由天平性质看等式性质天平两边同时天平仍然平衡。添上取下相同质量的砝码,等式加上减去数值整式,等式成立。换言之, 等式两边同时加上(或减去)同一个代数式 ,
所得结果仍是等式.【等式性质 1】等 式 的 性 质 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一),那么天平还保持两边平衡吗? 于是 , 你又能得出等式的什么性质?
试用准确、简明的语言叙述之. 等式两边同时乘以同一个数 (或除以同一个非零的数) , 【等式性质 2】所得结果仍是等式.代数式数代数式包括了数,且可能含有字母。用等式的性质解方程 例1 解下列方程:
(1) x -5 = 7 ; (2) x + 6 =2 ;
归 纳 像这样,将方程两边都加上(或减去)
同一个数或同一个整式,就相当于把方程中的某些项改变符号后,从方程的一边移到另一边,这样的变形叫做移项。
注意:移项时要变号。利用移项解方程:
(3) 4x = 3x-4; (4) 3 y-1= 2y-5 .
用等式的性质解方程 例2 解下列方程:
(1) -5x = 2 ; (2) P6 练习: 1、2、3解 题 后 的 反 思(1) 怎样才叫做“方程解完了”?(2) 对方程的两种变形目的是什么? x + b = c ? x = c-b最终把方程化为最简的形式:x = c
移项系数化为1例3 解下列方程 (1) 8x=2x-7 ; (2) 6=8+2x解:
(1)移项得 8x-2x=-7
即 6x=-7
两边同时除以6得 x=-7/6
(2)移项得 6-8=2x
即 -2=2x
两边同时除以2得 -1=x
即 x=-1
如何移项解这个方程?例4 解下列方程 你还有更好的解法吗?想一想:应如何选择解方程的步骤? P7 习题 6.2.1的第1题.
P19 第2题(1)
新课标 P3~4
作业 方程知识的应用 例4 方程 2x+1=3和方程2x-a=0
的解相同,求a的值.
变式:关于x的方程 2x-k+5=0的解
为-1,求代数式k2-3k-4的值.
例3 小明编了这样一道题:我是4月
出生的,我的年龄的2倍加上8,正好是
我出生那一月的总天数。你猜我有几岁?
