人教版八年级数学下册 19.2.2 一次函数 同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册 19.2.2 一次函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 535.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 18:33:09 | ||
图片预览


文档简介
19.2.2 一次函数 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
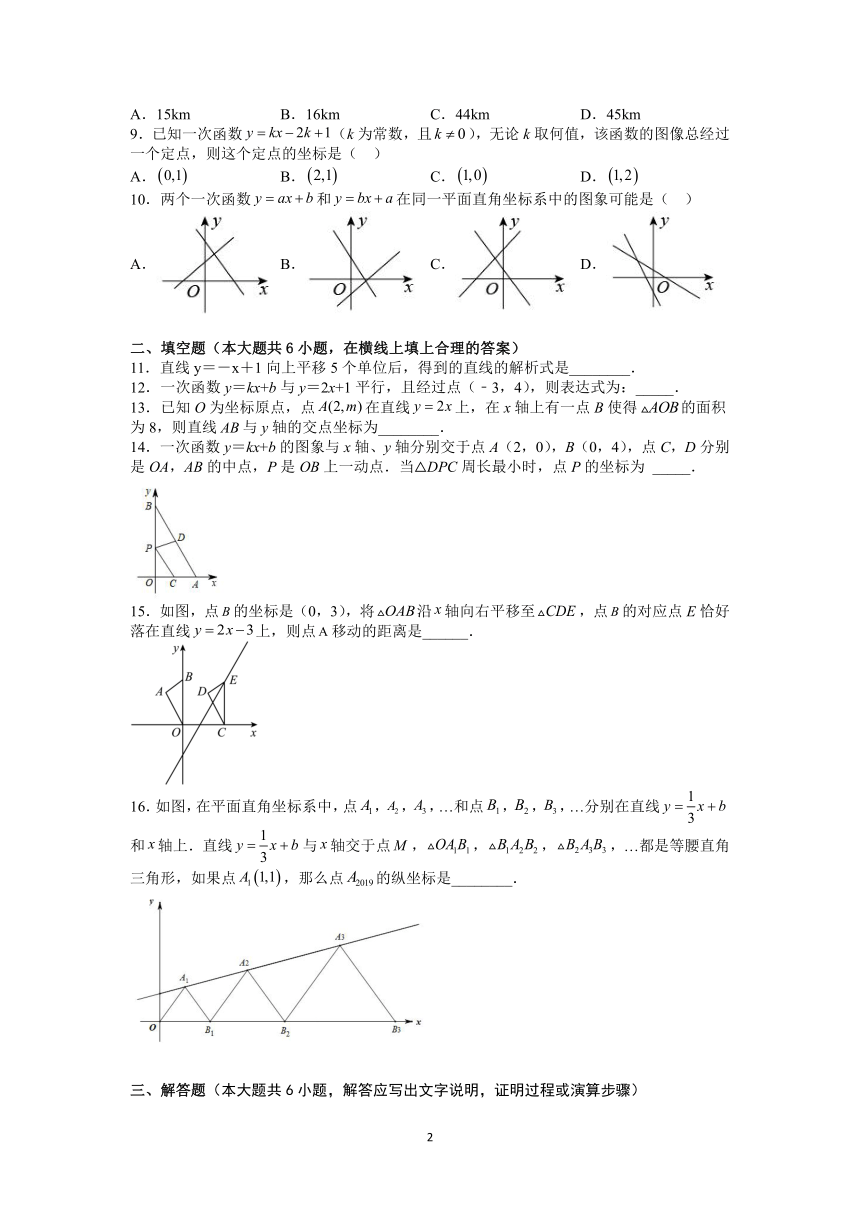
1.下列函数①;②;③;④;⑤中,是一次函数的有( ).
A.1个 B.2个 C.3个 D.4个
2.已知点,都在直线上,则,大小关系是( )
A. B. C. D.不能比较
3.下列函数图象中,表示直线的是( )
A.B.C.D.
4.关于一次函数y=﹣2x+1,下列说法不正确的是( )
A.图象与y轴的交点坐标为(0,1) B.图象与x轴的交点坐标为(,0)
C.y随x的增大而增大 D.图象不经过第三象限
5.下列一次函数中,y随x增大而增大的有( )
①;②;③;④;⑤.
A.①②③ B.①②⑤ C.①③⑤ D.①④⑤
6.一次函数与的图象如图,则下列结论:①;②;③当时,,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
7.在直角坐标系中,已知点,点是直线上的两点,则,的大小关系是( )
A. B. C. D.
8.已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15km B.16km C.44km D.45km
9.已知一次函数(k为常数,且),无论k取何值,该函数的图像总经过一个定点,则这个定点的坐标是( )
A. B. C. D.
10.两个一次函数和在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.直线y=-x+1向上平移5个单位后,得到的直线的解析式是________.
12.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
13.已知O为坐标原点,点在直线上,在x轴上有一点B使得的面积为8,则直线与y轴的交点坐标为________.
14.一次函数y=kx+b的图象与x轴、y轴分别交于点A(2,0),B(0,4),点C,D分别是OA,AB的中点,P是OB上一动点.当△DPC周长最小时,点P的坐标为 _____.
15.如图,点的坐标是(0,3),将沿轴向右平移至,点的对应点E恰好落在直线上,则点移动的距离是______.
16.如图,在平面直角坐标系中,点,,,…和点,,,…分别在直线和轴上.直线与轴交于点,,,,…都是等腰直角三角形,如果点,那么点的纵坐标是________.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.已知一次函数的图象过和两点.
(1)求此一次函数的解析式;
(2)若点在这个函数图象上,求a.
18.已知:一次函数的图象经过,两点.
(1)求一次函数的解析式,并画出此一次函数的图象;
(2)求当x取何值时,函数值.
19.如图,一次函数y=x+3的图象与x轴交于点B,与过点A(3,0)的一次函数的图象交于点C(1,m).
(1)求m的值;
(2)求一次函数图象相应的函数表达式;
(3)求的面积.
20.甲、乙两个探测气球分别从海拔和处同时出发,匀速上升.下图是甲、乙两个探测气球所在位置的海拔y(单位:m)与气球上升时间x(单位:)的函数图象.
(1)求这两个气球在上升过程中y关于x的函数解析式;
(2)当这两个气球的海拔高度相差时,求上升的时间.
21.在平面直角坐标系中,函数的图象经过点,,且与轴交于点.
(1)求该函数的解析式及点的坐标;
(2)当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.
22.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
答案:
C 2.B 3.B 4.C 5.C 6.B 7.A 8.A 9.B 10.B
11.y=-x+6 12.y=2x+10 13.或 14.(0,1) 15.3 16.
17.解:(1)设一次函数的解析式为y=kx+b,
把和代入得
,
解得.
所以此一次函数的解析式为;
(2)把代y=3x-1得3a-1=6,
所以.
18.解:(1)∵经过点,,
∴,解得:,∴
画出图像
(2)由图像可知,当时,
19.解:(1)∵点C(1,m)在一次函数y=x+3的图象上,
∴m=1+3=4;
(2)设一次函数图象相应的函数表达式为y=kx+b,
把点A(3,0),C(1,4)代入得,
解得,
∴一次函数图象相应的函数表达式y=﹣2x+6;
(3)∵一次函数y=x+3的图象与x轴交于点B,
∴B(﹣3,0),
∵A(3,0),C(1,4),
∴AB=6,
∴.
20.解:(1)设甲气球上升过程中:,
由题意得:甲的图像经过:两点,
解得:
所以甲上升过程中:
设乙气球上升过程中:
由题意得:乙的图像经过:两点,
解得:
所以乙上升过程中:
(2)由两个气球的海拔高度相差,
即
或
解得:或(不合题意,舍去)
所以当这两个气球的海拔高度相差时,上升的时间为
21.(1)解:将,代入函数解析式得,
,解得,
∴函数的解析式为:,
当时,得,
∴点A的坐标为.
(2)由题意得,
,即,
又由,得,
解得,
∴的取值范围为.
22.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得
4=﹣m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣;
故k的值为或2或﹣.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列函数①;②;③;④;⑤中,是一次函数的有( ).
A.1个 B.2个 C.3个 D.4个
2.已知点,都在直线上,则,大小关系是( )
A. B. C. D.不能比较
3.下列函数图象中,表示直线的是( )
A.B.C.D.
4.关于一次函数y=﹣2x+1,下列说法不正确的是( )
A.图象与y轴的交点坐标为(0,1) B.图象与x轴的交点坐标为(,0)
C.y随x的增大而增大 D.图象不经过第三象限
5.下列一次函数中,y随x增大而增大的有( )
①;②;③;④;⑤.
A.①②③ B.①②⑤ C.①③⑤ D.①④⑤
6.一次函数与的图象如图,则下列结论:①;②;③当时,,其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
7.在直角坐标系中,已知点,点是直线上的两点,则,的大小关系是( )
A. B. C. D.
8.已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15km B.16km C.44km D.45km
9.已知一次函数(k为常数,且),无论k取何值,该函数的图像总经过一个定点,则这个定点的坐标是( )
A. B. C. D.
10.两个一次函数和在同一平面直角坐标系中的图象可能是( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.直线y=-x+1向上平移5个单位后,得到的直线的解析式是________.
12.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
13.已知O为坐标原点,点在直线上,在x轴上有一点B使得的面积为8,则直线与y轴的交点坐标为________.
14.一次函数y=kx+b的图象与x轴、y轴分别交于点A(2,0),B(0,4),点C,D分别是OA,AB的中点,P是OB上一动点.当△DPC周长最小时,点P的坐标为 _____.
15.如图,点的坐标是(0,3),将沿轴向右平移至,点的对应点E恰好落在直线上,则点移动的距离是______.
16.如图,在平面直角坐标系中,点,,,…和点,,,…分别在直线和轴上.直线与轴交于点,,,,…都是等腰直角三角形,如果点,那么点的纵坐标是________.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.已知一次函数的图象过和两点.
(1)求此一次函数的解析式;
(2)若点在这个函数图象上,求a.
18.已知:一次函数的图象经过,两点.
(1)求一次函数的解析式,并画出此一次函数的图象;
(2)求当x取何值时,函数值.
19.如图,一次函数y=x+3的图象与x轴交于点B,与过点A(3,0)的一次函数的图象交于点C(1,m).
(1)求m的值;
(2)求一次函数图象相应的函数表达式;
(3)求的面积.
20.甲、乙两个探测气球分别从海拔和处同时出发,匀速上升.下图是甲、乙两个探测气球所在位置的海拔y(单位:m)与气球上升时间x(单位:)的函数图象.
(1)求这两个气球在上升过程中y关于x的函数解析式;
(2)当这两个气球的海拔高度相差时,求上升的时间.
21.在平面直角坐标系中,函数的图象经过点,,且与轴交于点.
(1)求该函数的解析式及点的坐标;
(2)当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.
22.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
答案:
C 2.B 3.B 4.C 5.C 6.B 7.A 8.A 9.B 10.B
11.y=-x+6 12.y=2x+10 13.或 14.(0,1) 15.3 16.
17.解:(1)设一次函数的解析式为y=kx+b,
把和代入得
,
解得.
所以此一次函数的解析式为;
(2)把代y=3x-1得3a-1=6,
所以.
18.解:(1)∵经过点,,
∴,解得:,∴
画出图像
(2)由图像可知,当时,
19.解:(1)∵点C(1,m)在一次函数y=x+3的图象上,
∴m=1+3=4;
(2)设一次函数图象相应的函数表达式为y=kx+b,
把点A(3,0),C(1,4)代入得,
解得,
∴一次函数图象相应的函数表达式y=﹣2x+6;
(3)∵一次函数y=x+3的图象与x轴交于点B,
∴B(﹣3,0),
∵A(3,0),C(1,4),
∴AB=6,
∴.
20.解:(1)设甲气球上升过程中:,
由题意得:甲的图像经过:两点,
解得:
所以甲上升过程中:
设乙气球上升过程中:
由题意得:乙的图像经过:两点,
解得:
所以乙上升过程中:
(2)由两个气球的海拔高度相差,
即
或
解得:或(不合题意,舍去)
所以当这两个气球的海拔高度相差时,上升的时间为
21.(1)解:将,代入函数解析式得,
,解得,
∴函数的解析式为:,
当时,得,
∴点A的坐标为.
(2)由题意得,
,即,
又由,得,
解得,
∴的取值范围为.
22.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得
4=﹣m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣;
故k的值为或2或﹣.
