【备考2023】浙教版科学中考“临阵磨枪”专题训练(十四):密度计、浮力秤【word,含解析】
文档属性
| 名称 | 【备考2023】浙教版科学中考“临阵磨枪”专题训练(十四):密度计、浮力秤【word,含解析】 | 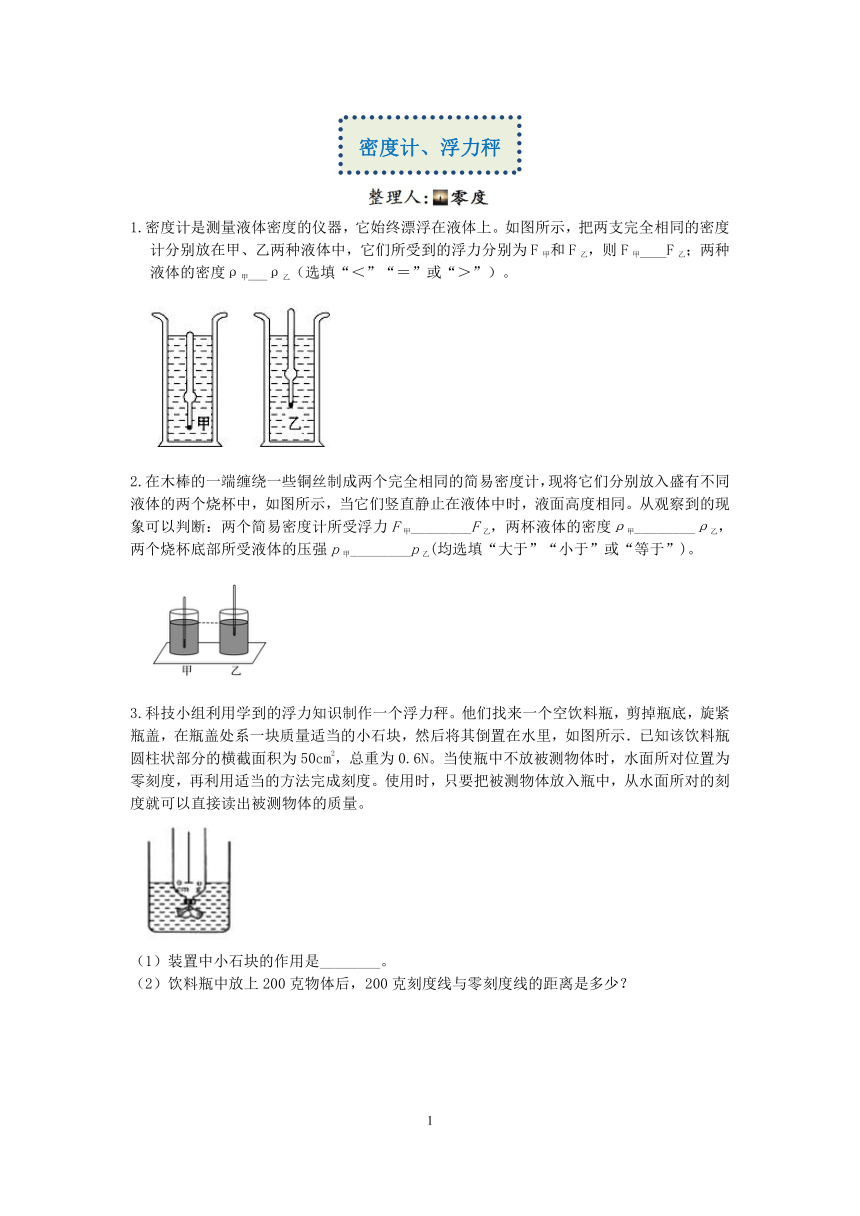 | |
| 格式 | doc | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-04-07 10:11:59 | ||
图片预览



文档简介
1.密度计是测量液体密度的仪器,它始终漂浮在液体上。如图所示,把两支完全相同的密度计分别放在甲、乙两种液体中,它们所受到的浮力分别为F甲和F乙,则F甲 F乙;两种液体的密度ρ甲 ρ乙(选填“<”“=”或“>”)。
2.在木棒的一端缠绕一些铜丝制成两个完全相同的简易密度计,现将它们分别放入盛有不同液体的两个烧杯中,如图所示,当它们竖直静止在液体中时,液面高度相同。从观察到的现象可以判断:两个简易密度计所受浮力F甲________F乙,两杯液体的密度ρ甲________ρ乙,两个烧杯底部所受液体的压强p甲________p乙(均选填“大于”“小于”或“等于”)。
3.科技小组利用学到的浮力知识制作一个浮力秤。他们找来一个空饮料瓶,剪掉瓶底,旋紧瓶盖,在瓶盖处系一块质量适当的小石块,然后将其倒置在水里,如图所示.已知该饮料瓶圆柱状部分的横截面积为50cm2,总重为0.6N。当使瓶中不放被测物体时,水面所对位置为零刻度,再利用适当的方法完成刻度。使用时,只要把被测物体放入瓶中,从水面所对的刻度就可以直接读出被测物体的质量。
(1)装置中小石块的作用是________。
(2)饮料瓶中放上200克物体后,200克刻度线与零刻度线的距离是多少?
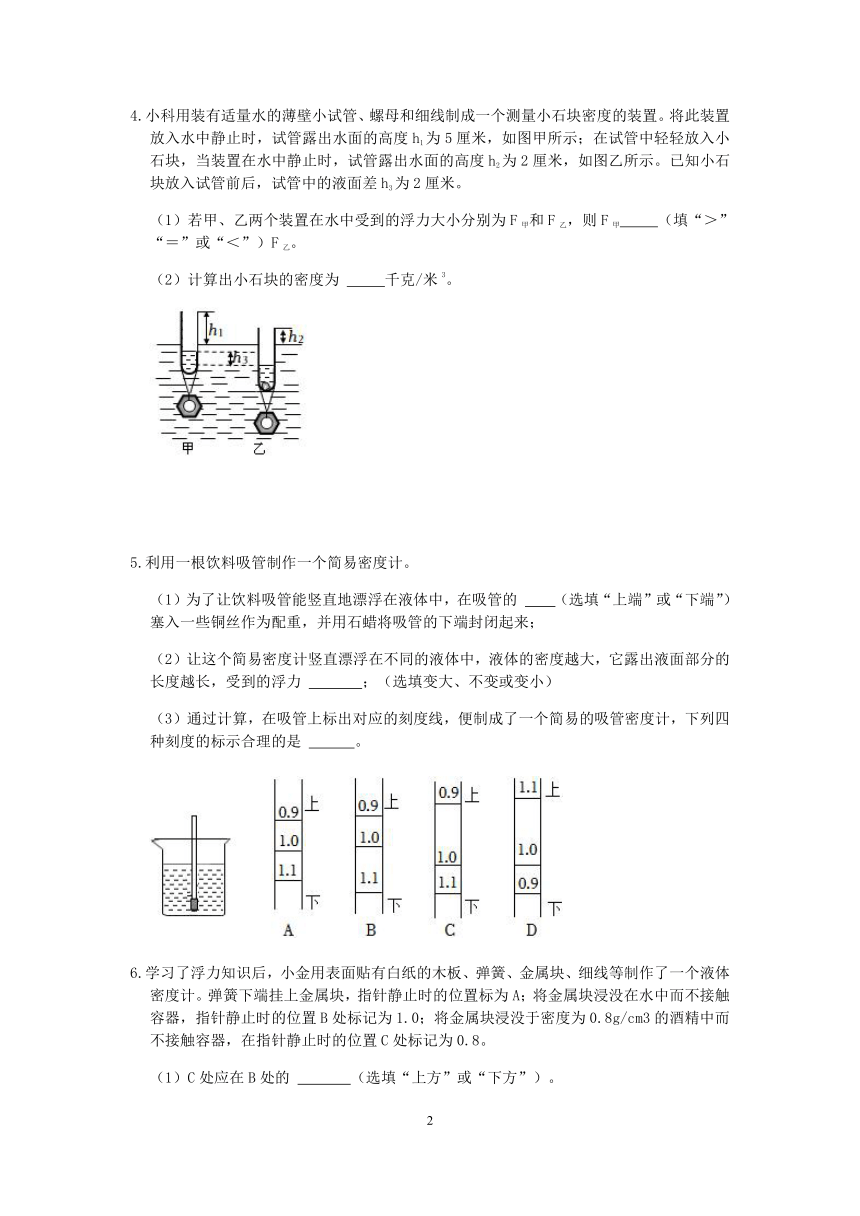
4.小科用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置。将此装置放入水中静止时,试管露出水面的高度h1为5厘米,如图甲所示;在试管中轻轻放入小石块,当装置在水中静止时,试管露出水面的高度h2为2厘米,如图乙所示。已知小石块放入试管前后,试管中的液面差h3为2厘米。
(1)若甲、乙两个装置在水中受到的浮力大小分别为F甲和F乙,则F甲 (填“>”“=”或“<”)F乙。
(2)计算出小石块的密度为 千克/米3。
5.利用一根饮料吸管制作一个简易密度计。
(1)为了让饮料吸管能竖直地漂浮在液体中,在吸管的 (选填“上端”或“下端”)塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来;
(2)让这个简易密度计竖直漂浮在不同的液体中,液体的密度越大,它露出液面部分的长度越长,受到的浮力 ;(选填变大、不变或变小)
(3)通过计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计,下列四种刻度的标示合理的是 。
6.学习了浮力知识后,小金用表面贴有白纸的木板、弹簧、金属块、细线等制作了一个液体密度计。弹簧下端挂上金属块,指针静止时的位置标为A;将金属块浸没在水中而不接触容器,指针静止时的位置B处标记为1.0;将金属块浸没于密度为0.8g/cm3的酒精中而不接触容器,在指针静止时的位置C处标记为0.8。
(1)C处应在B处的 (选填“上方”或“下方”)。
(2)B与C的中点处应标注的值 (选填“<”“>”或“=”)0.9。
(3)标记完刻度后发现刻度A与B之间的距离较小,为了增大最小刻度之间的距离,可采取的做法是 (写出一种即可)。
7.小滨同学自制简易密度计并标记刻度。他在粗细均匀的木棒底部缠绕一些细铜丝后(忽略铜丝的体积),把该密度计放入酒精中竖直漂浮,静止后露出液面的长度L1为6cm,于是他在木棒与酒精液面交界的刻度线上标记0.8g/cm3;小滨同学又把该密度计放入水中竖直漂浮,静止后露出液面的长度L2为8cm,则与水面相对应的刻度线上应标记
g/cm3。密度计上标记1.25g/cm3的刻度线到密度计顶端的距离L3为 cm。该密度计的刻度线是否均匀?并说明理由: 。
8.小金学了浮力的知识后,想制造一台浮力秤。他将一段密度为0.5×103千克/米3,粗细均匀的木料,先进行不吸水处理,再将其竖立水中,如图所示。这段木料长为40厘米,横截面积为0.1米2,其上表面可以作为秤盘(g=10牛/千克),问:
(1)质量为0的刻度线的位置在哪里?
(2)距离上表面10厘米处的刻度对应的质量为多少?
9.“曹冲称象”是家喻户晓的典故。某校兴趣小组模仿这一现象,制作了一把“浮力秤”。将直筒形的玻璃杯浸入水中,如图所示。已知玻璃杯的质量为100g,底面积为20cm2,高度为30cm。求:
(1)将杯子开口向上竖直放入水中时(注:水未进入杯内),求杯子受到的浮力。
(2)求此浮力秤的最大称量(即玻璃杯中所放物体的最大质量)。(已知ρ水=1.0×103千克/米3,g取10牛/千克)
10.小金自制密度计:在一根粗细均匀的吸管下端装入适量的小钢珠,然后用蜡封住并使底部平整。该密度计的总质量为27克,密度计总长为20厘米。小金将其放入水中,液面所在处标注为A,浸入深度为9厘米。(ρ酒精=0.8×103千克/米3)
(1)A标注处的密度为 千克/米3;
(2)密度计在酒精中静止时液面所处的位置在A的 (选填“上方”或“下方”);请画出该密度计在不同液体中所受浮力大小与浸入深度的关系图(不考虑密度计沉底,标出关键节点的数据);
(3)该密度计静止在某液体中,浸入深度为10厘米,求此液体的密度。
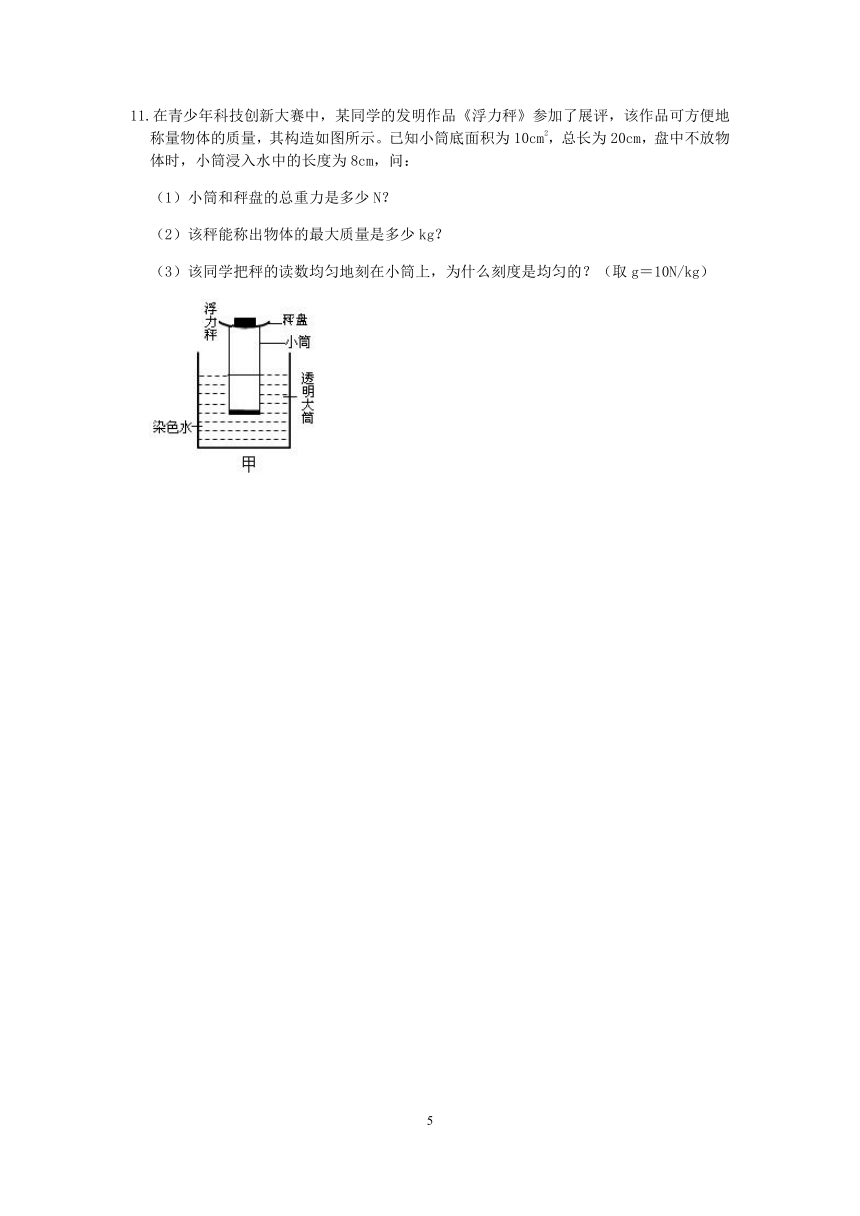
11.在青少年科技创新大赛中,某同学的发明作品《浮力秤》参加了展评,该作品可方便地称量物体的质量,其构造如图所示。已知小筒底面积为10cm2,总长为20cm,盘中不放物体时,小筒浸入水中的长度为8cm,问:
(1)小筒和秤盘的总重力是多少N?
(2)该秤能称出物体的最大质量是多少kg?
(3)该同学把秤的读数均匀地刻在小筒上,为什么刻度是均匀的?(取g=10N/kg)
答案及解析
1.解:由图可知,密度计在甲、乙液体中处于漂浮状态,
∵同一支密度计的重力不变,
∴密度计在两种液体中所受的浮力相等;故F甲=F乙;
根据阿基米德原理F浮=ρ液gV排,在F浮一定时,物体浸入液体中的体积越大,则液体的密度越小,
由题图知V排甲>V排乙,所以ρ甲<ρ乙。
故答案为:=;<。
2.等于 小于 小于
【解析】简易密度计在甲、乙两种液体中均漂浮,浮力都等于其自身重力,即相等。根据阿基米德浮力公式:F浮=G排=ρ液gV排,当浮力相同时,液体的密度与物体排开液体的体积成反比,可知乙液体的密度更大。两液面高度相同,根据公式p=ρ液gh,p甲<p乙。
3.(1)使浮力秤能竖直漂浮在水中
(2)物体处于漂浮状态,所以 ;
可得
【解析】(1)物体的重心越低越稳定,如果饮料瓶内没有小石块,那么瓶子会躺在水面上;如果放入石块,重心集中在瓶盖处,那么瓶中会竖立起来;
(2)首先根据浮沉条件计算出200g物体放入后增大的浮力,即F浮力=G物=m物g,然后再根据阿基米德原理 计算出增大的排开液体的体积,最后根据 计算两条刻度线之间的距离。
4.解:(1)将此装置放入水中静止时,排开水的体积V甲<V乙,根据F浮=ρ液gV排可知,受到的浮力F甲<F乙;
(2)比较甲、乙两图可知,两次受到的浮力之差就是小石块的重力为G=ΔF浮=ρ水g(h1﹣h2)S容=ρ水g×(0.05m﹣0.02m)S容=ρ水gS容×0.03m,
则小石块的质量mρ水S容×0.03m,
小石块放入试管前后,试管中的液面差h3为2cm,所以小石块的体积为V=(h1﹣h2﹣h3)S容=(0.05m﹣0.02m﹣0.02m)S容=0.01m×S容,
则小石块的密度ρ3ρ水=3×103kg/m3。
故答案为:<;3×103。
5.解:(1)在吸管的下端塞入一些铜丝作为配重,降低了整个吸管的重心,饮料吸管就能竖直地漂浮在液体中;
(2)密度计是漂浮在液体中,所受浮力等于本身的重力,保持不变,如果液体的密度越大,由F浮=ρ液gV排可知,密度计浸入液体中的体积越小,吸管的横截面积一定,即密度计浸入液体中的长度越短,则露出液面部分的长度越长;
(3)因为密度计是漂浮在液体中,所受浮力等于本身的重力,则F浮水=F浮液=G,即ρ水gSH=ρ液gSh=G,则hH,h和ρ液是反比例函数,所以刻度分布不均匀,且密度计的刻度由上至下数值逐渐增大,液体密度的越大时h液变化越小,故C正确;
故答案为:(1)下端;(2)不变;(3)C。
6.解:(1)根据阿基米德原理F浮=ρ液gV排可知金属块完全浸没时受到的浮力与液体密度成正比,因为0.8g/cm3<1g/cm3,所以标记为0.8时的浮力小于标记为1时的浮力。根据F=G﹣F浮可知,标记为0.8时的弹簧测力计的示数大于标记为1时的示数,因此C处应在B处的下方;
(2)当金属块完全浸没在液体中时,弹簧测力计的示数:F=G﹣F浮=G﹣ρ液gV排=﹣ρ液gV排+G,其中G、g和V排都是常量,因此测力计的示数F与液体密度ρ液为一次函数关系。即密度增大多少倍,测力计的示数也增大多少倍。因为B与C之间中点处的示数F肯定等于这两个示数和的一半,所以标注的刻度值应该为1和0.8的一半,即中点处的标注值等于0.9。
(3)刻度A和B之间的距离较小,即测力计的示数F偏小。当金属块完全浸没在液体中时,V=V排,根据公式F=G﹣ρ液gV排=ρgV﹣ρ液gV=(ρ﹣ρ液)gV可知,增大测力计示数F的方法:①增大金属块的体积;②换用更软的弹簧,相同的拉力才会伸长更大的长度。
故答案为:(1)下方;(2)=;(3)增大金属块的体积(或换用更软的弹簧,相同的拉力才会伸长更大的长度)。
7.解:设木棒长度为h,底面积为S,密度计重力为G,小滨将该密度计放入酒精中,密度计静止时L1为6cm,ρ酒精=0.8g/cm3=0.8×103kg/m3,
由F浮酒精=G,可得:ρ酒精gV排酒精=G,
即[(h﹣0.06m)S]×0.8×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣①,
小滨将该密度计放入水中,密度计静止时L2为8cm,由于水的密度ρ水=1.0g/cm3=1.0×103kg/m3,则与水面相对应的刻度线上应标记1.0g/cm3。
由F浮水=G,可得:
[(h﹣0.08m)S]×1.0×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣②,
由①②可得,h=0.16m;
设该密度计上对应密度值为1.25g/cm3的刻度线到密度计顶端的距离为L′,
则[(h﹣L′)S]×1.25×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣③,
将h=0.16m分别代入②和③,并将②③联立,
解得L=0.096m=9.6cm;
当密度计漂浮在密度为ρ液的液体中时,
因密度计始终漂浮,受到的浮力和自身的重力相等,
所以,G=F浮液,即ρgSh=ρ液gSh液,
整理可得:h液h,
由表达式可知,h液和ρ液是反比例函数,所以这种密度计的刻度是不均匀。
故答案为:1.0;9.6;不均匀,由表达式h液h可知,h液和ρ液是反比例函数。
8.(1)方法1:将这段木块竖直漂浮于水中,水面与木块相切处即为零刻度线位置
方法2:∵漂浮∴F浮=G木 又∵F浮=ρ水gV水,G木=ρ木gV木, ∴ρ水gSh=ρ木gSL,
∴h= = ,
离下表面竖直距离20cm处为零刻度线位置
(2)设距离上表面10厘米处的刻度对应的质量为m
F’浮= G水+mg
F’浮=ρ水gV’水=ρ水gSh’
=1.0×103kg/m3×10N/kg×0.1m2×(0.4-0.1)m=300N
G木=m木g=ρ木V木g=ρ木SLg
=0.5×103kg/m3×0.1m2×0.4m×10N/kg=200N
【解析】(1)根据m=ρV算出物体的质量即质量为0的刻度线的位置; (2)算出距离上表面10厘米排开水的质量减去木料的质量就是对应的质量。
9.解:
(1)杯子的重力:
G=mg=100×10﹣3kg×10N/kg=1N,
因为杯子漂浮在水面上,所以F浮=G=1N;
(2)当杯子下沉的深度为30cm=0.3m时,此时杯子受到的浮力最大,
F浮′=ρ水gV排′=1.0×103kg/m3×10N/kg×20×10﹣4m2×0.3m=6N,
最大物重G最大=F浮′﹣G=6N﹣1N=5N,
则此浮力秤的最大称量为:
m最大0.5kg。
答:(1)将杯子开口向上竖直放入水中时,杯子受到的浮力是1N。
(2)此时浮力秤的最大称量为0.5kg。
10.解:(1)根据题意知道,“小金将其放入水中,液面所在处标注为A”,所以,A处标注处的密度为水的密度,故示数应是1.0×103。
(2)该密度计的总重力:G=mg=27×10﹣3kg×10N/kg=0.27N
则图中密度计受到的浮力:F浮=G=0.27N
若将该密度计从水中取出擦干、放到密度为0.8×103kg/m3的酒精中,液体密度减小,但密度计仍然漂浮,浮力大小不变,仍然为0.27N,根据F浮=ρ液gV排知道,密度计排开液体的体积增大,露出水面的体积减小,所以,此时吸管上酒精液面的位置在A的上方。
密度计受到的浮力等于密度计的重力,不随着浸入深度的变化而变化,故该密度计在不同液体中所受浮力大小与浸入深度的关系图
(3)根据漂浮条件和据F浮=ρ液gV排知道,密度计漂浮在水中时所受浮力:F浮水=G
密度计漂浮在酒精中时所受浮力:F浮液体=G
所以F浮液体=F浮水
即ρ液体gSh液体=ρ水gSh水
故该液体的密度:0.9×103kg/m3
故答案为:(1)1.0×103;(2)上方;见上图;(3)此液体的密度0.9×103kg/m3。
11.解:(1)小筒底面积为10cm2,小筒浸入水中的长度为8cm,故小筒排开水的体积为V排=Sh=10cm2×8cm=80cm3=8×10﹣5m3
因小筒和秤盘是漂浮在水面上,故G筒=F浮=ρ液gV排=1.0×103kg/m3×10N/kg×8×10﹣5m3=0.8N;
(2)该秤测物体的最大质量时,就是V排=V筒=Sh=10cm2×20cm=200cm3=2×10﹣4m3
此时物体和小筒秤盘的总重力G=F浮=ρ液gV排=1.0×103kg/m3×10N/kg×2×10﹣4m3=2N
故此时物体的重力为G物=G﹣G筒=2N﹣0.8N=1.2N
此时物体的质量为m物0.12kg;
(3)根据以上分析可知物体质量m物;
因液体密度ρ液、小筒底面积S、小筒质量m筒都是定值,故物体质量与小筒浸入的深度是一次函数关系,故小筒上的刻度(即代表了小筒的深度)是均匀的。
答:(1)小筒和秤盘的总重力是0.8N;(2)能称出物体的最大质量是0.12kg;
(3)物体质量与小筒浸入的深度是一次函数关系,故小筒上的刻度(即代表了小筒的深度)是均匀的。
密度计、浮力秤
2.在木棒的一端缠绕一些铜丝制成两个完全相同的简易密度计,现将它们分别放入盛有不同液体的两个烧杯中,如图所示,当它们竖直静止在液体中时,液面高度相同。从观察到的现象可以判断:两个简易密度计所受浮力F甲________F乙,两杯液体的密度ρ甲________ρ乙,两个烧杯底部所受液体的压强p甲________p乙(均选填“大于”“小于”或“等于”)。
3.科技小组利用学到的浮力知识制作一个浮力秤。他们找来一个空饮料瓶,剪掉瓶底,旋紧瓶盖,在瓶盖处系一块质量适当的小石块,然后将其倒置在水里,如图所示.已知该饮料瓶圆柱状部分的横截面积为50cm2,总重为0.6N。当使瓶中不放被测物体时,水面所对位置为零刻度,再利用适当的方法完成刻度。使用时,只要把被测物体放入瓶中,从水面所对的刻度就可以直接读出被测物体的质量。
(1)装置中小石块的作用是________。
(2)饮料瓶中放上200克物体后,200克刻度线与零刻度线的距离是多少?
4.小科用装有适量水的薄壁小试管、螺母和细线制成一个测量小石块密度的装置。将此装置放入水中静止时,试管露出水面的高度h1为5厘米,如图甲所示;在试管中轻轻放入小石块,当装置在水中静止时,试管露出水面的高度h2为2厘米,如图乙所示。已知小石块放入试管前后,试管中的液面差h3为2厘米。
(1)若甲、乙两个装置在水中受到的浮力大小分别为F甲和F乙,则F甲 (填“>”“=”或“<”)F乙。
(2)计算出小石块的密度为 千克/米3。
5.利用一根饮料吸管制作一个简易密度计。
(1)为了让饮料吸管能竖直地漂浮在液体中,在吸管的 (选填“上端”或“下端”)塞入一些铜丝作为配重,并用石蜡将吸管的下端封闭起来;
(2)让这个简易密度计竖直漂浮在不同的液体中,液体的密度越大,它露出液面部分的长度越长,受到的浮力 ;(选填变大、不变或变小)
(3)通过计算,在吸管上标出对应的刻度线,便制成了一个简易的吸管密度计,下列四种刻度的标示合理的是 。
6.学习了浮力知识后,小金用表面贴有白纸的木板、弹簧、金属块、细线等制作了一个液体密度计。弹簧下端挂上金属块,指针静止时的位置标为A;将金属块浸没在水中而不接触容器,指针静止时的位置B处标记为1.0;将金属块浸没于密度为0.8g/cm3的酒精中而不接触容器,在指针静止时的位置C处标记为0.8。
(1)C处应在B处的 (选填“上方”或“下方”)。
(2)B与C的中点处应标注的值 (选填“<”“>”或“=”)0.9。
(3)标记完刻度后发现刻度A与B之间的距离较小,为了增大最小刻度之间的距离,可采取的做法是 (写出一种即可)。
7.小滨同学自制简易密度计并标记刻度。他在粗细均匀的木棒底部缠绕一些细铜丝后(忽略铜丝的体积),把该密度计放入酒精中竖直漂浮,静止后露出液面的长度L1为6cm,于是他在木棒与酒精液面交界的刻度线上标记0.8g/cm3;小滨同学又把该密度计放入水中竖直漂浮,静止后露出液面的长度L2为8cm,则与水面相对应的刻度线上应标记
g/cm3。密度计上标记1.25g/cm3的刻度线到密度计顶端的距离L3为 cm。该密度计的刻度线是否均匀?并说明理由: 。
8.小金学了浮力的知识后,想制造一台浮力秤。他将一段密度为0.5×103千克/米3,粗细均匀的木料,先进行不吸水处理,再将其竖立水中,如图所示。这段木料长为40厘米,横截面积为0.1米2,其上表面可以作为秤盘(g=10牛/千克),问:
(1)质量为0的刻度线的位置在哪里?
(2)距离上表面10厘米处的刻度对应的质量为多少?
9.“曹冲称象”是家喻户晓的典故。某校兴趣小组模仿这一现象,制作了一把“浮力秤”。将直筒形的玻璃杯浸入水中,如图所示。已知玻璃杯的质量为100g,底面积为20cm2,高度为30cm。求:
(1)将杯子开口向上竖直放入水中时(注:水未进入杯内),求杯子受到的浮力。
(2)求此浮力秤的最大称量(即玻璃杯中所放物体的最大质量)。(已知ρ水=1.0×103千克/米3,g取10牛/千克)
10.小金自制密度计:在一根粗细均匀的吸管下端装入适量的小钢珠,然后用蜡封住并使底部平整。该密度计的总质量为27克,密度计总长为20厘米。小金将其放入水中,液面所在处标注为A,浸入深度为9厘米。(ρ酒精=0.8×103千克/米3)
(1)A标注处的密度为 千克/米3;
(2)密度计在酒精中静止时液面所处的位置在A的 (选填“上方”或“下方”);请画出该密度计在不同液体中所受浮力大小与浸入深度的关系图(不考虑密度计沉底,标出关键节点的数据);
(3)该密度计静止在某液体中,浸入深度为10厘米,求此液体的密度。
11.在青少年科技创新大赛中,某同学的发明作品《浮力秤》参加了展评,该作品可方便地称量物体的质量,其构造如图所示。已知小筒底面积为10cm2,总长为20cm,盘中不放物体时,小筒浸入水中的长度为8cm,问:
(1)小筒和秤盘的总重力是多少N?
(2)该秤能称出物体的最大质量是多少kg?
(3)该同学把秤的读数均匀地刻在小筒上,为什么刻度是均匀的?(取g=10N/kg)
答案及解析
1.解:由图可知,密度计在甲、乙液体中处于漂浮状态,
∵同一支密度计的重力不变,
∴密度计在两种液体中所受的浮力相等;故F甲=F乙;
根据阿基米德原理F浮=ρ液gV排,在F浮一定时,物体浸入液体中的体积越大,则液体的密度越小,
由题图知V排甲>V排乙,所以ρ甲<ρ乙。
故答案为:=;<。
2.等于 小于 小于
【解析】简易密度计在甲、乙两种液体中均漂浮,浮力都等于其自身重力,即相等。根据阿基米德浮力公式:F浮=G排=ρ液gV排,当浮力相同时,液体的密度与物体排开液体的体积成反比,可知乙液体的密度更大。两液面高度相同,根据公式p=ρ液gh,p甲<p乙。
3.(1)使浮力秤能竖直漂浮在水中
(2)物体处于漂浮状态,所以 ;
可得
【解析】(1)物体的重心越低越稳定,如果饮料瓶内没有小石块,那么瓶子会躺在水面上;如果放入石块,重心集中在瓶盖处,那么瓶中会竖立起来;
(2)首先根据浮沉条件计算出200g物体放入后增大的浮力,即F浮力=G物=m物g,然后再根据阿基米德原理 计算出增大的排开液体的体积,最后根据 计算两条刻度线之间的距离。
4.解:(1)将此装置放入水中静止时,排开水的体积V甲<V乙,根据F浮=ρ液gV排可知,受到的浮力F甲<F乙;
(2)比较甲、乙两图可知,两次受到的浮力之差就是小石块的重力为G=ΔF浮=ρ水g(h1﹣h2)S容=ρ水g×(0.05m﹣0.02m)S容=ρ水gS容×0.03m,
则小石块的质量mρ水S容×0.03m,
小石块放入试管前后,试管中的液面差h3为2cm,所以小石块的体积为V=(h1﹣h2﹣h3)S容=(0.05m﹣0.02m﹣0.02m)S容=0.01m×S容,
则小石块的密度ρ3ρ水=3×103kg/m3。
故答案为:<;3×103。
5.解:(1)在吸管的下端塞入一些铜丝作为配重,降低了整个吸管的重心,饮料吸管就能竖直地漂浮在液体中;
(2)密度计是漂浮在液体中,所受浮力等于本身的重力,保持不变,如果液体的密度越大,由F浮=ρ液gV排可知,密度计浸入液体中的体积越小,吸管的横截面积一定,即密度计浸入液体中的长度越短,则露出液面部分的长度越长;
(3)因为密度计是漂浮在液体中,所受浮力等于本身的重力,则F浮水=F浮液=G,即ρ水gSH=ρ液gSh=G,则hH,h和ρ液是反比例函数,所以刻度分布不均匀,且密度计的刻度由上至下数值逐渐增大,液体密度的越大时h液变化越小,故C正确;
故答案为:(1)下端;(2)不变;(3)C。
6.解:(1)根据阿基米德原理F浮=ρ液gV排可知金属块完全浸没时受到的浮力与液体密度成正比,因为0.8g/cm3<1g/cm3,所以标记为0.8时的浮力小于标记为1时的浮力。根据F=G﹣F浮可知,标记为0.8时的弹簧测力计的示数大于标记为1时的示数,因此C处应在B处的下方;
(2)当金属块完全浸没在液体中时,弹簧测力计的示数:F=G﹣F浮=G﹣ρ液gV排=﹣ρ液gV排+G,其中G、g和V排都是常量,因此测力计的示数F与液体密度ρ液为一次函数关系。即密度增大多少倍,测力计的示数也增大多少倍。因为B与C之间中点处的示数F肯定等于这两个示数和的一半,所以标注的刻度值应该为1和0.8的一半,即中点处的标注值等于0.9。
(3)刻度A和B之间的距离较小,即测力计的示数F偏小。当金属块完全浸没在液体中时,V=V排,根据公式F=G﹣ρ液gV排=ρgV﹣ρ液gV=(ρ﹣ρ液)gV可知,增大测力计示数F的方法:①增大金属块的体积;②换用更软的弹簧,相同的拉力才会伸长更大的长度。
故答案为:(1)下方;(2)=;(3)增大金属块的体积(或换用更软的弹簧,相同的拉力才会伸长更大的长度)。
7.解:设木棒长度为h,底面积为S,密度计重力为G,小滨将该密度计放入酒精中,密度计静止时L1为6cm,ρ酒精=0.8g/cm3=0.8×103kg/m3,
由F浮酒精=G,可得:ρ酒精gV排酒精=G,
即[(h﹣0.06m)S]×0.8×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣①,
小滨将该密度计放入水中,密度计静止时L2为8cm,由于水的密度ρ水=1.0g/cm3=1.0×103kg/m3,则与水面相对应的刻度线上应标记1.0g/cm3。
由F浮水=G,可得:
[(h﹣0.08m)S]×1.0×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣②,
由①②可得,h=0.16m;
设该密度计上对应密度值为1.25g/cm3的刻度线到密度计顶端的距离为L′,
则[(h﹣L′)S]×1.25×103kg/m3×10N/kg=G﹣﹣﹣﹣﹣﹣﹣﹣③,
将h=0.16m分别代入②和③,并将②③联立,
解得L=0.096m=9.6cm;
当密度计漂浮在密度为ρ液的液体中时,
因密度计始终漂浮,受到的浮力和自身的重力相等,
所以,G=F浮液,即ρgSh=ρ液gSh液,
整理可得:h液h,
由表达式可知,h液和ρ液是反比例函数,所以这种密度计的刻度是不均匀。
故答案为:1.0;9.6;不均匀,由表达式h液h可知,h液和ρ液是反比例函数。
8.(1)方法1:将这段木块竖直漂浮于水中,水面与木块相切处即为零刻度线位置
方法2:∵漂浮∴F浮=G木 又∵F浮=ρ水gV水,G木=ρ木gV木, ∴ρ水gSh=ρ木gSL,
∴h= = ,
离下表面竖直距离20cm处为零刻度线位置
(2)设距离上表面10厘米处的刻度对应的质量为m
F’浮= G水+mg
F’浮=ρ水gV’水=ρ水gSh’
=1.0×103kg/m3×10N/kg×0.1m2×(0.4-0.1)m=300N
G木=m木g=ρ木V木g=ρ木SLg
=0.5×103kg/m3×0.1m2×0.4m×10N/kg=200N
【解析】(1)根据m=ρV算出物体的质量即质量为0的刻度线的位置; (2)算出距离上表面10厘米排开水的质量减去木料的质量就是对应的质量。
9.解:
(1)杯子的重力:
G=mg=100×10﹣3kg×10N/kg=1N,
因为杯子漂浮在水面上,所以F浮=G=1N;
(2)当杯子下沉的深度为30cm=0.3m时,此时杯子受到的浮力最大,
F浮′=ρ水gV排′=1.0×103kg/m3×10N/kg×20×10﹣4m2×0.3m=6N,
最大物重G最大=F浮′﹣G=6N﹣1N=5N,
则此浮力秤的最大称量为:
m最大0.5kg。
答:(1)将杯子开口向上竖直放入水中时,杯子受到的浮力是1N。
(2)此时浮力秤的最大称量为0.5kg。
10.解:(1)根据题意知道,“小金将其放入水中,液面所在处标注为A”,所以,A处标注处的密度为水的密度,故示数应是1.0×103。
(2)该密度计的总重力:G=mg=27×10﹣3kg×10N/kg=0.27N
则图中密度计受到的浮力:F浮=G=0.27N
若将该密度计从水中取出擦干、放到密度为0.8×103kg/m3的酒精中,液体密度减小,但密度计仍然漂浮,浮力大小不变,仍然为0.27N,根据F浮=ρ液gV排知道,密度计排开液体的体积增大,露出水面的体积减小,所以,此时吸管上酒精液面的位置在A的上方。
密度计受到的浮力等于密度计的重力,不随着浸入深度的变化而变化,故该密度计在不同液体中所受浮力大小与浸入深度的关系图
(3)根据漂浮条件和据F浮=ρ液gV排知道,密度计漂浮在水中时所受浮力:F浮水=G
密度计漂浮在酒精中时所受浮力:F浮液体=G
所以F浮液体=F浮水
即ρ液体gSh液体=ρ水gSh水
故该液体的密度:0.9×103kg/m3
故答案为:(1)1.0×103;(2)上方;见上图;(3)此液体的密度0.9×103kg/m3。
11.解:(1)小筒底面积为10cm2,小筒浸入水中的长度为8cm,故小筒排开水的体积为V排=Sh=10cm2×8cm=80cm3=8×10﹣5m3
因小筒和秤盘是漂浮在水面上,故G筒=F浮=ρ液gV排=1.0×103kg/m3×10N/kg×8×10﹣5m3=0.8N;
(2)该秤测物体的最大质量时,就是V排=V筒=Sh=10cm2×20cm=200cm3=2×10﹣4m3
此时物体和小筒秤盘的总重力G=F浮=ρ液gV排=1.0×103kg/m3×10N/kg×2×10﹣4m3=2N
故此时物体的重力为G物=G﹣G筒=2N﹣0.8N=1.2N
此时物体的质量为m物0.12kg;
(3)根据以上分析可知物体质量m物;
因液体密度ρ液、小筒底面积S、小筒质量m筒都是定值,故物体质量与小筒浸入的深度是一次函数关系,故小筒上的刻度(即代表了小筒的深度)是均匀的。
答:(1)小筒和秤盘的总重力是0.8N;(2)能称出物体的最大质量是0.12kg;
(3)物体质量与小筒浸入的深度是一次函数关系,故小筒上的刻度(即代表了小筒的深度)是均匀的。
密度计、浮力秤
同课章节目录
