人教版数学八年级下册18.2.1矩形 课后练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.1矩形 课后练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 791.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 19:54:06 | ||
图片预览



文档简介
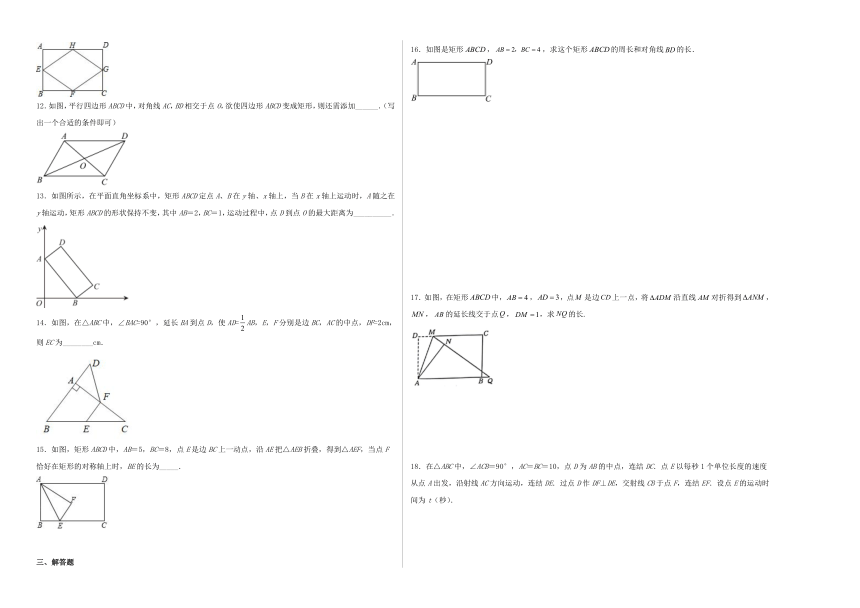
18.2.1 矩形 课后练习
一、单选题
1.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠A=∠C B.AB=BC C.AC⊥BD D.AC=BD
2.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A. B. C. D.
3.如图,把矩形纸片纸沿对角线折叠,设重叠部分为,那么下列说法错误的是( )
A.是等腰三角形 B.
C.折叠后得到的图形是轴对称图形 D.
4.一根长、宽的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后,,则最初折叠时,的长为( )
A. B. C. D.
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,BD=12,∠ACB=30°,则AB=( )
A.9 B.6 C.12 D.24
6.如图,矩形中,对角线、相交于点,若,,则矩形的对角线长为( )
A.2 B.4 C.6 D.8
7.如图,在中,、分别是直角边、的中点,若,则边上的中线的长为( )
A.5 B.6 C. D.10
8.如图,在中,,于点D,E为AB的中点,连接CE,若,,则的度数是( )
A.15° B.30° C.45° D.60°
9.一个矩形的两条对角线的夹角为 60°,且对角线的长度为 8cm,则较短边的长度为( )
A. B. C. D.
10.如图,中,,在上,为的中点,,相交于,且,若,则( )
A. B. C. D.
二、填空题
11.如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点则四边形EFGH的周长等于___cm.
12.如图,平行四边形ABCD中,对角线AC,BD相交于点O,欲使四边形ABCD变成矩形,则还需添加______.(写出一个合适的条件即可)
13.如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为__________.
14.如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点,DF=2cm,则EC为________cm.
15.如图,矩形ABCD中,AB=5,BC=8,点E是边BC上一动点,沿AE把△AEB折叠,得到△AEF,当点F恰好在矩形的对称轴上时,BE的长为_____.
三、解答题
16.如图是矩形,,求这个矩形的周长和对角线的长.
17.如图,在矩形中,,,点是边上一点,将沿直线对折得到,,的延长线交于点,,求的长.
18.在△ABC中,∠ACB=90°,AC=BC=10,点D为AB的中点,连结DC.点E以每秒1个单位长度的速度从点A出发,沿射线AC方向运动,连结DE.过点D作DF⊥DE,交射线CB于点F,连结EF.设点E的运动时间为t(秒).
(1)如图,当0<t<10时.
①求证:∠ADE=∠CDF;
②试探索四边形CEDF的面积是否为定值?若为定值,求出这个定值;若不为定值,请说明理由;
(2)当t≥10时,试用含t的代数式表示△DEF的面积.
19.已知:如图,在矩形ABCD中,E、F分是边BC、AB上的点,且EF=ED,EF⊥ED.
(1)请问BE与CD有什么数量关系,为什么?
(2)求证:AE平分∠BAD.
20.如图,中,,,,,点从点出发,以的速度向点运动;点从点同时出发,以的速度向点运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为秒.
(1)当为何值时,四边形是矩形?
(2)当为何值时,?为什么?
参考答案
1.D
2.C
3.B
4.C
5.B
6.B
7.D
8.B
9.C
10.C
11.16.
12.AC=BD(答案不唯一)
13.+1
14.2
15.或
16.解:如图所示,连接,
∵四边形是矩形,,
∴,这个矩形的周长为,
∴.
17.解:∵,
又∵,,
∴,
设,则,
在中,
∵,
∴,
解得,
即.
18.证明:(1)①∵AC=BC,点D为AB的中点,
∴CD⊥AB,
∵DF⊥DE,
∴∠ADE+∠CDE=∠CDF+∠CDE=90°,
∴∠ADE=∠CDF;
②结论:四边形CEDF的面积为定值,理由如下:
∵AC=BC,点D为AB的中点,∠ACB=90°,
∴∠A=∠B=∠ACD=∠BCD=45°,,
∴AD=BD=CD,
∵∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ACD=.
∴四边形CEDF的面积为定值.
(2)
解:当t≥10时,点E在AC的延长线上.
过点D分别作DG⊥BC,DH⊥AC,垂足分别为点G,H.
∵∠FDC=∠FDE+∠CDE=∠BDC+∠BDF,
∴∠BDF=∠CDE.
由②得:AD=BD=CD,∠ABC=∠ACD=45°,
∴∠DBF=∠DCE=135°,
∴△DBF≌△DCE(ASA),
∴BF=CE=t﹣10,
∴CF=CB+BF=10+(t﹣10)=t.
∵ ,DG⊥BC,DH⊥AC,
∴ ,
∵AD=BD=CD,AC=BC=10,
∴DG=DH=5.
∵=,
∴.
19. (1)解:BE=CD,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD.
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
在△EBF和△DCE中,
,
∴△EBF≌△DCE(AAS).
∴BE=CD;
(2)证明:∵AB=CD,BE=CD,
∴BE=AB,
∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.
20(1)解:由题意得,PD=2t,BQ=24-3t,
当PD=BQ时,2t=24-3t,解得t=,
又∵,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
即当t=s时,四边形是矩形.
(2)
当s或6s时,.
①如图1,过点P作PM⊥BC于点M,过点E作EN⊥BC于点N,
∴PMEN,∠PMN=∠PMB=∠ENB=∠CNE=90°,
∵DEBC,
∴∠DPM=∠DEN=∠MPE=90°,PM=EN,
∴四边形BMPD、四边形DENB都是矩形,
∴,BN=DE=18cm,BM=PD=2t,
∴CN=BC-BN=6cm,
∵PQ=CE,
∴Rt△PMQ≌Rt△ENC(HL),
∴MQ=NC,
∵BQ-BM-CQ=CN,
∴24-2t-3t=6,
解得,
即当s时,PQ=CE;
②如图2,过点P作PM⊥BC于点M,过点E作EN⊥BC于点N,
由①可知,四边形DPMB、四边形DENB都是矩形,
∴PM=EN,BM=PD=2t,BN=DE=18cm,MN=PE=18-2t,
∴CN=BC-BN=6cm,
∵PQ=CE,
∴Rt△PMQ≌Rt△ENC(HL),
∴MQ=NC,
∵BM-BQ=CN,
∴2t-(24-3t)=6,
解得t=6,
即当t=6s时,.
综上所述,即当s或6s时,.
一、单选题
1.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠A=∠C B.AB=BC C.AC⊥BD D.AC=BD
2.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A. B. C. D.
3.如图,把矩形纸片纸沿对角线折叠,设重叠部分为,那么下列说法错误的是( )
A.是等腰三角形 B.
C.折叠后得到的图形是轴对称图形 D.
4.一根长、宽的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后,,则最初折叠时,的长为( )
A. B. C. D.
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,BD=12,∠ACB=30°,则AB=( )
A.9 B.6 C.12 D.24
6.如图,矩形中,对角线、相交于点,若,,则矩形的对角线长为( )
A.2 B.4 C.6 D.8
7.如图,在中,、分别是直角边、的中点,若,则边上的中线的长为( )
A.5 B.6 C. D.10
8.如图,在中,,于点D,E为AB的中点,连接CE,若,,则的度数是( )
A.15° B.30° C.45° D.60°
9.一个矩形的两条对角线的夹角为 60°,且对角线的长度为 8cm,则较短边的长度为( )
A. B. C. D.
10.如图,中,,在上,为的中点,,相交于,且,若,则( )
A. B. C. D.
二、填空题
11.如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点则四边形EFGH的周长等于___cm.
12.如图,平行四边形ABCD中,对角线AC,BD相交于点O,欲使四边形ABCD变成矩形,则还需添加______.(写出一个合适的条件即可)
13.如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为__________.
14.如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点,DF=2cm,则EC为________cm.
15.如图,矩形ABCD中,AB=5,BC=8,点E是边BC上一动点,沿AE把△AEB折叠,得到△AEF,当点F恰好在矩形的对称轴上时,BE的长为_____.
三、解答题
16.如图是矩形,,求这个矩形的周长和对角线的长.
17.如图,在矩形中,,,点是边上一点,将沿直线对折得到,,的延长线交于点,,求的长.
18.在△ABC中,∠ACB=90°,AC=BC=10,点D为AB的中点,连结DC.点E以每秒1个单位长度的速度从点A出发,沿射线AC方向运动,连结DE.过点D作DF⊥DE,交射线CB于点F,连结EF.设点E的运动时间为t(秒).
(1)如图,当0<t<10时.
①求证:∠ADE=∠CDF;
②试探索四边形CEDF的面积是否为定值?若为定值,求出这个定值;若不为定值,请说明理由;
(2)当t≥10时,试用含t的代数式表示△DEF的面积.
19.已知:如图,在矩形ABCD中,E、F分是边BC、AB上的点,且EF=ED,EF⊥ED.
(1)请问BE与CD有什么数量关系,为什么?
(2)求证:AE平分∠BAD.
20.如图,中,,,,,点从点出发,以的速度向点运动;点从点同时出发,以的速度向点运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为秒.
(1)当为何值时,四边形是矩形?
(2)当为何值时,?为什么?
参考答案
1.D
2.C
3.B
4.C
5.B
6.B
7.D
8.B
9.C
10.C
11.16.
12.AC=BD(答案不唯一)
13.+1
14.2
15.或
16.解:如图所示,连接,
∵四边形是矩形,,
∴,这个矩形的周长为,
∴.
17.解:∵,
又∵,,
∴,
设,则,
在中,
∵,
∴,
解得,
即.
18.证明:(1)①∵AC=BC,点D为AB的中点,
∴CD⊥AB,
∵DF⊥DE,
∴∠ADE+∠CDE=∠CDF+∠CDE=90°,
∴∠ADE=∠CDF;
②结论:四边形CEDF的面积为定值,理由如下:
∵AC=BC,点D为AB的中点,∠ACB=90°,
∴∠A=∠B=∠ACD=∠BCD=45°,,
∴AD=BD=CD,
∵∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),
∴S△ADE=S△CDF,
∴S四边形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ACD=.
∴四边形CEDF的面积为定值.
(2)
解:当t≥10时,点E在AC的延长线上.
过点D分别作DG⊥BC,DH⊥AC,垂足分别为点G,H.
∵∠FDC=∠FDE+∠CDE=∠BDC+∠BDF,
∴∠BDF=∠CDE.
由②得:AD=BD=CD,∠ABC=∠ACD=45°,
∴∠DBF=∠DCE=135°,
∴△DBF≌△DCE(ASA),
∴BF=CE=t﹣10,
∴CF=CB+BF=10+(t﹣10)=t.
∵ ,DG⊥BC,DH⊥AC,
∴ ,
∵AD=BD=CD,AC=BC=10,
∴DG=DH=5.
∵=,
∴.
19. (1)解:BE=CD,理由如下:
∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,AB=CD.
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠BEF+∠CED=90°.
∴∠BFE=∠CED.
在△EBF和△DCE中,
,
∴△EBF≌△DCE(AAS).
∴BE=CD;
(2)证明:∵AB=CD,BE=CD,
∴BE=AB,
∴∠BAE=∠BEA=45°.
∴∠EAD=45°.
∴∠BAE=∠EAD.
∴AE平分∠BAD.
20(1)解:由题意得,PD=2t,BQ=24-3t,
当PD=BQ时,2t=24-3t,解得t=,
又∵,
∴四边形是平行四边形,
∵,
∴四边形是矩形,
即当t=s时,四边形是矩形.
(2)
当s或6s时,.
①如图1,过点P作PM⊥BC于点M,过点E作EN⊥BC于点N,
∴PMEN,∠PMN=∠PMB=∠ENB=∠CNE=90°,
∵DEBC,
∴∠DPM=∠DEN=∠MPE=90°,PM=EN,
∴四边形BMPD、四边形DENB都是矩形,
∴,BN=DE=18cm,BM=PD=2t,
∴CN=BC-BN=6cm,
∵PQ=CE,
∴Rt△PMQ≌Rt△ENC(HL),
∴MQ=NC,
∵BQ-BM-CQ=CN,
∴24-2t-3t=6,
解得,
即当s时,PQ=CE;
②如图2,过点P作PM⊥BC于点M,过点E作EN⊥BC于点N,
由①可知,四边形DPMB、四边形DENB都是矩形,
∴PM=EN,BM=PD=2t,BN=DE=18cm,MN=PE=18-2t,
∴CN=BC-BN=6cm,
∵PQ=CE,
∴Rt△PMQ≌Rt△ENC(HL),
∴MQ=NC,
∵BM-BQ=CN,
∴2t-(24-3t)=6,
解得t=6,
即当t=6s时,.
综上所述,即当s或6s时,.
