【备考2023】浙教版科学中考“临阵磨枪”专题训练(十七):浮力、压强的计算【word,含解析】
文档属性
| 名称 | 【备考2023】浙教版科学中考“临阵磨枪”专题训练(十七):浮力、压强的计算【word,含解析】 |  | |
| 格式 | doc | ||
| 文件大小 | 599.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-04-07 10:23:52 | ||
图片预览



文档简介
1.2021年11月13日,全球200多个国家达成了《格拉斯哥气候公约》,一致决定在未来减少碳排放,缓解全球气候变暖。全球气候变暖会导致南极洲冰川(为淡水冰川)大面积熔化,海面上出现大量浮冰,现有一块质量51吨的浮冰漂浮在海面上,若当地海域海水的密度为1.02×103kg/m3,浮冰的密度为0.9×103kg/m3。请解决下列问题:
(1)浮冰受到的浮力是多少?
(2)浮冰在海面以下的体积是多少?
(3)如果海面所有浮冰全部熔化后,请结合相关公式推理说明是否会对海平面水位造成影响。
(4)为了缓解全球变暖,社会开始倡导节能、低碳的生活方式,请你给出一条生活中的建议。
2.在水平地面上放置一圆柱形容器,内装一定深度的水,将一个质量为0.4kg、体积为5×10﹣3m3的不吸水的塑料块A放入水中,其状态如图甲所示。在塑料块上方放一石块B,最终使得塑料块A上口边缘与水面相平,如图乙所示,求:(g=10N/kg,水的密度ρ=1.0×103kg/m3)
(1)塑料块受到的浮力;
(2)石块B的重力。
3.周末,小明随爸爸去郊外钓鱼时,观察到爸爸在钓鱼前要通过“试漂”来确定铅坠(铅坠由合金制成)的大小,尽量使“浮标”灵敏,图中是浮标和铅坠的位置示意图。若球形浮标的体积为15cm3,铅坠的密度为ρ铅=11g/cm3。(取水的密度ρ水=1.0×103kg/m3,g=10N/kg)
(1)有经验的钓鱼者会使浮标体积的三分之一露出水面,此时浮标受到的浮力是多大?
(2)小明看见爸爸有一种体积为0.5cm3的铅坠,这种铅坠受到的重力为多少?
(3)如果使用这种铅坠,浮标静止时浸入水中的体积是多大?(设:铅坠末接触池底,浮标的质量、钓线、鱼钩、鱼饵的体积及质量均不计)
4.疫情期间,全国很多地方实行疫区封闭管理,使用无人机进行常态化安全巡查,如图所示。无人机起飞前,放在地面上要确保脚架平稳着地;启动后,利用遥控器可控制它运动和工作。该无人机的部分参数如下表。
机身尺寸(毫米) 400×300×200
机身质量(千克) 25
飞机着地总面积(厘米2) 10
最大载物量(千克) 10
(1)无人机利用携带的焦距一定的微型摄像机进行航拍,来自地面景物的光通过摄像机镜头,会聚在感光晶片上,形成倒立、 (选填“放大”或“缩小”)的实像;当无人机下降时,须 (选填“增大”或“减小”)镜头与感光晶片间的距离,才能拍摄到清晰的画面。
(2)无人机匀速降落过程中,其所受重力G和升力F的大小关系为 。
(3)该无人机空载停放在地面上时,对地面产生的压强为多少?(写出计算过程)
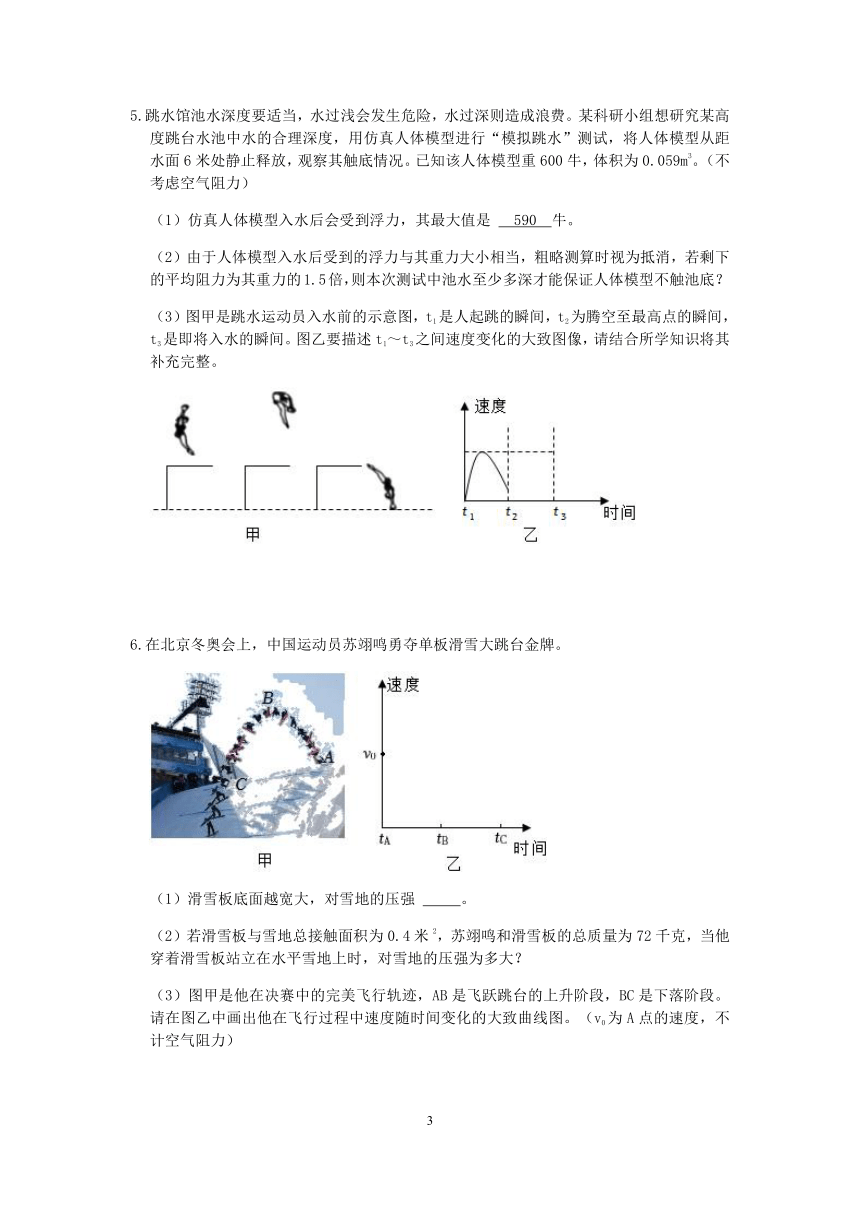
5.跳水馆池水深度要适当,水过浅会发生危险,水过深则造成浪费。某科研小组想研究某高度跳台水池中水的合理深度,用仿真人体模型进行“模拟跳水”测试,将人体模型从距水面6米处静止释放,观察其触底情况。已知该人体模型重600牛,体积为0.059m3。(不考虑空气阻力)
(1)仿真人体模型入水后会受到浮力,其最大值是 590 牛。
(2)由于人体模型入水后受到的浮力与其重力大小相当,粗略测算时视为抵消,若剩下的平均阻力为其重力的1.5倍,则本次测试中池水至少多深才能保证人体模型不触池底?
(3)图甲是跳水运动员入水前的示意图,t1是人起跳的瞬间,t2为腾空至最高点的瞬间,t3是即将入水的瞬间。图乙要描述t1~t3之间速度变化的大致图像,请结合所学知识将其补充完整。
6.在北京冬奥会上,中国运动员苏翊鸣勇夺单板滑雪大跳台金牌。
(1)滑雪板底面越宽大,对雪地的压强 。
(2)若滑雪板与雪地总接触面积为0.4米2,苏翊鸣和滑雪板的总质量为72千克,当他穿着滑雪板站立在水平雪地上时,对雪地的压强为多大?
(3)图甲是他在决赛中的完美飞行轨迹,AB是飞跃跳台的上升阶段,BC是下落阶段。请在图乙中画出他在飞行过程中速度随时间变化的大致曲线图。(v0为A点的速度,不计空气阻力)
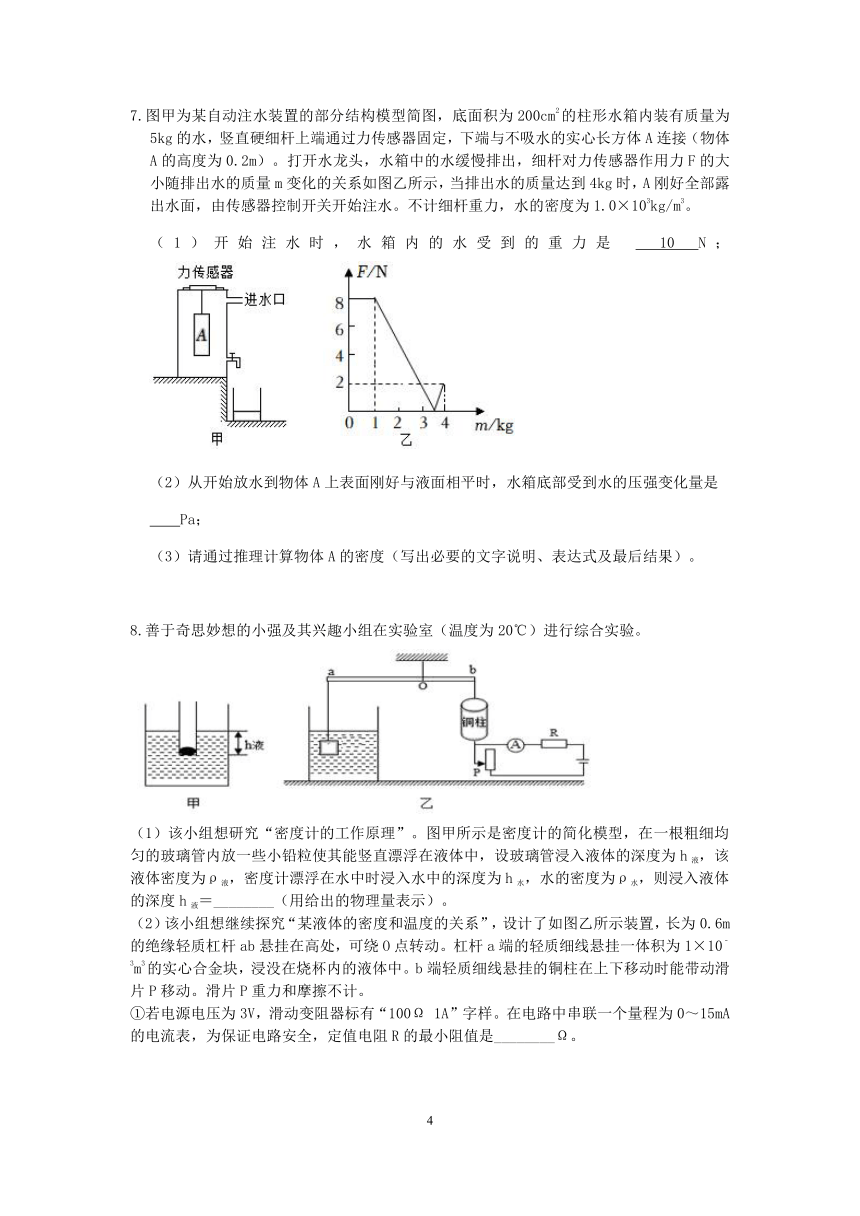
7.图甲为某自动注水装置的部分结构模型简图,底面积为200cm2的柱形水箱内装有质量为5kg的水,竖直硬细杆上端通过力传感器固定,下端与不吸水的实心长方体A连接(物体A的高度为0.2m)。打开水龙头,水箱中的水缓慢排出,细杆对力传感器作用力F的大小随排出水的质量m变化的关系如图乙所示,当排出水的质量达到4kg时,A刚好全部露出水面,由传感器控制开关开始注水。不计细杆重力,水的密度为1.0×103kg/m3。
(1)开始注水时,水箱内的水受到的重力是 10 N;
(2)从开始放水到物体A上表面刚好与液面相平时,水箱底部受到水的压强变化量是
Pa;
(3)请通过推理计算物体A的密度(写出必要的文字说明、表达式及最后结果)。
8.善于奇思妙想的小强及其兴趣小组在实验室(温度为20℃)进行综合实验。
(1)该小组想研究“密度计的工作原理”。图甲所示是密度计的简化模型,在一根粗细均匀的玻璃管内放一些小铅粒使其能竖直漂浮在液体中,设玻璃管浸入液体的深度为h液,该液体密度为ρ液,密度计漂浮在水中时浸入水中的深度为h水,水的密度为ρ水,则浸入液体的深度h液=________(用给出的物理量表示)。
(2)该小组想继续探究“某液体的密度和温度的关系”,设计了如图乙所示装置,长为0.6m的绝缘轻质杠杆ab悬挂在高处,可绕O点转动。杠杆a端的轻质细线悬挂一体积为1×10﹣3m3的实心合金块,浸没在烧杯内的液体中。b端轻质细线悬挂的铜柱在上下移动时能带动滑片P移动。滑片P重力和摩擦不计。
①若电源电压为3V,滑动变阻器标有“100Ω 1A”字样。在电路中串联一个量程为0~15mA的电流表,为保证电路安全,定值电阻R的最小阻值是________Ω。
②小强在给该液体加热过程中发现,电流表示数减小,则可得出该液体的密度随温度升高而________(选填“增大”、“减小”或“不变”)(除烧杯内的液体外,装置中其他物体的热胀冷缩忽略不计,合金块始终浸没)。
(3)该小组还想利用此装置继续测量该合金块的密度。已知该烧杯中液体在温度为20℃时计的密度为1.1×103kg/m3。杠杆水平平衡时,铜柱质量为2kg,点O距杠杆b端0.2m。则的密度是________kg/m3(g取10N/kg)
9.一个底面积为10m2的圆柱状容器,装有适量的水,现在将一个体积为20m3、密度为0.8×103kg/m3的物体A放入其中,最终物体A漂浮于水面上。
则:
(1)物体A所受到的浮力是多少?
(2)如图所示,若将画斜线部分截取下来并取出(其体积为浸入水中体积的一半),则取出的那部分物体的质量是多少?
(3)待剩余部分再次静止后,容器底部受到压强减小了多少?(g=10N/kg)
10.一个圆柱形容器放在水平桌面上,在容器中放着一个密度小于水的均匀圆柱体M,且圆柱体M通过细线与圆柱形容器底部相连,如图甲所示(细线未画出)。现慢慢向容器中加水,圆柱形容器内水面高度为h,如图乙所示。测得水面高度h与所加水的质量m的关系如图丙所示。所加水量在3kg以内的过程中无水溢出。(图甲图乙中圆柱体和容器大小,以及细绳的长度不具有暗示意义)求:
(1)由甲图可知圆柱体M刚好漂浮时容器中水的深度h=8cm,请回答圆柱体M的高度H=________ cm。
(2)圆柱体M的密度;
(3)圆柱体M的的重力;
11.如图甲,水平升降台上有一圆柱形容器,容器中装有一定量的水,现将一实心正方体M(不吸水)悬挂在不可伸缩的细绳下端(细绳体积忽略不计),使M浸没水中并刚好与容器底接触但不产生压力,现使升降台匀速下降,图乙是绳的拉力F随时间t的变化图象。
(1)在t1和 t2时刻,M所受浮力分别为F浮1、F浮2,则 F浮1________F浮2(选填“>”、“<”或“=”)。
(2)求物体M的密度。
(3)当绳子的拉力为0.63N时,正方体上表面到水面的距离。
答案及解析
1.解:(1)浮冰的重力:
G冰=mg=51×103kg×10N/kg=5.1×105N;
由于浮冰漂浮:
则:F浮=G冰=5.1×105N;
(2)根据阿基米德原理可知,浮冰在海面以下的体积V排50m3;
(3)因为浮冰漂浮于海面上,
所以F浮=ρ海水gV排=G冰,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
又因为冰熔化成水后,其质量不变,重力不变,
所以G水=ρ水gV水=G冰,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
由①②可得:ρ海水gV排=ρ水gV水,
所以V排<V水,
即:浮冰熔化为水的体积大于浮冰排开水的体积。
所以浮冰全部熔化后,海平面水位上升;
(4)绿色出行。
答:(1)浮冰受到的浮力是5.1×105N;
(2)浮冰在海面以下的体积是50m3;
(3)如果海面所有浮冰全部熔化后,海平面水位上升;
(4)绿色出行。
2.解:(1)塑料块处于漂浮状态,所以所受浮力为:F浮1=GA=mAg=0.4kg×10N/kg=4N;
(2)图乙塑料块A上口边缘与水面相平,V排=VA=5×10﹣3m3,此时A受到的浮力为:F浮2=ρ水V排g=1.0×103kg/m3×5×10﹣3m3×10N/kg=50N;
图乙中物体的受力关系为:F浮2=GA+GB,
所以石块B的重力为:GB=F浮2﹣GA=50N﹣4N=46N。
答:(1)塑料块受到的浮力为4N;
(2)石块B的重力为46N。
3.解:(1)浮标有的体积露出水中时:
则浮标浸入水中的体积:V排V浮标15cm3=10cm3;
此时浮标受到的浮力为F浮=ρ水gV排=1.0×103 kg/m3×10N/kg×10×10﹣6m3=0.1N;
(2)这种铅坠质量为m=ρV=11g/cm3×0.5cm3=5.5g=5.5×10﹣3kg;
受到的重力为G=mg=5.5×10﹣3kg×10N/kg=0.055N;
(3)由于铅坠未接触池底,浮标和铅坠静止时受到的浮力:
F浮′=G总=0.055N,
根据F浮=ρ水gV排可得,此时排开水的体积:
V排′5.5×10﹣6m3=5.5cm3;
浮标浸入水中的体积
V浸=V排′﹣V=5.5cm3﹣0.5cm3=5cm3;
答:(1)此时浮标受到的浮力是0.1N;
(2)这种铅坠受到的重力为0.055N;
(3)浮标静止时浸入水中的体积为5cm3。
4.解:(1)摄像机的镜头相当于一个凸透镜,其成像的原理是:当物距大于二倍焦距时,凸透镜成倒立缩小的实像;
当无人机下降时,物距减小,像距变大,需增大镜头与感光晶片的距离,才能拍摄到清晰的画面;
(2)无人机匀速降落过程中,无人机处于平衡运动状态,螺旋桨产生的升力等于重力;
(3)无人机空载停放在地面上时对水平面的压力为:
F压=G=mg=25kg×10N/kg=250N,
对地面产生的压强为:
p2.5×105Pa。
故答案为:(1)缩小;增大;(2)重力G等于升力F;(3)该无人机空载停放在地面上时,对地面产生的压强为2.5×106Pa。
5.解:(1)由浮力公式F浮=ρ水gV排可得浮力的最大值是:
F浮=ρ水gV排=ρ水gV=1.0×103kg/m3×10N/kg×0.059m3=590N;
(2)由机械能守恒定律知,动能的大小就是重力势能的减小量,入水后,依据题意,人体模型受到的浮力与其重力大小相当,视为抵消,仅受向上的阻力为1.5mg,
由动能定理可得:mgh=1.5mgdmin,
可得池水深度至少是:dmin4m;
(3)t2~t3期间,运动员做自由落体运动,因为运动员仅受重力,故合外力不变,加速度不变,故斜率不变。如图所示:
故答案为:(1)590;(2)本次测试中池水至少4m深才能保证人体模型不触池底;(3)见解答图。
6.解:(1)压强的大小与压力大小和受力面积大小有关,所以滑雪板底面越宽大,在压力相同的情况下,由于受力面积越大,所以 滑雪板对雪地的压强越小;
(2)苏翊鸣和滑雪板的总重力:G=mg=72kg×10N/kg=720N;
当他穿着滑雪板站立在水平雪地上时,对雪地的压力F=G=720N;
对雪地的压强:p1800Pa;
(3)他在飞行过程中,上升阶段:动能转化为重力势能,动能减小,速度减小;下落阶段:重力势能转化为动能,动能增大,速度增大;
所以他在整个过程中的速度先变小,当上升到最高点B时,速度最小,接着下落过程速度变大;
速度随时间变化的大致曲线图如图所示:
答:(1)越小;
(2)当他穿着滑雪板站立在水平雪地上时,对雪地的压强为1800Pa;
(3)图见解析。
7.解:(1)水箱内剩余水的重力为:G剩=m剩g=(5kg﹣4kg)×10N/kg=10N;
(2)根据题意和图像可知,从开始放水到物体A上表面刚好与液面相平时,放出水的质量为1kg,
该过程中物体A始终浸没在水中,则物体A受到的浮力大小不变,
又因为水对水箱底部的压力:F=G水+F浮,
所以,该过程中水对水箱底部的压力变化量为:ΔF=ΔG水=G排水=m排水g=1kg×10N/kg=10N,
则水箱底部受到水的压强变化量为:Δp500Pa。
(3)由图乙可知,在排水量为0~1kg范围内,F不变,A受到细杆对它竖直向下的压力和重力以及竖直向上的浮力作用且F浮=F+G,A处于浸没状态,即VA=V排,排水前A上表面上方水的质量为1kg;
在F从零增大到2N的范围内,A受到竖直向下的重力和竖直向上的浮力、细杆对A竖直向上的拉力的作用,
且G=F+F浮,在排水量为4kg时,A受到的浮力为零,即GA=F拉=2N;
当A完全浸没时受到的浮力为:F浮=GA+F压=2N+8N=10N,
A的体积为:VA=V排10 3m3,
A的密度为:ρA0.2×103kg/m3;
故答案为:(1)10;
(2)500;
(3)物体A的密度为0.2×103kg/m3,推理过程见解析。
8.(1)ρ水h水/ρ液
(2)200;减小
(3)2.1x103
【解析】(1)密度计始终在液面漂浮,根据浮沉条件可知,它在水中受到的浮力和在液体中受到的浮力相等,据此列出等式,并用阿基米德原理将等式拆开,带入数据计算即可;
(2)①为了保证电流表的安全,当变阻器的阻值为零时,电流也不能超过量程,根据计算定值电阻的最小阻值;
②首先根据电流表的示数变化分析变阻器阻值的变化,进而推断出滑片的移动方向,再确定杠杆的旋转方向,接下来根据杠杆的旋转方向确定a端物体受到浮力的变化,最后根据阿基米德原理确定液体密度的变化。
(3)首先根据杠杆的平衡条件计算出a端合金块受到的拉力,然后根据G=F浮+F拉列出等式,用密度公式和阿基米德原理将等式拆开,最后推导计算合金块的密度即可。
【解答】(1)密度计始终漂浮在液面上,
那么F浮水=F浮液;
ρ水gV排水=ρ液gV排液
ρ水V排水=ρ液V排液
ρ水Sh水=ρ液Sh液;
ρ水h水=ρ液h液;
解得:;
(2)①定值电阻的最小阻值为:。
②电流表的示数变小,那么变阻器的阻值增大,即铜柱向上移动,则左端合金块下沉,说明合金块受到的拉力增大了。根据G=F浮+F拉可知,合金块受到的浮力减小了。根据阿基米德原理F浮=ρ液gV排可知,合金块的V排不变,那么液体密度变小了。因此液体的密度随温度升高而减小。
(3)根据杠杆的平衡条件得到:G铜×OB=F拉×OA;
2kg×10N/kg×0.2m=F拉×(0.6m-0.2m);
解得:F拉=10N;
根据二力平衡的知识得到:G=F浮+F拉;
ρgV=ρ液gV+10N;
ρ×10N/kg× 1×10﹣3m3 = 1.1×103kg/m3 ×10N/kg× 1×10﹣3m3+10N;
解得:ρ= 2.1x103 kg/m3 。
9.(1)由题意可知:物体A的密度ρA=0.8×103kg/m3,体积VA=20m3,质量mA=ρAVA=0.8×103kg/m3×20m3=1.6×104kg,则GA=mAg=1.6×104kg×10N/kg=1.6×105N.
∵物体A漂浮于水面上,∴物体A所受的浮力F浮=GA=1.6×105N
(2)由F浮=ρ水gV排得:
取出的那部分物体的体积V′= V排= ×16m3=8m3,质量为m′=ρAV′=0.8×103kg/m3×8m3=6.4×103kg。根据取出的那部分物体的重力G′=m′g=6.4×103kg×10N/kg=6.4×104N.S=10m2,则压力的改变量△F=G′=6.4×104N
(3)容器底部受到压强减小了
【解析】1、根据浮沉条件,物体A的密度小于水的密度,所以物体A在水中处于漂浮状态,浮力等于物体A的重力。由物体的密度和体积求出物体的质量,再根据公式G=mg;
2、根据浮力公式变形得可以求出浸在水中的物体A的体积,可求出1/2体积的大小,再由可求出截取部分物体的质量;
3、截取部分漂浮的物体后,液体对容器底部的压力减小了,减小的这部分压力数值上等于截取部分物体的重力,根据压力的减小值可以计算出压强的减小值。
10.(1)10
(2)当圆柱体飘浮时:F浮=G
ρ水gSh高=ρ物gSH 1000kg/m3×gS×0.08m=×ρ物gS×0.1m
得ρ物=800kg/m3
(3)由图得,当容器内水的深度从8cm到12cm时,
水的体积增加量:△V=△m/ρ水=1kg/1000kg/m3=0.001m3
在这个过程中,圆柱体一直处于漂浮状态,即S容=△V/△h=0.001m3/0.04m=0.025m2
由图得,当容器内水的深度从0cm到8cm时,
水的体积增加量:△V’=△m’/ρ水=0.8kg/1000kg/m3=0.0008m3
在圆柱体漂浮前,S容-S圆=△V’/△h’=0.0008m3/0.08m=0.01m2
即S圆=0.015m2
G=ρ物gS圆H=800kg/m3×10N/kg×0.015m2×0.08m=12N
【解析】在开始的一段时间内,M受到的浮力小于重力,它在容器底部静止不动,此时由于它占有部分体积,所以水面高度上升的较快;当水面高度达到8cm时,M受到的浮力等于重力,它开始在水面漂浮,随着水面的上升而上升;当水面高度达到12cm时,下面的细线被拉直,M不再上升;当水面高度达到14cm时,M被完全淹没,此后水面不断上升,而M的位置则保持不变;
(1)从图中找到木块刚好漂浮时水面的高度,以及细线被拉直时到M完全淹没时的水面高度变化,然后二者相加就是M的高度H;
(2)当M刚好漂浮时,水面的高度为8cm,根据漂浮条件列出浮力和重力的关系式,用阿基米德原理和密度公式将二者分解计算即可;
(3) 根据图甲可知,当容器内水的深度从8cm到12cm时, M处于漂浮状态,跟随水面不断上升。确定此段时间内加入水的质量,然后根据密度公式计算出加入水的体积V水,再根据计算出容器的底面积。
当容器内水的深度从0cm到8cm时, M在容器底部保持不动。根据图片确定这段时间内加入水的质量 △m ',根据密度公式计算出加入水的体积 △V ',再根据△S'= △V'/△h’计算出容器的底面积和M的底面积之差,接下来根据 S容-S圆= △S'计算出M的底面积,最后根据公式 G=m物g=ρ物gS圆H计算即可。
【解答】(1)根据图甲可知,木块刚好漂浮时水面的高度8cm,细线被拉直时到M完全淹没时的水面高度变化:14cm-12cm=2cm,那么圆柱体M的高度为:H=8cm+2cm=10cm。
(2)当圆柱体飘浮时,浮力等于重力,
即F浮=G;ρ水gSh高=ρ物gSH ;
1000kg/m3×gS×0.08m=×ρ物gS×0.1m;
解得:ρ物=800kg/m3。
(3)由图得,当容器内水的深度从8cm到12cm时,
水的体积增加量:△V=△m/ρ水=1kg/1000kg/m3=0.001m3;
在这个过程中,圆柱体一直处于漂浮状态,即S容=△V/△h=0.001m3/0.04m=0.025m2;
由图得,当容器内水的深度从0cm到8cm时,
水的体积增加量:△V’=△m’/ρ水=0.8kg/1000kg/m3=0.0008m3;
在圆柱体漂浮前,加入水的底面积△S'=△V’/△h’=0.0008m3/0.08m=0.01m2;
因为S容-S圆=△S';
那么S圆=S容-△S'=0.025m2-0.01m2=0.015m2;
圆柱体M的重力:G=m物g=ρ物gS圆H=800kg/m3×10N/kg×0.015m2×0.08m=12N。
11.(1)>
(2)G=0.81N
m= ==0.081kg
F浮=G-F拉=0.81N-0.54N=0.27N
∵浸没
∴V排=V物
∴F浮=ρ液gV排=ρ液gV物
V物= ==2.7x10-5m3
ρ===3×103kg/m3
(3)F浮'=G-F拉=0.81N-0.63N=0.18N
=2:3
设正方体边长为a,
上表面距离水面高度为h
V物=2.7x10-5m3=a3
a=0.03m
h= ·h=0.01m
【解析】根据乙图可知,在物体露出水面前,它排开水的体积等于自身体积,因此浮力保持不变,根据F=G-F浮可知,绳子的拉力保持不变;从开始露出水面到完全露出水面的过程中,物体排开水的体积不断减小,浮力不断减小,那么绳子的拉力不断增大。当物体完全露出水面后,物体不受浮力,此时绳子的拉力等于物体的重力,保持不变。
(1)首先根据乙图确定两个时刻时物体M受到拉力的大小关系,然后根据F浮=G-F比较两个时刻时受到浮力的大小关系;
(2)根据乙图,确定物体的重力和完全浸没时绳子的拉力,根据 F浮=G-F拉 计算出浸没时受到的浮力,根据 计算物体的体积,最后根据计算物体的密度。
(3)首先根据 F浮’=G-F拉 计算出此时物体受到的浮力,然后根据浮力与V排成正比,计算出此时V排和物体完全浸没时体积的比值,进而得到露出水面的体积和物体体积的比值。因为物体为长方体,所以两个体积之比等于上表面到水面高度与正方体边长的比,最后带入正方体的边长计算即可。
【解答】(1)根据图乙可知,t1时刻的拉力小于t2时刻的拉力,根据F浮=G-F可知,t1时刻的浮力大于t2时刻的浮力,即F浮1>F浮2;
(2)根据乙图可知,当物体完全出水后拉力F=0.81N,
根据二力平衡的知识得到,物体M的重力G=F=0.81N;
那么物体M的质量为: ;
当物体M完全浸没时受到的拉力为0.54N,
那么此时受到的浮力F浮=G-F拉=0.81N-0.54N=0.27N;
∵因为物体完全浸没在水中,
∴所以排开水的体积等于物体的体积,即V排=V物;
根据阿基米德原理F浮=ρ液gV排=ρ液gV物得到:
物体的体积;
物体的密度=。
(3)当绳子的拉力为0.63N时受到的浮力 F浮'=G-F拉=0.81N-0.63N=0.18N;
根据阿基米德原理F浮=ρ液gV排可知,当液体密度相同时,浮力与V排成正比,得到:
;
因为V物=V排'+V露,
那么:;
设正方体边长为a,上表面距离水面高度为h,
那么正方体上表面到水面的距离与物体的边长之比:;
根据V物=2.7x10-5m3=a3得到:
物体M的边长a=0.03m;
那正方体上表面到水面的距离。
浮力、压强的计算
(1)浮冰受到的浮力是多少?
(2)浮冰在海面以下的体积是多少?
(3)如果海面所有浮冰全部熔化后,请结合相关公式推理说明是否会对海平面水位造成影响。
(4)为了缓解全球变暖,社会开始倡导节能、低碳的生活方式,请你给出一条生活中的建议。
2.在水平地面上放置一圆柱形容器,内装一定深度的水,将一个质量为0.4kg、体积为5×10﹣3m3的不吸水的塑料块A放入水中,其状态如图甲所示。在塑料块上方放一石块B,最终使得塑料块A上口边缘与水面相平,如图乙所示,求:(g=10N/kg,水的密度ρ=1.0×103kg/m3)
(1)塑料块受到的浮力;
(2)石块B的重力。
3.周末,小明随爸爸去郊外钓鱼时,观察到爸爸在钓鱼前要通过“试漂”来确定铅坠(铅坠由合金制成)的大小,尽量使“浮标”灵敏,图中是浮标和铅坠的位置示意图。若球形浮标的体积为15cm3,铅坠的密度为ρ铅=11g/cm3。(取水的密度ρ水=1.0×103kg/m3,g=10N/kg)
(1)有经验的钓鱼者会使浮标体积的三分之一露出水面,此时浮标受到的浮力是多大?
(2)小明看见爸爸有一种体积为0.5cm3的铅坠,这种铅坠受到的重力为多少?
(3)如果使用这种铅坠,浮标静止时浸入水中的体积是多大?(设:铅坠末接触池底,浮标的质量、钓线、鱼钩、鱼饵的体积及质量均不计)
4.疫情期间,全国很多地方实行疫区封闭管理,使用无人机进行常态化安全巡查,如图所示。无人机起飞前,放在地面上要确保脚架平稳着地;启动后,利用遥控器可控制它运动和工作。该无人机的部分参数如下表。
机身尺寸(毫米) 400×300×200
机身质量(千克) 25
飞机着地总面积(厘米2) 10
最大载物量(千克) 10
(1)无人机利用携带的焦距一定的微型摄像机进行航拍,来自地面景物的光通过摄像机镜头,会聚在感光晶片上,形成倒立、 (选填“放大”或“缩小”)的实像;当无人机下降时,须 (选填“增大”或“减小”)镜头与感光晶片间的距离,才能拍摄到清晰的画面。
(2)无人机匀速降落过程中,其所受重力G和升力F的大小关系为 。
(3)该无人机空载停放在地面上时,对地面产生的压强为多少?(写出计算过程)
5.跳水馆池水深度要适当,水过浅会发生危险,水过深则造成浪费。某科研小组想研究某高度跳台水池中水的合理深度,用仿真人体模型进行“模拟跳水”测试,将人体模型从距水面6米处静止释放,观察其触底情况。已知该人体模型重600牛,体积为0.059m3。(不考虑空气阻力)
(1)仿真人体模型入水后会受到浮力,其最大值是 590 牛。
(2)由于人体模型入水后受到的浮力与其重力大小相当,粗略测算时视为抵消,若剩下的平均阻力为其重力的1.5倍,则本次测试中池水至少多深才能保证人体模型不触池底?
(3)图甲是跳水运动员入水前的示意图,t1是人起跳的瞬间,t2为腾空至最高点的瞬间,t3是即将入水的瞬间。图乙要描述t1~t3之间速度变化的大致图像,请结合所学知识将其补充完整。
6.在北京冬奥会上,中国运动员苏翊鸣勇夺单板滑雪大跳台金牌。
(1)滑雪板底面越宽大,对雪地的压强 。
(2)若滑雪板与雪地总接触面积为0.4米2,苏翊鸣和滑雪板的总质量为72千克,当他穿着滑雪板站立在水平雪地上时,对雪地的压强为多大?
(3)图甲是他在决赛中的完美飞行轨迹,AB是飞跃跳台的上升阶段,BC是下落阶段。请在图乙中画出他在飞行过程中速度随时间变化的大致曲线图。(v0为A点的速度,不计空气阻力)
7.图甲为某自动注水装置的部分结构模型简图,底面积为200cm2的柱形水箱内装有质量为5kg的水,竖直硬细杆上端通过力传感器固定,下端与不吸水的实心长方体A连接(物体A的高度为0.2m)。打开水龙头,水箱中的水缓慢排出,细杆对力传感器作用力F的大小随排出水的质量m变化的关系如图乙所示,当排出水的质量达到4kg时,A刚好全部露出水面,由传感器控制开关开始注水。不计细杆重力,水的密度为1.0×103kg/m3。
(1)开始注水时,水箱内的水受到的重力是 10 N;
(2)从开始放水到物体A上表面刚好与液面相平时,水箱底部受到水的压强变化量是
Pa;
(3)请通过推理计算物体A的密度(写出必要的文字说明、表达式及最后结果)。
8.善于奇思妙想的小强及其兴趣小组在实验室(温度为20℃)进行综合实验。
(1)该小组想研究“密度计的工作原理”。图甲所示是密度计的简化模型,在一根粗细均匀的玻璃管内放一些小铅粒使其能竖直漂浮在液体中,设玻璃管浸入液体的深度为h液,该液体密度为ρ液,密度计漂浮在水中时浸入水中的深度为h水,水的密度为ρ水,则浸入液体的深度h液=________(用给出的物理量表示)。
(2)该小组想继续探究“某液体的密度和温度的关系”,设计了如图乙所示装置,长为0.6m的绝缘轻质杠杆ab悬挂在高处,可绕O点转动。杠杆a端的轻质细线悬挂一体积为1×10﹣3m3的实心合金块,浸没在烧杯内的液体中。b端轻质细线悬挂的铜柱在上下移动时能带动滑片P移动。滑片P重力和摩擦不计。
①若电源电压为3V,滑动变阻器标有“100Ω 1A”字样。在电路中串联一个量程为0~15mA的电流表,为保证电路安全,定值电阻R的最小阻值是________Ω。
②小强在给该液体加热过程中发现,电流表示数减小,则可得出该液体的密度随温度升高而________(选填“增大”、“减小”或“不变”)(除烧杯内的液体外,装置中其他物体的热胀冷缩忽略不计,合金块始终浸没)。
(3)该小组还想利用此装置继续测量该合金块的密度。已知该烧杯中液体在温度为20℃时计的密度为1.1×103kg/m3。杠杆水平平衡时,铜柱质量为2kg,点O距杠杆b端0.2m。则的密度是________kg/m3(g取10N/kg)
9.一个底面积为10m2的圆柱状容器,装有适量的水,现在将一个体积为20m3、密度为0.8×103kg/m3的物体A放入其中,最终物体A漂浮于水面上。
则:
(1)物体A所受到的浮力是多少?
(2)如图所示,若将画斜线部分截取下来并取出(其体积为浸入水中体积的一半),则取出的那部分物体的质量是多少?
(3)待剩余部分再次静止后,容器底部受到压强减小了多少?(g=10N/kg)
10.一个圆柱形容器放在水平桌面上,在容器中放着一个密度小于水的均匀圆柱体M,且圆柱体M通过细线与圆柱形容器底部相连,如图甲所示(细线未画出)。现慢慢向容器中加水,圆柱形容器内水面高度为h,如图乙所示。测得水面高度h与所加水的质量m的关系如图丙所示。所加水量在3kg以内的过程中无水溢出。(图甲图乙中圆柱体和容器大小,以及细绳的长度不具有暗示意义)求:
(1)由甲图可知圆柱体M刚好漂浮时容器中水的深度h=8cm,请回答圆柱体M的高度H=________ cm。
(2)圆柱体M的密度;
(3)圆柱体M的的重力;
11.如图甲,水平升降台上有一圆柱形容器,容器中装有一定量的水,现将一实心正方体M(不吸水)悬挂在不可伸缩的细绳下端(细绳体积忽略不计),使M浸没水中并刚好与容器底接触但不产生压力,现使升降台匀速下降,图乙是绳的拉力F随时间t的变化图象。
(1)在t1和 t2时刻,M所受浮力分别为F浮1、F浮2,则 F浮1________F浮2(选填“>”、“<”或“=”)。
(2)求物体M的密度。
(3)当绳子的拉力为0.63N时,正方体上表面到水面的距离。
答案及解析
1.解:(1)浮冰的重力:
G冰=mg=51×103kg×10N/kg=5.1×105N;
由于浮冰漂浮:
则:F浮=G冰=5.1×105N;
(2)根据阿基米德原理可知,浮冰在海面以下的体积V排50m3;
(3)因为浮冰漂浮于海面上,
所以F浮=ρ海水gV排=G冰,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
又因为冰熔化成水后,其质量不变,重力不变,
所以G水=ρ水gV水=G冰,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
由①②可得:ρ海水gV排=ρ水gV水,
所以V排<V水,
即:浮冰熔化为水的体积大于浮冰排开水的体积。
所以浮冰全部熔化后,海平面水位上升;
(4)绿色出行。
答:(1)浮冰受到的浮力是5.1×105N;
(2)浮冰在海面以下的体积是50m3;
(3)如果海面所有浮冰全部熔化后,海平面水位上升;
(4)绿色出行。
2.解:(1)塑料块处于漂浮状态,所以所受浮力为:F浮1=GA=mAg=0.4kg×10N/kg=4N;
(2)图乙塑料块A上口边缘与水面相平,V排=VA=5×10﹣3m3,此时A受到的浮力为:F浮2=ρ水V排g=1.0×103kg/m3×5×10﹣3m3×10N/kg=50N;
图乙中物体的受力关系为:F浮2=GA+GB,
所以石块B的重力为:GB=F浮2﹣GA=50N﹣4N=46N。
答:(1)塑料块受到的浮力为4N;
(2)石块B的重力为46N。
3.解:(1)浮标有的体积露出水中时:
则浮标浸入水中的体积:V排V浮标15cm3=10cm3;
此时浮标受到的浮力为F浮=ρ水gV排=1.0×103 kg/m3×10N/kg×10×10﹣6m3=0.1N;
(2)这种铅坠质量为m=ρV=11g/cm3×0.5cm3=5.5g=5.5×10﹣3kg;
受到的重力为G=mg=5.5×10﹣3kg×10N/kg=0.055N;
(3)由于铅坠未接触池底,浮标和铅坠静止时受到的浮力:
F浮′=G总=0.055N,
根据F浮=ρ水gV排可得,此时排开水的体积:
V排′5.5×10﹣6m3=5.5cm3;
浮标浸入水中的体积
V浸=V排′﹣V=5.5cm3﹣0.5cm3=5cm3;
答:(1)此时浮标受到的浮力是0.1N;
(2)这种铅坠受到的重力为0.055N;
(3)浮标静止时浸入水中的体积为5cm3。
4.解:(1)摄像机的镜头相当于一个凸透镜,其成像的原理是:当物距大于二倍焦距时,凸透镜成倒立缩小的实像;
当无人机下降时,物距减小,像距变大,需增大镜头与感光晶片的距离,才能拍摄到清晰的画面;
(2)无人机匀速降落过程中,无人机处于平衡运动状态,螺旋桨产生的升力等于重力;
(3)无人机空载停放在地面上时对水平面的压力为:
F压=G=mg=25kg×10N/kg=250N,
对地面产生的压强为:
p2.5×105Pa。
故答案为:(1)缩小;增大;(2)重力G等于升力F;(3)该无人机空载停放在地面上时,对地面产生的压强为2.5×106Pa。
5.解:(1)由浮力公式F浮=ρ水gV排可得浮力的最大值是:
F浮=ρ水gV排=ρ水gV=1.0×103kg/m3×10N/kg×0.059m3=590N;
(2)由机械能守恒定律知,动能的大小就是重力势能的减小量,入水后,依据题意,人体模型受到的浮力与其重力大小相当,视为抵消,仅受向上的阻力为1.5mg,
由动能定理可得:mgh=1.5mgdmin,
可得池水深度至少是:dmin4m;
(3)t2~t3期间,运动员做自由落体运动,因为运动员仅受重力,故合外力不变,加速度不变,故斜率不变。如图所示:
故答案为:(1)590;(2)本次测试中池水至少4m深才能保证人体模型不触池底;(3)见解答图。
6.解:(1)压强的大小与压力大小和受力面积大小有关,所以滑雪板底面越宽大,在压力相同的情况下,由于受力面积越大,所以 滑雪板对雪地的压强越小;
(2)苏翊鸣和滑雪板的总重力:G=mg=72kg×10N/kg=720N;
当他穿着滑雪板站立在水平雪地上时,对雪地的压力F=G=720N;
对雪地的压强:p1800Pa;
(3)他在飞行过程中,上升阶段:动能转化为重力势能,动能减小,速度减小;下落阶段:重力势能转化为动能,动能增大,速度增大;
所以他在整个过程中的速度先变小,当上升到最高点B时,速度最小,接着下落过程速度变大;
速度随时间变化的大致曲线图如图所示:
答:(1)越小;
(2)当他穿着滑雪板站立在水平雪地上时,对雪地的压强为1800Pa;
(3)图见解析。
7.解:(1)水箱内剩余水的重力为:G剩=m剩g=(5kg﹣4kg)×10N/kg=10N;
(2)根据题意和图像可知,从开始放水到物体A上表面刚好与液面相平时,放出水的质量为1kg,
该过程中物体A始终浸没在水中,则物体A受到的浮力大小不变,
又因为水对水箱底部的压力:F=G水+F浮,
所以,该过程中水对水箱底部的压力变化量为:ΔF=ΔG水=G排水=m排水g=1kg×10N/kg=10N,
则水箱底部受到水的压强变化量为:Δp500Pa。
(3)由图乙可知,在排水量为0~1kg范围内,F不变,A受到细杆对它竖直向下的压力和重力以及竖直向上的浮力作用且F浮=F+G,A处于浸没状态,即VA=V排,排水前A上表面上方水的质量为1kg;
在F从零增大到2N的范围内,A受到竖直向下的重力和竖直向上的浮力、细杆对A竖直向上的拉力的作用,
且G=F+F浮,在排水量为4kg时,A受到的浮力为零,即GA=F拉=2N;
当A完全浸没时受到的浮力为:F浮=GA+F压=2N+8N=10N,
A的体积为:VA=V排10 3m3,
A的密度为:ρA0.2×103kg/m3;
故答案为:(1)10;
(2)500;
(3)物体A的密度为0.2×103kg/m3,推理过程见解析。
8.(1)ρ水h水/ρ液
(2)200;减小
(3)2.1x103
【解析】(1)密度计始终在液面漂浮,根据浮沉条件可知,它在水中受到的浮力和在液体中受到的浮力相等,据此列出等式,并用阿基米德原理将等式拆开,带入数据计算即可;
(2)①为了保证电流表的安全,当变阻器的阻值为零时,电流也不能超过量程,根据计算定值电阻的最小阻值;
②首先根据电流表的示数变化分析变阻器阻值的变化,进而推断出滑片的移动方向,再确定杠杆的旋转方向,接下来根据杠杆的旋转方向确定a端物体受到浮力的变化,最后根据阿基米德原理确定液体密度的变化。
(3)首先根据杠杆的平衡条件计算出a端合金块受到的拉力,然后根据G=F浮+F拉列出等式,用密度公式和阿基米德原理将等式拆开,最后推导计算合金块的密度即可。
【解答】(1)密度计始终漂浮在液面上,
那么F浮水=F浮液;
ρ水gV排水=ρ液gV排液
ρ水V排水=ρ液V排液
ρ水Sh水=ρ液Sh液;
ρ水h水=ρ液h液;
解得:;
(2)①定值电阻的最小阻值为:。
②电流表的示数变小,那么变阻器的阻值增大,即铜柱向上移动,则左端合金块下沉,说明合金块受到的拉力增大了。根据G=F浮+F拉可知,合金块受到的浮力减小了。根据阿基米德原理F浮=ρ液gV排可知,合金块的V排不变,那么液体密度变小了。因此液体的密度随温度升高而减小。
(3)根据杠杆的平衡条件得到:G铜×OB=F拉×OA;
2kg×10N/kg×0.2m=F拉×(0.6m-0.2m);
解得:F拉=10N;
根据二力平衡的知识得到:G=F浮+F拉;
ρgV=ρ液gV+10N;
ρ×10N/kg× 1×10﹣3m3 = 1.1×103kg/m3 ×10N/kg× 1×10﹣3m3+10N;
解得:ρ= 2.1x103 kg/m3 。
9.(1)由题意可知:物体A的密度ρA=0.8×103kg/m3,体积VA=20m3,质量mA=ρAVA=0.8×103kg/m3×20m3=1.6×104kg,则GA=mAg=1.6×104kg×10N/kg=1.6×105N.
∵物体A漂浮于水面上,∴物体A所受的浮力F浮=GA=1.6×105N
(2)由F浮=ρ水gV排得:
取出的那部分物体的体积V′= V排= ×16m3=8m3,质量为m′=ρAV′=0.8×103kg/m3×8m3=6.4×103kg。根据取出的那部分物体的重力G′=m′g=6.4×103kg×10N/kg=6.4×104N.S=10m2,则压力的改变量△F=G′=6.4×104N
(3)容器底部受到压强减小了
【解析】1、根据浮沉条件,物体A的密度小于水的密度,所以物体A在水中处于漂浮状态,浮力等于物体A的重力。由物体的密度和体积求出物体的质量,再根据公式G=mg;
2、根据浮力公式变形得可以求出浸在水中的物体A的体积,可求出1/2体积的大小,再由可求出截取部分物体的质量;
3、截取部分漂浮的物体后,液体对容器底部的压力减小了,减小的这部分压力数值上等于截取部分物体的重力,根据压力的减小值可以计算出压强的减小值。
10.(1)10
(2)当圆柱体飘浮时:F浮=G
ρ水gSh高=ρ物gSH 1000kg/m3×gS×0.08m=×ρ物gS×0.1m
得ρ物=800kg/m3
(3)由图得,当容器内水的深度从8cm到12cm时,
水的体积增加量:△V=△m/ρ水=1kg/1000kg/m3=0.001m3
在这个过程中,圆柱体一直处于漂浮状态,即S容=△V/△h=0.001m3/0.04m=0.025m2
由图得,当容器内水的深度从0cm到8cm时,
水的体积增加量:△V’=△m’/ρ水=0.8kg/1000kg/m3=0.0008m3
在圆柱体漂浮前,S容-S圆=△V’/△h’=0.0008m3/0.08m=0.01m2
即S圆=0.015m2
G=ρ物gS圆H=800kg/m3×10N/kg×0.015m2×0.08m=12N
【解析】在开始的一段时间内,M受到的浮力小于重力,它在容器底部静止不动,此时由于它占有部分体积,所以水面高度上升的较快;当水面高度达到8cm时,M受到的浮力等于重力,它开始在水面漂浮,随着水面的上升而上升;当水面高度达到12cm时,下面的细线被拉直,M不再上升;当水面高度达到14cm时,M被完全淹没,此后水面不断上升,而M的位置则保持不变;
(1)从图中找到木块刚好漂浮时水面的高度,以及细线被拉直时到M完全淹没时的水面高度变化,然后二者相加就是M的高度H;
(2)当M刚好漂浮时,水面的高度为8cm,根据漂浮条件列出浮力和重力的关系式,用阿基米德原理和密度公式将二者分解计算即可;
(3) 根据图甲可知,当容器内水的深度从8cm到12cm时, M处于漂浮状态,跟随水面不断上升。确定此段时间内加入水的质量,然后根据密度公式计算出加入水的体积V水,再根据计算出容器的底面积。
当容器内水的深度从0cm到8cm时, M在容器底部保持不动。根据图片确定这段时间内加入水的质量 △m ',根据密度公式计算出加入水的体积 △V ',再根据△S'= △V'/△h’计算出容器的底面积和M的底面积之差,接下来根据 S容-S圆= △S'计算出M的底面积,最后根据公式 G=m物g=ρ物gS圆H计算即可。
【解答】(1)根据图甲可知,木块刚好漂浮时水面的高度8cm,细线被拉直时到M完全淹没时的水面高度变化:14cm-12cm=2cm,那么圆柱体M的高度为:H=8cm+2cm=10cm。
(2)当圆柱体飘浮时,浮力等于重力,
即F浮=G;ρ水gSh高=ρ物gSH ;
1000kg/m3×gS×0.08m=×ρ物gS×0.1m;
解得:ρ物=800kg/m3。
(3)由图得,当容器内水的深度从8cm到12cm时,
水的体积增加量:△V=△m/ρ水=1kg/1000kg/m3=0.001m3;
在这个过程中,圆柱体一直处于漂浮状态,即S容=△V/△h=0.001m3/0.04m=0.025m2;
由图得,当容器内水的深度从0cm到8cm时,
水的体积增加量:△V’=△m’/ρ水=0.8kg/1000kg/m3=0.0008m3;
在圆柱体漂浮前,加入水的底面积△S'=△V’/△h’=0.0008m3/0.08m=0.01m2;
因为S容-S圆=△S';
那么S圆=S容-△S'=0.025m2-0.01m2=0.015m2;
圆柱体M的重力:G=m物g=ρ物gS圆H=800kg/m3×10N/kg×0.015m2×0.08m=12N。
11.(1)>
(2)G=0.81N
m= ==0.081kg
F浮=G-F拉=0.81N-0.54N=0.27N
∵浸没
∴V排=V物
∴F浮=ρ液gV排=ρ液gV物
V物= ==2.7x10-5m3
ρ===3×103kg/m3
(3)F浮'=G-F拉=0.81N-0.63N=0.18N
=2:3
设正方体边长为a,
上表面距离水面高度为h
V物=2.7x10-5m3=a3
a=0.03m
h= ·h=0.01m
【解析】根据乙图可知,在物体露出水面前,它排开水的体积等于自身体积,因此浮力保持不变,根据F=G-F浮可知,绳子的拉力保持不变;从开始露出水面到完全露出水面的过程中,物体排开水的体积不断减小,浮力不断减小,那么绳子的拉力不断增大。当物体完全露出水面后,物体不受浮力,此时绳子的拉力等于物体的重力,保持不变。
(1)首先根据乙图确定两个时刻时物体M受到拉力的大小关系,然后根据F浮=G-F比较两个时刻时受到浮力的大小关系;
(2)根据乙图,确定物体的重力和完全浸没时绳子的拉力,根据 F浮=G-F拉 计算出浸没时受到的浮力,根据 计算物体的体积,最后根据计算物体的密度。
(3)首先根据 F浮’=G-F拉 计算出此时物体受到的浮力,然后根据浮力与V排成正比,计算出此时V排和物体完全浸没时体积的比值,进而得到露出水面的体积和物体体积的比值。因为物体为长方体,所以两个体积之比等于上表面到水面高度与正方体边长的比,最后带入正方体的边长计算即可。
【解答】(1)根据图乙可知,t1时刻的拉力小于t2时刻的拉力,根据F浮=G-F可知,t1时刻的浮力大于t2时刻的浮力,即F浮1>F浮2;
(2)根据乙图可知,当物体完全出水后拉力F=0.81N,
根据二力平衡的知识得到,物体M的重力G=F=0.81N;
那么物体M的质量为: ;
当物体M完全浸没时受到的拉力为0.54N,
那么此时受到的浮力F浮=G-F拉=0.81N-0.54N=0.27N;
∵因为物体完全浸没在水中,
∴所以排开水的体积等于物体的体积,即V排=V物;
根据阿基米德原理F浮=ρ液gV排=ρ液gV物得到:
物体的体积;
物体的密度=。
(3)当绳子的拉力为0.63N时受到的浮力 F浮'=G-F拉=0.81N-0.63N=0.18N;
根据阿基米德原理F浮=ρ液gV排可知,当液体密度相同时,浮力与V排成正比,得到:
;
因为V物=V排'+V露,
那么:;
设正方体边长为a,上表面距离水面高度为h,
那么正方体上表面到水面的距离与物体的边长之比:;
根据V物=2.7x10-5m3=a3得到:
物体M的边长a=0.03m;
那正方体上表面到水面的距离。
浮力、压强的计算
同课章节目录
