18.2.3 正方形 课后练习(含答案)
文档属性
| 名称 | 18.2.3 正方形 课后练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 580.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 09:23:54 | ||
图片预览



文档简介
18.2.3正方形
一、单选题
1.下列四个命题正确的是( )
A.菱形的对角线相等
B.一组对边相等,另一组对边平行的四边形是平行四边形
C.对角线相等的平行四边形是矩形
D.对角线互相垂直的平行四边形是正方形
2.矩形,菱形,正方形都具有的性质是( )
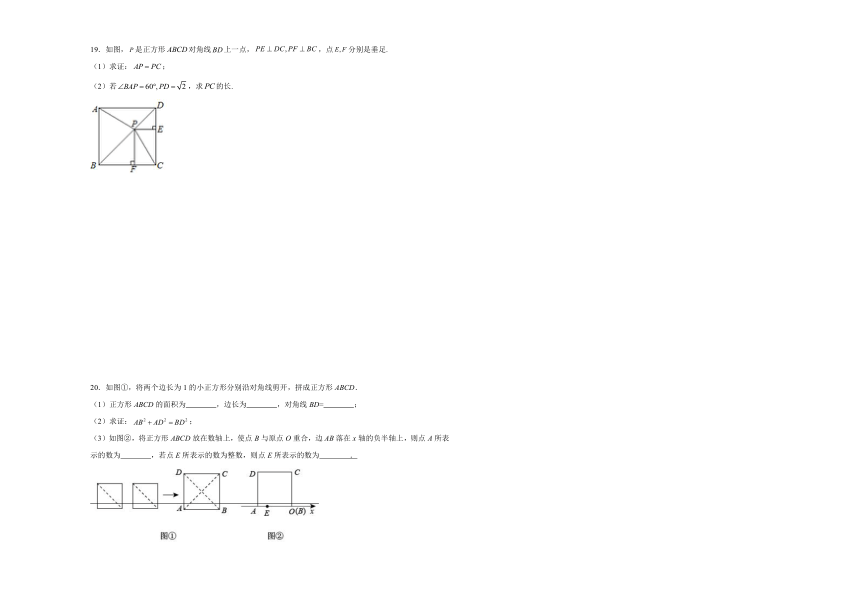
A.对角线相等 B.对角线互相平分
C.对角线平分组对角 D.四个角都是直角
3.在一个四边形ABCD中依次连接各边的中点得到的四边形是矩形,则对角线AC与BD需要满足的条件是( )
A.垂直 B.相等
C.垂直且相等 D.不再需要条件
4.下列判定正确的是( )
A.对角线互相垂直的四边形是菱形
B.两条对角线相等且互相垂直的四边形是正方形
C.四边相等且有一个角是直角的四边形是正方形
D.一组对边平行,一组对边相等的四边形是平行四边形
5.正方形的面积是4cm2,那么对角线是( )cm.
A.2cm B.4cm C.cm D.cm
6.如图,将正方形纸片折叠,使边、均落在对角线上,折痕为、,点在上,点在上,则的大小为( )
A.15° B.30° C.45° D.60°
7.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则两对角线OC,BD的交点的坐标是( )
A.(6,3) B.(6,3) C.(3,3) D.(6,6)
8.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.4 C.8 D.16
9.如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( )
A.6cm2 B.36cm2 C.18cm2 D.2cm2
10.如图,在边长为4的正方形中,点E、F分别是边上的动点,且,连接,则的最小值为( )
A.8 B. C. D.
二、填空题
11.若正方形的对角线的长为4,则该正方形的面积为_________.
12.已知正方形的一条对角线长是,则它的面积等于__________.
13.如图,矩形ABCD的对角线相交于点O,请添加一个条件______________(只需添加一个即可),使矩形ABCD是正方形.
14.如图,在四边形中,于点,点,,,分别为边,,,的中点,顺次连接,,,,则四边形是______.
15.如图,A、B、C、D都是格点(小正方形的顶点),动点E在线段AC上,若点A的坐标是(1,1),则当△ADE与△ABC相似时,动点E的坐标是_____.
三、解答题
16.如图,在正方形中,对角线与相交于点O,图中有多少个等腰三角形?
17.如图,正方形ABCD的边长为4,连接对角线AC,点E为BC边上一点,将线段AE绕点A逆时针旋转45°得到线段AF,点E的对应点F恰好落在边CD上,过F作FM⊥AC于点M.
(1)求证:BE=FM;
(2)求BE的长度.
18.图1,图2,图3,图4都是的正方形网格,每个小正方形的顶点称为格点.每个小正方形的边长均为1.在图1,图2,图3中已画出线段,在图4中已画出点,按下列要求画图.
(1)在图1中,以格点为顶点,为一边画一个等腰三角形;
(2)在图2中,以格点为顶点,为一边画一个平行四边形;
(3)在图3中,以格点为顶点,为一边画一个正方形;
(4)在图4中,以点为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
19.如图,是正方形对角线上一点,,点分别是垂足.
(1)求证:;
(2)若,求的长.
20.如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .
参考答案
1.C
2.B
3.A
4.C
5.C
6.C
7.C
8.B
9.B
10.D
11.8
12.16
13.AB=AD,答案不唯一
14.矩形
15.(3,3)或(,).
16.以正方形的对角线为斜边的等腰三角形共有4个,分别是△ABC,△ADC,△ABD,△BCD,
以正方形的边为斜边的等腰三角形共有4个,分别是△AOB,△BOC,△OCD,△AOD,
故总共有8个等腰三角形,且都是等腰直角三角形.
17.(1)证明:在正方形ABCD中,线段AE绕点A逆时针旋转45°得到线段AF
∠CAB=45°,∠EAF=45°,AE=AF
∠FAM=∠EAB
∵FM⊥AC
∠FMA=∠B=90°
≌(AAS)
BE=FM
(2)在正方形ABCD中,边长为4
AC=,∠DCA=45°
≌
∴AM=AB=4
MC=AC—AM=—4
∵是等腰直角三角形
BE=MF=MC=—4
18.解:(1)如图,符合条件的C点有5个:
;
(2)如图共有三类符合条件的CD共有9条,每类情况CD向右平移1个单位如第4个图,平移2个单位如第5个图,平行四边形ABCD共有九个
(3)如图,利用旋转作图,以A点为圆心,AB=为半径顺时针旋转90°得AD,在以B为圆心,AB长为半径逆时针旋转90°,得BC,连结CD,则四边形ABCD为正方形,正方形ABCD即为满足条件的图形:
(4)如图③,边长为的正方形ABCD的面积最大.
.
此时正方形的面积为()2=10.
19.(1)证明:
∵四边形是正方形,为对角线,
∴,
在和中
,
∴,
∴.
(2)解:由(1)知,
∴,
∴,
∵四边形是正方形,是对角线,
∴,
∵,
∴,
∵,
∴,
∴.
20.解:(1)由图形拼接不改变面积可得:正方形ABCD=
由边长是面积的算术平方根可得:正方形ABCD的边长为
由拼接可得
大正方形的面积
(负根舍去)
故答案为:2,,2;
(2)小正方形的面积
由拼接可得:
大正方形的面积,
(3)由(1)知:在数轴负半轴上,
点表示
在之间且表示整数,
表示
故答案为:,.
一、单选题
1.下列四个命题正确的是( )
A.菱形的对角线相等
B.一组对边相等,另一组对边平行的四边形是平行四边形
C.对角线相等的平行四边形是矩形
D.对角线互相垂直的平行四边形是正方形
2.矩形,菱形,正方形都具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线平分组对角 D.四个角都是直角
3.在一个四边形ABCD中依次连接各边的中点得到的四边形是矩形,则对角线AC与BD需要满足的条件是( )
A.垂直 B.相等
C.垂直且相等 D.不再需要条件
4.下列判定正确的是( )
A.对角线互相垂直的四边形是菱形
B.两条对角线相等且互相垂直的四边形是正方形
C.四边相等且有一个角是直角的四边形是正方形
D.一组对边平行,一组对边相等的四边形是平行四边形
5.正方形的面积是4cm2,那么对角线是( )cm.
A.2cm B.4cm C.cm D.cm
6.如图,将正方形纸片折叠,使边、均落在对角线上,折痕为、,点在上,点在上,则的大小为( )
A.15° B.30° C.45° D.60°
7.如图,四边形OBCD是正方形,O,D两点的坐标分别是(0,0),(0,6),点C在第一象限,则两对角线OC,BD的交点的坐标是( )
A.(6,3) B.(6,3) C.(3,3) D.(6,6)
8.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.2 B.4 C.8 D.16
9.如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( )
A.6cm2 B.36cm2 C.18cm2 D.2cm2
10.如图,在边长为4的正方形中,点E、F分别是边上的动点,且,连接,则的最小值为( )
A.8 B. C. D.
二、填空题
11.若正方形的对角线的长为4,则该正方形的面积为_________.
12.已知正方形的一条对角线长是,则它的面积等于__________.
13.如图,矩形ABCD的对角线相交于点O,请添加一个条件______________(只需添加一个即可),使矩形ABCD是正方形.
14.如图,在四边形中,于点,点,,,分别为边,,,的中点,顺次连接,,,,则四边形是______.
15.如图,A、B、C、D都是格点(小正方形的顶点),动点E在线段AC上,若点A的坐标是(1,1),则当△ADE与△ABC相似时,动点E的坐标是_____.
三、解答题
16.如图,在正方形中,对角线与相交于点O,图中有多少个等腰三角形?
17.如图,正方形ABCD的边长为4,连接对角线AC,点E为BC边上一点,将线段AE绕点A逆时针旋转45°得到线段AF,点E的对应点F恰好落在边CD上,过F作FM⊥AC于点M.
(1)求证:BE=FM;
(2)求BE的长度.
18.图1,图2,图3,图4都是的正方形网格,每个小正方形的顶点称为格点.每个小正方形的边长均为1.在图1,图2,图3中已画出线段,在图4中已画出点,按下列要求画图.
(1)在图1中,以格点为顶点,为一边画一个等腰三角形;
(2)在图2中,以格点为顶点,为一边画一个平行四边形;
(3)在图3中,以格点为顶点,为一边画一个正方形;
(4)在图4中,以点为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
19.如图,是正方形对角线上一点,,点分别是垂足.
(1)求证:;
(2)若,求的长.
20.如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:;
(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .
参考答案
1.C
2.B
3.A
4.C
5.C
6.C
7.C
8.B
9.B
10.D
11.8
12.16
13.AB=AD,答案不唯一
14.矩形
15.(3,3)或(,).
16.以正方形的对角线为斜边的等腰三角形共有4个,分别是△ABC,△ADC,△ABD,△BCD,
以正方形的边为斜边的等腰三角形共有4个,分别是△AOB,△BOC,△OCD,△AOD,
故总共有8个等腰三角形,且都是等腰直角三角形.
17.(1)证明:在正方形ABCD中,线段AE绕点A逆时针旋转45°得到线段AF
∠CAB=45°,∠EAF=45°,AE=AF
∠FAM=∠EAB
∵FM⊥AC
∠FMA=∠B=90°
≌(AAS)
BE=FM
(2)在正方形ABCD中,边长为4
AC=,∠DCA=45°
≌
∴AM=AB=4
MC=AC—AM=—4
∵是等腰直角三角形
BE=MF=MC=—4
18.解:(1)如图,符合条件的C点有5个:
;
(2)如图共有三类符合条件的CD共有9条,每类情况CD向右平移1个单位如第4个图,平移2个单位如第5个图,平行四边形ABCD共有九个
(3)如图,利用旋转作图,以A点为圆心,AB=为半径顺时针旋转90°得AD,在以B为圆心,AB长为半径逆时针旋转90°,得BC,连结CD,则四边形ABCD为正方形,正方形ABCD即为满足条件的图形:
(4)如图③,边长为的正方形ABCD的面积最大.
.
此时正方形的面积为()2=10.
19.(1)证明:
∵四边形是正方形,为对角线,
∴,
在和中
,
∴,
∴.
(2)解:由(1)知,
∴,
∴,
∵四边形是正方形,是对角线,
∴,
∵,
∴,
∵,
∴,
∴.
20.解:(1)由图形拼接不改变面积可得:正方形ABCD=
由边长是面积的算术平方根可得:正方形ABCD的边长为
由拼接可得
大正方形的面积
(负根舍去)
故答案为:2,,2;
(2)小正方形的面积
由拼接可得:
大正方形的面积,
(3)由(1)知:在数轴负半轴上,
点表示
在之间且表示整数,
表示
故答案为:,.
