2.2气体实验定律(Ⅱ) 课件 (共25张PPT) 高二下学期物理粤教版(2019)选择性必修第三册
文档属性
| 名称 | 2.2气体实验定律(Ⅱ) 课件 (共25张PPT) 高二下学期物理粤教版(2019)选择性必修第三册 |  | |
| 格式 | pptx | ||
| 文件大小 | 775.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-06 21:09:51 | ||
图片预览






文档简介
(共25张PPT)
第二节
气体实验定律(Ⅱ)
学习目标
1.通过实验认识一定质量的气体在等容条件下其压强与温度之间的关系,及在等压条件下其体积与温度之间的关系。
2.掌握查理定律的内容、数学表达式;理解p-T图象的物理意义;
3.掌握盖-吕萨克定律的内容、数学表达式;理解V-T图象的物理意义。
4.会运用查理定律、盖—吕萨克定律解释生产生活中的一些现象,解决一些实际问题。
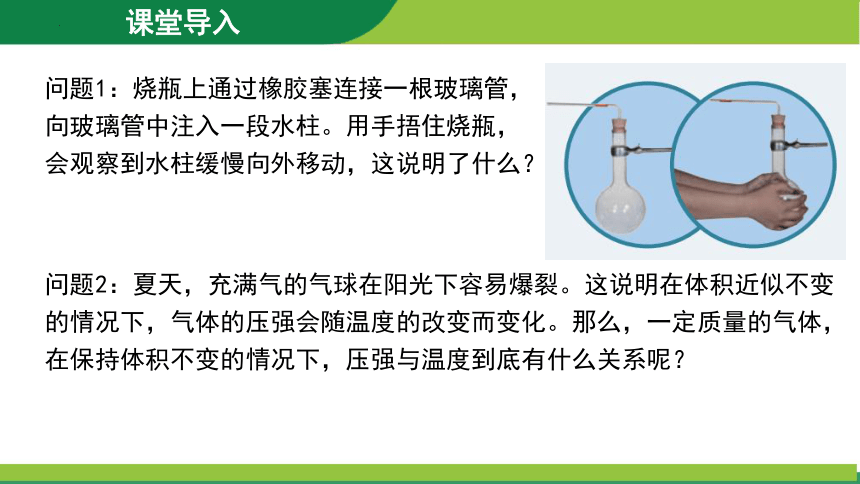
问题1:烧瓶上通过橡胶塞连接一根玻璃管,向玻璃管中注入一段水柱。用手捂住烧瓶,会观察到水柱缓慢向外移动,这说明了什么?
课堂导入
问题2:夏天,充满气的气球在阳光下容易爆裂。这说明在体积近似不变的情况下,气体的压强会随温度的改变而变化。那么,一定质量的气体,在保持体积不变的情况下,压强与温度到底有什么关系呢?
探究等容过程的规律
观察与思考:
如图所示是一个探究气体压强与温度变化关系的实验装置示意图,实验中,往细玻璃管内注入适量的红墨水,通过红墨水的移动观察气压的改变.把瓶先后放入盛着冰水混合物的容器和盛着热水的容器中,设法保持瓶内气体的体积不变,观察红墨水的移动情况,思考该过程气体压强和温度变化的关系。
大量实验证明,一定质量的气体,在体积保持不变的条件下,压强与热力学温度成正比。
等容变化——查理定律
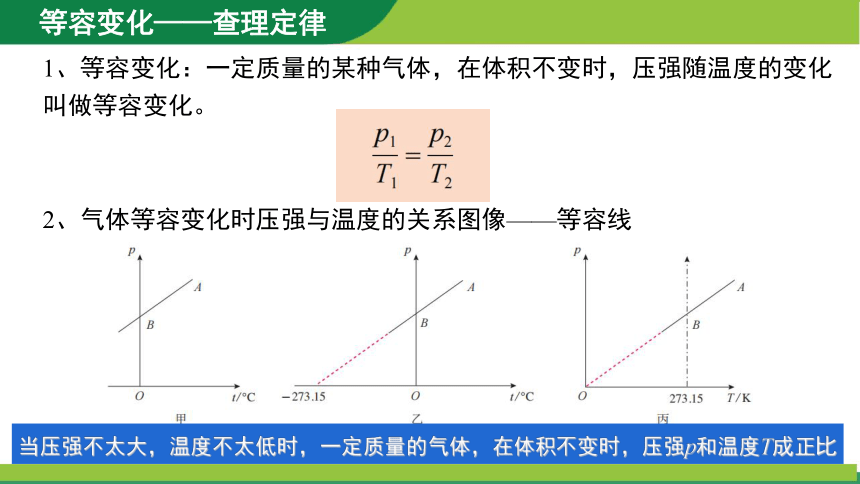
1、等容变化:一定质量的某种气体,在体积不变时,压强随温度的变化叫做等容变化。
2、气体等容变化时压强与温度的关系图像——等容线
当压强不太大,温度不太低时,一定质量的气体,在体积不变时,压强p和温度T成正比
等容变化——查理定律
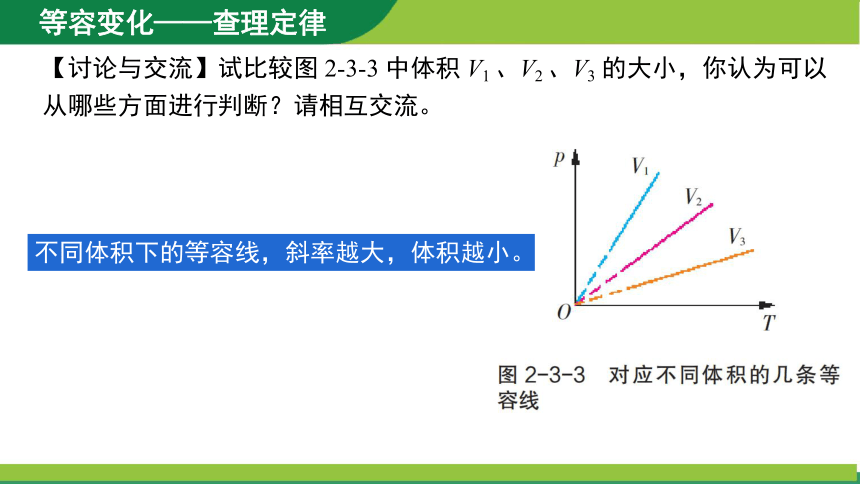
【讨论与交流】试比较图 2-3-3 中体积 V1 、V2 、V3 的大小,你认为可以从哪些方面进行判断?请相互交流。
不同体积下的等容线,斜率越大,体积越小。
查理定律的微观解释
一定质量的气体,体积保持不变,则单位体积中的分子数也保持不变。当温度升高时,分子热运动的平均动能增大,这使得单位时间内撞击到器壁单位面积上的分子数增多,同时也使得分子撞击器壁时对器壁的撞击力增大,从而使得气体的压强随之增大。这就是对气体等容变化规律的微观解释。
【例题1】某种气体的压强为 2×105 Pa,体积为 1 m3,温度为 200 K。它经过等温过程后体积变为 2 m3。随后,又经过等容过程,温度变为 300 K,求此时气体的压强。
等容变化——查理定律的应用
分析:封闭容器中的气体,在状态变化中气体质量不变。气体开始时的压强、体积和温度 p1、V1、T1,经过等温过程变为 p2、V2、T2,再经过等容过程变为 p2、V2、T2。我们可以分别运用玻意耳定律和查理定律求解 。
【例题1】某种气体的压强为 2×105 Pa,体积为 1 m3,温度为 200 K。它经过等温过程后体积变为 2 m3。随后,又经过等容过程,温度变为 300 K,求此时气体的压强。
等容变化——查理定律的应用
【例题2】案例1 某登山运动员在一次攀登珠穆朗玛峰的过程中,他手表的表面玻璃没有受到任何撞击,却突然爆裂了。
查阅该手表出厂时给出的参数为:27 ℃时表内气体压强为1 × 105 Pa,当内外压强差超过 6 × 104 Pa 时,手表表面玻璃可能爆裂。若已知当时气温是 -13 ℃,那么手表表面玻璃爆裂时表内气体压强为多大?外界大气压强为多大?
分析 手表的表壳与表面玻璃组合可以看成一个密闭容器,出厂时表壳内封闭着一定质量的空气,气压是一个大气压。手表出厂后随登山运动员上珠峰,可以认为表壳内的气体经历了一个等容过程(不考虑表壳的热胀冷缩)。根据查理定律可算出表壳内气体在山上的压强,结合表面玻璃爆裂条件,即可求出当时的外界大气压。
等容变化——查理定律的应用
等压变化与盖吕萨克定律
一定质量的气体,在压强不变的情况下,体积与温度有什么关系呢?
探究气体等压变化的关系
端开口的细玻璃管中,并将细玻璃管与温度计一起固定在刻度尺上,放入盛有水的烧杯,没入水中适当的深度,使封闭气体的温度和烧杯内水的温度相同,因此温度计的示数即可表示气体的温度。气体的体积(用气柱的长度表示)可由刻度尺直接读出。
(1)加热烧杯,待温度计示数稳定后,记下气体的温度和体积。
(2)按步骤(1)重复实验,记下几组对应的温度和体积值。
根据得到的数据,在压强不变的条件下,气体的温度与体积存在怎样的关系?是否与你的猜想相同?
等圧変化——盖吕萨克定律
1、大量实验证明,一定质量的气体,在压强保持不变的条件下,体积与热力学温度成正比。
2、等压变化:一定质量的某种气体,在压强不变时,体积随温度的变化叫做等压变化。
3、等压线:
想一想:你怎样判断图 2-3-5 中的压强 p1、p2、p3 的大小关系?
盖吕萨克定律的微观解释
一定质量的气体,当温度升高时,气体分子热运动的平均动能增大,这会使气体对器壁的压强增大。要使压强保持不变,必须减小气体分子的密集程度,使单位时间内与单位面积器壁碰撞的分子数减少,这在宏观上就表现为气体体积的增大。这就是对气体等压变化规律的微观解释。
查理定律与盖吕萨克定律的比较
气体实验定律
气体实验定律
玻意耳定律
查理定律
盖-吕萨克定律
压强不太大(相对大气压),温度不太低(相对室温)
这些定律的适用范围:
p1V1=p2V2
气体实验定律
【例题1】一定质量的理想气体,由状态A经状态B变为状态C,其中A到B过程为等压变化,B到C过程为等容变化。已知VA=0.3m ,TA=TC=300K,TB=400K。
(1)求气体在状态B时的体积大小;
(2)从微观的角度说明气体由状态A到C过程中压强如何变化。
分析
理想气体遵循气体实验定律。气体从状态A到B是等压变化,有pA=pB
气体实验定律
【例题2】如所示,固定的竖直气缸内有一个活塞,活塞的质量为 m,活塞横截面积为 S,气缸内封闭着一定质量的气体。现对缸内气体缓慢加热,并在活塞上缓慢加沙子,使活塞位置保持不变。忽略活塞与气缸壁之间的摩擦,已知气缸内气体的初始热力学温度为 T0,大气压强为 p0,重力加速度大小为 g。试求当所加沙子的质量为 M 时,气缸内气体的温度。
分析:
以气缸内的气体为研究对象。活塞位置保持不变,说明气缸内的气体为等容变化,遵循查理定律。气缸加热前气体的状态为初态,加热到热力学温度为 T 时的状态为末态。通过活塞受力平衡可分别求出气体初、末状态的气体压强。
气体实验定律
【迁移1】在上述例题中,已知最初缸内气体的高度为 h0。如果保持活塞上方所加的沙子不变,继续对气缸缓慢加热,活塞缓慢向上移动距离 h,此时气缸内气体温度是多少?
理想气体状态方程
以上我们研究气体状态的变化时,都只涉及两个物理量的变化。但在实际问题中,气体的压强、体积和温度这三个物理量往往是同时变化的。当这三个物理量同时变化时,又遵循什么规律呢?利用由实验得出的玻意耳定律和查理定律可推出这三个物理量的变化关系。
上式反映了一定质量的理想气体状态发生变化时,压强、体积和温度变化所遵循的规律,称为理想气体状态方程。式中 C 是常量,与气体的种类和质量有关。
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
第二节
气体实验定律(Ⅱ)
学习目标
1.通过实验认识一定质量的气体在等容条件下其压强与温度之间的关系,及在等压条件下其体积与温度之间的关系。
2.掌握查理定律的内容、数学表达式;理解p-T图象的物理意义;
3.掌握盖-吕萨克定律的内容、数学表达式;理解V-T图象的物理意义。
4.会运用查理定律、盖—吕萨克定律解释生产生活中的一些现象,解决一些实际问题。
问题1:烧瓶上通过橡胶塞连接一根玻璃管,向玻璃管中注入一段水柱。用手捂住烧瓶,会观察到水柱缓慢向外移动,这说明了什么?
课堂导入
问题2:夏天,充满气的气球在阳光下容易爆裂。这说明在体积近似不变的情况下,气体的压强会随温度的改变而变化。那么,一定质量的气体,在保持体积不变的情况下,压强与温度到底有什么关系呢?
探究等容过程的规律
观察与思考:
如图所示是一个探究气体压强与温度变化关系的实验装置示意图,实验中,往细玻璃管内注入适量的红墨水,通过红墨水的移动观察气压的改变.把瓶先后放入盛着冰水混合物的容器和盛着热水的容器中,设法保持瓶内气体的体积不变,观察红墨水的移动情况,思考该过程气体压强和温度变化的关系。
大量实验证明,一定质量的气体,在体积保持不变的条件下,压强与热力学温度成正比。
等容变化——查理定律
1、等容变化:一定质量的某种气体,在体积不变时,压强随温度的变化叫做等容变化。
2、气体等容变化时压强与温度的关系图像——等容线
当压强不太大,温度不太低时,一定质量的气体,在体积不变时,压强p和温度T成正比
等容变化——查理定律
【讨论与交流】试比较图 2-3-3 中体积 V1 、V2 、V3 的大小,你认为可以从哪些方面进行判断?请相互交流。
不同体积下的等容线,斜率越大,体积越小。
查理定律的微观解释
一定质量的气体,体积保持不变,则单位体积中的分子数也保持不变。当温度升高时,分子热运动的平均动能增大,这使得单位时间内撞击到器壁单位面积上的分子数增多,同时也使得分子撞击器壁时对器壁的撞击力增大,从而使得气体的压强随之增大。这就是对气体等容变化规律的微观解释。
【例题1】某种气体的压强为 2×105 Pa,体积为 1 m3,温度为 200 K。它经过等温过程后体积变为 2 m3。随后,又经过等容过程,温度变为 300 K,求此时气体的压强。
等容变化——查理定律的应用
分析:封闭容器中的气体,在状态变化中气体质量不变。气体开始时的压强、体积和温度 p1、V1、T1,经过等温过程变为 p2、V2、T2,再经过等容过程变为 p2、V2、T2。我们可以分别运用玻意耳定律和查理定律求解 。
【例题1】某种气体的压强为 2×105 Pa,体积为 1 m3,温度为 200 K。它经过等温过程后体积变为 2 m3。随后,又经过等容过程,温度变为 300 K,求此时气体的压强。
等容变化——查理定律的应用
【例题2】案例1 某登山运动员在一次攀登珠穆朗玛峰的过程中,他手表的表面玻璃没有受到任何撞击,却突然爆裂了。
查阅该手表出厂时给出的参数为:27 ℃时表内气体压强为1 × 105 Pa,当内外压强差超过 6 × 104 Pa 时,手表表面玻璃可能爆裂。若已知当时气温是 -13 ℃,那么手表表面玻璃爆裂时表内气体压强为多大?外界大气压强为多大?
分析 手表的表壳与表面玻璃组合可以看成一个密闭容器,出厂时表壳内封闭着一定质量的空气,气压是一个大气压。手表出厂后随登山运动员上珠峰,可以认为表壳内的气体经历了一个等容过程(不考虑表壳的热胀冷缩)。根据查理定律可算出表壳内气体在山上的压强,结合表面玻璃爆裂条件,即可求出当时的外界大气压。
等容变化——查理定律的应用
等压变化与盖吕萨克定律
一定质量的气体,在压强不变的情况下,体积与温度有什么关系呢?
探究气体等压变化的关系
端开口的细玻璃管中,并将细玻璃管与温度计一起固定在刻度尺上,放入盛有水的烧杯,没入水中适当的深度,使封闭气体的温度和烧杯内水的温度相同,因此温度计的示数即可表示气体的温度。气体的体积(用气柱的长度表示)可由刻度尺直接读出。
(1)加热烧杯,待温度计示数稳定后,记下气体的温度和体积。
(2)按步骤(1)重复实验,记下几组对应的温度和体积值。
根据得到的数据,在压强不变的条件下,气体的温度与体积存在怎样的关系?是否与你的猜想相同?
等圧変化——盖吕萨克定律
1、大量实验证明,一定质量的气体,在压强保持不变的条件下,体积与热力学温度成正比。
2、等压变化:一定质量的某种气体,在压强不变时,体积随温度的变化叫做等压变化。
3、等压线:
想一想:你怎样判断图 2-3-5 中的压强 p1、p2、p3 的大小关系?
盖吕萨克定律的微观解释
一定质量的气体,当温度升高时,气体分子热运动的平均动能增大,这会使气体对器壁的压强增大。要使压强保持不变,必须减小气体分子的密集程度,使单位时间内与单位面积器壁碰撞的分子数减少,这在宏观上就表现为气体体积的增大。这就是对气体等压变化规律的微观解释。
查理定律与盖吕萨克定律的比较
气体实验定律
气体实验定律
玻意耳定律
查理定律
盖-吕萨克定律
压强不太大(相对大气压),温度不太低(相对室温)
这些定律的适用范围:
p1V1=p2V2
气体实验定律
【例题1】一定质量的理想气体,由状态A经状态B变为状态C,其中A到B过程为等压变化,B到C过程为等容变化。已知VA=0.3m ,TA=TC=300K,TB=400K。
(1)求气体在状态B时的体积大小;
(2)从微观的角度说明气体由状态A到C过程中压强如何变化。
分析
理想气体遵循气体实验定律。气体从状态A到B是等压变化,有pA=pB
气体实验定律
【例题2】如所示,固定的竖直气缸内有一个活塞,活塞的质量为 m,活塞横截面积为 S,气缸内封闭着一定质量的气体。现对缸内气体缓慢加热,并在活塞上缓慢加沙子,使活塞位置保持不变。忽略活塞与气缸壁之间的摩擦,已知气缸内气体的初始热力学温度为 T0,大气压强为 p0,重力加速度大小为 g。试求当所加沙子的质量为 M 时,气缸内气体的温度。
分析:
以气缸内的气体为研究对象。活塞位置保持不变,说明气缸内的气体为等容变化,遵循查理定律。气缸加热前气体的状态为初态,加热到热力学温度为 T 时的状态为末态。通过活塞受力平衡可分别求出气体初、末状态的气体压强。
气体实验定律
【迁移1】在上述例题中,已知最初缸内气体的高度为 h0。如果保持活塞上方所加的沙子不变,继续对气缸缓慢加热,活塞缓慢向上移动距离 h,此时气缸内气体温度是多少?
理想气体状态方程
以上我们研究气体状态的变化时,都只涉及两个物理量的变化。但在实际问题中,气体的压强、体积和温度这三个物理量往往是同时变化的。当这三个物理量同时变化时,又遵循什么规律呢?利用由实验得出的玻意耳定律和查理定律可推出这三个物理量的变化关系。
上式反映了一定质量的理想气体状态发生变化时,压强、体积和温度变化所遵循的规律,称为理想气体状态方程。式中 C 是常量,与气体的种类和质量有关。
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
玻意耳定律
【例题4】一个足球的容积是2.5 L。用打气筒给这个足球打气,每打一次都把体积为125 mL、压强与大气压相同的气体打进足球内。如果在打气前足球就已经是球形并且里面的压强与大气压相同,打了20次后足球内部空气的压强是大气压的多少倍?你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
同课章节目录
- 第一章 分子动理论
- 第一节 物质是由大量分子组成的
- 第二节 分子热运动与分子力
- 第三节 气体分子运动的统计规律
- 第二章 气体、液体和固态
- 第一节 气体实验定律(Ⅰ)
- 第二节 气体实验定律(Ⅱ)
- 第三节 气体实验定律的微观解释
- 第四节 液体的表面张力
- 第五节 晶体
- 第六节 新材料
- 第三章 热力学定律
- 第一节 热力学第一定律
- 第二节 能量守恒定律及其应用
- 第三节 热力学第二定律
- 第四章 波粒二象性
- 第一节 光电效应
- 第二节 光电效应方程及其意义
- 第三节 光的波粒二象性
- 第四节 德布罗意波
- 第五节 不确定性关系
- 第五章 原子与原子核
- 第一节 原子的结构
- 第二节 放射性元素的衰变
- 第三节 核力与核反应方程
- 第四节 放射性同位素
- 第五节 裂变和聚变
