功和能教案
图片预览




文档简介
功和能
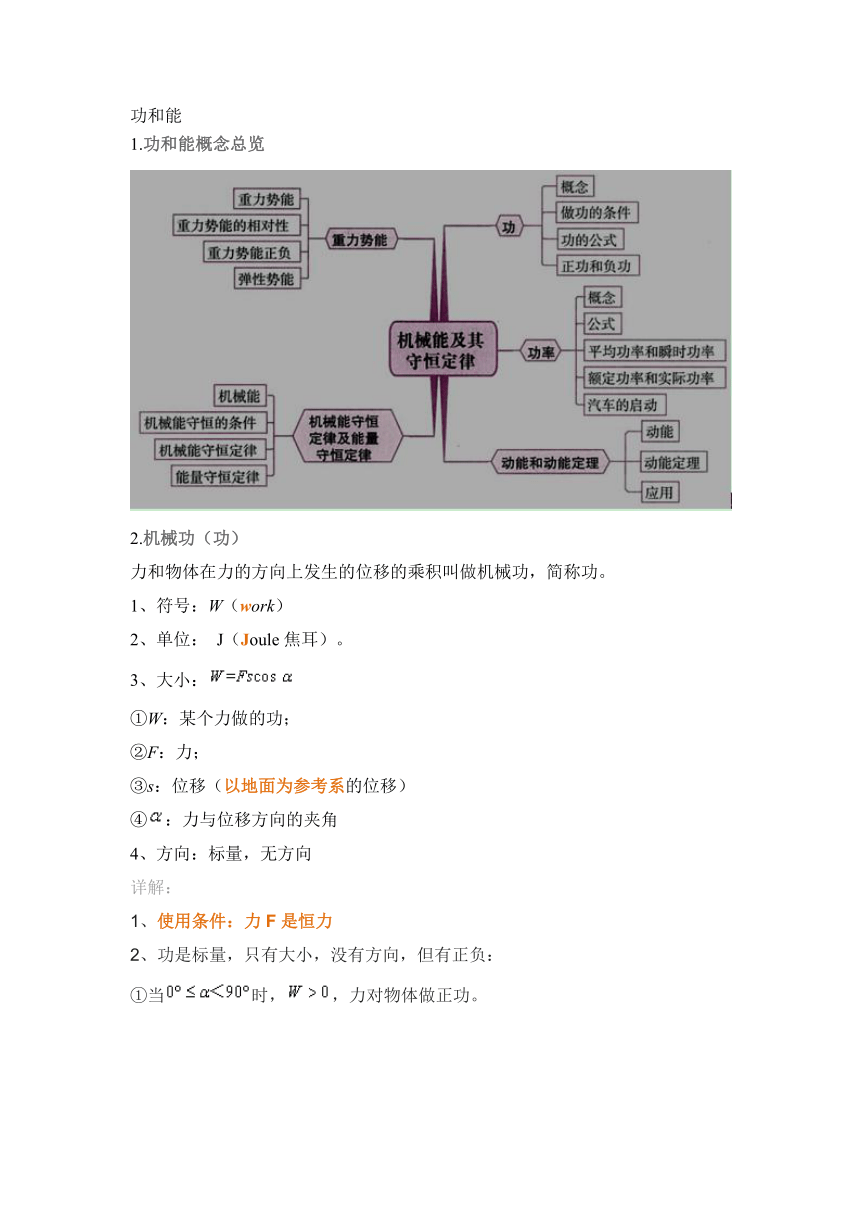
1.功和能概念总览
2.机械功(功)
力和物体在力的方向上发生的位移的乘积叫做机械功,简称功。
1、符号:W(work)
2、单位: J(Joule焦耳)。
3、大小:
①W:某个力做的功;
②F:力;
③s:位移(以地面为参考系的位移)
④:力与位移方向的夹角
4、方向:标量,无方向
详解:
1、使用条件:力F是恒力
2、功是标量,只有大小,没有方向,但有正负:
①当时,,力对物体做正功。
②当时,,力对物体做负功,也称物体克服这个力做了功。
③当时,,力对物体不做功。
3、作用力与反作用力虽然等大、反向,但由于它们作用的对象不同,故位移关系不能确定。因此,作用力做功时,反作用力可能做功,也可能不做功,可能做正功,也可能做负功,数值上也不一定相等。
4、编者的理解:某个力做的功等于这个力与位移的乘积,乘以这个力与位移之间夹角的余弦值。研究某个力做的功即研究这个力对物体的运动是促进或是阻碍,与其他力的作用无关。
5.合力做功等于各力做功的代数和。即。
实例:
1、合力做的功,等于合力与位移的乘积,乘以合力与位移之间夹角的余弦值
2、摩擦力做功,等于摩擦力与位移的乘积,乘以摩擦力与位移之间夹角的余弦值。
3、分析摩擦力做功严格按照功的公式进行分析,摩擦力阻碍的是相对接触面的运动,而不一定阻碍相对地面的运动,而做功公式中的位移是相对地面而言,所以摩擦力可以做正功,可以做负功,也可以不做功。
3.能量的转化
能量守恒定律:能量既不能凭空产生,也不能凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,而在能量的转化或转移过程中,能的总量保持不变。
1.某种形式的能量减少,一定存在其他形式的能量增加,且减少量和增加量相等。
2.某个物体的能量减少,一定存在别的物体的能量增加,且减少量和增加量相等。
详解:
1.能量守恒定律指出,能量不能被创造或消灭,只能从一个物体转移到另一个物体,或者从一种形式转化为另一种形式。在大多数情况下,能量最终都转化为内能。
2.内能总是自动地从高温物体向低温物体转移,而不会倒过来自动地从低温物体向高温物体转移。
3.热机效率不可能达到100%。
4.机械效率
人类发明和使用各种机械的目的,就是为了用它来代替人力做功,甚至完成超越人力的工作。
功(机械功)的原理:使用任何机械时,动力对机械所做的功总是等于机械克服阻力所做的功。公式:,或
机械效率是表示机械做功或利用该机械实现能量转化的有效程度的物理量。可表示为:。
详解:
只有在不考虑摩擦阻力和其他额外阻力(如机械本身所受重力)的理想情况下,(或)才等于(或);而在实际情况中,(或)必不为零,(或)总是小于(或),所以机械效率总小于1。
实例:
自行车的发明使人们以车代步,既省力又提高了速度。但是并不省功,有用功部分是人做的部分,以车代步不仅要对人做功,还要对车做功,所以使用机械做功机械效率总小于1。
5.功能关系
做功的过程就是能量转化的过程,做多少功就有多少某种形式的能转化为其他形式的能,功是能量转化的量度。
1.如果一个物体能够对别的物体做功,我们就说这个物体具有能量。
2.功和能量总是相互伴随的。
3.做功时消耗的能量并没有消失,而是发生了转化。
4.我们可以用做功的多少来量度在做功过程中有多少能量发生了转化。
5.机械做功只能将能量从一个物体转移到另一个物体,或者将一种形式的能量转化为另一种形式的能量。
详解:
无
实例:
1、合外力对物体做正功:其他形式的能转化为物体的动能;
2、重力对物体做正功:重力势能转化为其他形式的能;
3、弹簧弹力对做正功:弹性势能转化为其他形式的能
6.功率
表示做功快慢的物理量叫做功率。
1.符号:P(power)
2.单位:W(watt瓦特),1J/s=1W
3.公式:
4.方向:标量,只有大小,没有方向。
详解:
功率表示做功的快慢
7.额定功率和实际功率
额定功率:机械长时间工作的最大允许功率。机械的额定功率在出厂时已给定。
实际功率:机械实际输出的功率。机械正常工作时输出功率应在(额定功率)之间。
详解:
无
实例:
本电器的额定功率为350W。
8.平均功率和瞬时功率
1.平均功率:物体在一段时间或位移内做功的功率的平均值
2.瞬时功率:物体在某个时刻或某个位置的功率(为与之间的夹角)
详解:
仅适用于平均功率的计算。
实例:
1.起重机吊起一质量为200Kg的货物使其从静止开始竖直匀加速上升,经过2秒后,货物的速度达到,则起重机在这2秒内起吊货物的功率是多大?
解:拉力在2秒内的功率指的是平均功率,而不是2秒末的瞬时功率。
,,
由于F与的在同一方向上,故
2.从空中以40m/s的初速度平抛一个重10N的物体,物体在空中运动3S落地,不计空气阻力,求落地时重力的功率。
解:设物体在竖直方向做自由落体运动,3s末物体的竖直方向速度
末的瞬时功率
9.机车的起动分析
机车的起动分析:
对机车来说,牵引力F和v共线,故有。
1、当P一定时,F与速度v成反比,此时要增大牵引力,只有降低运动速度。
若运动过程中所受阻力f不变,则图象如图所示:
这一动态过程可用如下方框图表示:
2、当F一定时,P与速度v成正比,速度越大,机械功率越大,但不得超过机械的额定功率。
若运动过程中所受阻力f不变,则v-t图象如图所示:
这一动态过程可用如下方框图表示:
详解:
无
实例:
1.质量为的小汽车,以恒定功率行驶在平直公路上的最大速度,开上每前进20m升高1m的斜坡时最大速度。假定汽车所受摩擦阻力恒定。求:
①摩擦阻力的大小。
②汽车发动机的恒定功率。
解:设汽车的恒定功率为P,摩擦阻力为f,斜坡倾斜角为θ,汽车以恒定功率行驶,当速度达到最大时,应有,,汽车在平直公路上行驶达到最大速度时,,故;
汽车上坡时达到最大速度时,,;
汽车下坡时达到最大速度时,,;
由几何关系得
由上几式联立得,
2.额定功率为80kw的汽车,在平直的公路上行驶的最大速度是20m/s,汽车的质量是2t,如果汽车从静止开始做匀加速直线运动,加速度为2m/s2 ,运动过程中阻力不变。
①汽车受到的阻力多大?
②汽车匀加速能达到的最大速度?(体现匀变速直线运动的最大速度)
③汽车2s时达到的速度?(体现速度还没到最大时)
解:①汽车以额定功率行驶,当牵引力F等于阻力f时,汽车的速度达到最大,由
可得汽车所受的阻力为
②设汽车做匀加速运动时,牵引力大小为,故有,代入数据解得
汽车匀加速所能达到的最大速度为
③汽车维持匀加速的时间为
2s<5s,故2s时汽车还在做匀加速运动
10.动能
物体由于运动而具有的能量叫动能。
1.符号:
2.单位:焦,J
3.大小:
4.方向:标量,只有大小,没有方向
详解:
1.相对性:动能是一个状态量,与某一时刻或位置对应。
2.由于速度具有相对性,故动能也具有相对性,一般取地面为参考系。
3.动能与速度大小的平方成正比,与速度方向无关。一个物体动能不变,而速度可能改变;物体的速度不变,则动能一定不变。
11.动能定理
合外力对物体所做的功等于物体动能的改变。这个结论就叫做动能定理。
1.
:合力做功,
:末动能,
:初动能,
m:质量,
:初速度,
:末速度。
1.,则表示合外力作为动力对物体做功,物体的动能增加,。,则表示合外力作为阻力对物体做功,物体的动能减少,。
2.动能定理适用于物体的直线运动,也适用于曲线运动;适用于恒力做功,也适用于变力做功。力可以是各种性质的力,既可以同时作用,也可以分段作用。
3.动能定理的计算式为标量式,v、s一般选地面为参考系。
详解:
动能定理分析步骤:
①确定本题研究对象;
②研究对象的轨迹,确定初位置和末位置;
③从初位置到末位置过程的受力分析;
④列出动能定理的式子:
实例:
大马哈鱼总是要逆流而上游到乌苏里江上游产卵,游程中有时还要跃上瀑布。这种鱼跃出水面的速度可达36 km/h,它最高可以跃上多高的瀑布 (取,不计空气阻力)
分析过程:
①确定本题研究对象:大马哈鱼
②研究对象的轨迹,确定初位置在水面,速度为,末位置是最高点;
③从初位置到末位置过程的受力分析:大马哈鱼只受到重力作用
④列出动能定理的式子:
解题过程:
大马哈鱼向上跃到达最高点的过程中,设初末速度分别为,,
根据动能定理,代入数据
解得:
12.势能
人们把由相对位置决定的能称为势能。
详解:
无
实例:
重力势能、弹性势能、分子势能
13.重力势能
地球上的物体具有跟它的高度有关的能量,叫做重力势能。
1.符号:
2.单位:J
3.大小:
4.方向:标量,但有正负之分,其正负表示比物体在零势能面所具有的重力势能是多还是少。
详解:
1.重力势能:是由物体和地球之间的相互作用及相对位置所决定的势能。
2.重力势能是地球和物体组成的系统所共有的,而不是物体单独具有的。
3.重力势能的大小和零势能面的选取有关。
4.两点之间的重力势能之差与零势能面的选取无关。
实例:
1.设取向上为正。若以地面为零势能点则下落点重力势能为正,若以瀑布下落点为零势能点则下落点重力势能为0,地面重力势能为负。注意此处的正负只表示方向。
2.物体在桌面与地面之间的势能与零势能点选取桌面还是地面无关。
14.重力做功与重力势能变化的关系
详解:
1、公式推导:
2、重力对物体做多少功,物体的重力势能就减少多少;重力对物体做多少负功(物体克服重力做多少功),物体的重力势能就增加多少。
3、物体运动时,重力对它做的功只跟它的起点和终点位置的高度差有关,而跟物体运动的路径无关。
15.弹性势能
物理学中,把物体因为发生弹性形变而具有的能叫做弹性势能。
1.符号:
2.单位:焦耳,J
3.大小:
:弹簧的劲度系数,国际单位制单位N/m
:弹簧的形变量,国际单位制单位是m
4.方向:标量
实例:
拉开弹弓、上紧钟表的发条等,都是让物体具有弹性势能。
16.微元法
微元法:在处理问题时,从对事物的极小部分(微元)分析入手,达到解决事物整体的方法。是一种深刻的思维方法,是先分割逼近,找到规律,再累计求和,达到了解整体。
详解:
无
实例:
如图所示,弹簧弹力F与弹簧形变量l成线性关系,如果将形变量l取很多份,每一份上弹簧的弹力就可以当作恒力处理,由W=F·s,知很多个矩形“面积”的数值和就与弹力的功大小相等,.因为弹力做功等于弹性势能的改变量,所以这一过程中弹性势能改变了。如果弹簧的自由长度为零势能点,弹性势能的表达式为,式中l为相对自由长度的形变量。
17.机械能
机械能:.动能和势能统称为机械能,;
机械能守恒定律:在只有重力(或弹簧的弹力)做功的情况下,物体的动能和重力势能(或弹性势能)发生相互转化,但机械能的总量保持不变,;
详解:
1.机械能守恒定律的表达形式比较多,常见有三种:
A.初态机械能等于末态机械能:
B.动能的增加量等于势能的减少量:
C.对A、B两个物体组成的系统,还可以表示为A增加的机械能等于B减少的机械能:
2.选择A形式必需指明重力势能的参考平面,而其他两种形式则不必。
3.判断方法:
①用做功来判断:分析物体或物体系的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力或弹簧的弹力做功,没有其他力做功,则机械能守恒。
②用能量转化来判定:若物体系中只有动能和势能的相互转化而无机械能与其他形式的能的转化,则物体系机械能守恒。
③对一些绳子突然绷紧、物体间碰撞、爆炸、反冲等问题机械能一般不守恒,除非题目特别说明或暗示,完全非弹性碰撞过程机械能不守恒。
4.解题步骤:
①根据题意,确定研究对象,可以是单体和地球组成的系统,也可以是多体和地球组成的系统。
②明确研究过程,分析研究对象的受力情况,分清各力做功情况,判断是否符合机械能守恒的条件。
③确定势能的零势能面(或零势能点),计算在研究过程中的始末状态的机械能。
④根据机械能守恒定律列方程,并结合其他方程求解。
实例:
1.在撑杆跳或者蹦床等类似的运动中,整个过程只有重力或弹力做功,没有其他力做功,则撑杆、蹦床和运动员组成的系统机械能守恒。
2.只有动能和势能的相互转化而无机械能与其他形式的能的转化,则物体系机械能守恒。
3.火箭发射时,由于非保守力作用,致使机械能转换为热能、声能、化学能等其他形式的能量,或者其他形式的能量转换为机械能。
4.长为L的均匀链条,放在光滑的水平桌面上,且使其长度的1/4垂在桌边,如图所示,松手后链条从静止开始沿桌边下滑,则链条滑至刚刚离开桌边时的速度大小为多大?
解析:链条下滑时,因桌面光滑,没有摩擦力做功。整根链条总的机械能守恒,可用机械能守恒定律求解。设整根链条质量为m,则单位长度质量(质量线密度)为,
设桌面重力势能为零,由机械能守恒定律得:
18.机械能守恒定律的重要推论
重力和弹簧弹力以外的力做的功等于物体机械能的变化量
详解:
重力、弹簧弹力以外的所有外力做多少功,物体的机械能就增加多少;克服重力、弹簧弹力以外的所有外力做多少功物体的机械能就减少多少。
1.功和能概念总览
2.机械功(功)
力和物体在力的方向上发生的位移的乘积叫做机械功,简称功。
1、符号:W(work)
2、单位: J(Joule焦耳)。
3、大小:
①W:某个力做的功;
②F:力;
③s:位移(以地面为参考系的位移)
④:力与位移方向的夹角
4、方向:标量,无方向
详解:
1、使用条件:力F是恒力
2、功是标量,只有大小,没有方向,但有正负:
①当时,,力对物体做正功。
②当时,,力对物体做负功,也称物体克服这个力做了功。
③当时,,力对物体不做功。
3、作用力与反作用力虽然等大、反向,但由于它们作用的对象不同,故位移关系不能确定。因此,作用力做功时,反作用力可能做功,也可能不做功,可能做正功,也可能做负功,数值上也不一定相等。
4、编者的理解:某个力做的功等于这个力与位移的乘积,乘以这个力与位移之间夹角的余弦值。研究某个力做的功即研究这个力对物体的运动是促进或是阻碍,与其他力的作用无关。
5.合力做功等于各力做功的代数和。即。
实例:
1、合力做的功,等于合力与位移的乘积,乘以合力与位移之间夹角的余弦值
2、摩擦力做功,等于摩擦力与位移的乘积,乘以摩擦力与位移之间夹角的余弦值。
3、分析摩擦力做功严格按照功的公式进行分析,摩擦力阻碍的是相对接触面的运动,而不一定阻碍相对地面的运动,而做功公式中的位移是相对地面而言,所以摩擦力可以做正功,可以做负功,也可以不做功。
3.能量的转化
能量守恒定律:能量既不能凭空产生,也不能凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体转移到另一个物体,而在能量的转化或转移过程中,能的总量保持不变。
1.某种形式的能量减少,一定存在其他形式的能量增加,且减少量和增加量相等。
2.某个物体的能量减少,一定存在别的物体的能量增加,且减少量和增加量相等。
详解:
1.能量守恒定律指出,能量不能被创造或消灭,只能从一个物体转移到另一个物体,或者从一种形式转化为另一种形式。在大多数情况下,能量最终都转化为内能。
2.内能总是自动地从高温物体向低温物体转移,而不会倒过来自动地从低温物体向高温物体转移。
3.热机效率不可能达到100%。
4.机械效率
人类发明和使用各种机械的目的,就是为了用它来代替人力做功,甚至完成超越人力的工作。
功(机械功)的原理:使用任何机械时,动力对机械所做的功总是等于机械克服阻力所做的功。公式:,或
机械效率是表示机械做功或利用该机械实现能量转化的有效程度的物理量。可表示为:。
详解:
只有在不考虑摩擦阻力和其他额外阻力(如机械本身所受重力)的理想情况下,(或)才等于(或);而在实际情况中,(或)必不为零,(或)总是小于(或),所以机械效率总小于1。
实例:
自行车的发明使人们以车代步,既省力又提高了速度。但是并不省功,有用功部分是人做的部分,以车代步不仅要对人做功,还要对车做功,所以使用机械做功机械效率总小于1。
5.功能关系
做功的过程就是能量转化的过程,做多少功就有多少某种形式的能转化为其他形式的能,功是能量转化的量度。
1.如果一个物体能够对别的物体做功,我们就说这个物体具有能量。
2.功和能量总是相互伴随的。
3.做功时消耗的能量并没有消失,而是发生了转化。
4.我们可以用做功的多少来量度在做功过程中有多少能量发生了转化。
5.机械做功只能将能量从一个物体转移到另一个物体,或者将一种形式的能量转化为另一种形式的能量。
详解:
无
实例:
1、合外力对物体做正功:其他形式的能转化为物体的动能;
2、重力对物体做正功:重力势能转化为其他形式的能;
3、弹簧弹力对做正功:弹性势能转化为其他形式的能
6.功率
表示做功快慢的物理量叫做功率。
1.符号:P(power)
2.单位:W(watt瓦特),1J/s=1W
3.公式:
4.方向:标量,只有大小,没有方向。
详解:
功率表示做功的快慢
7.额定功率和实际功率
额定功率:机械长时间工作的最大允许功率。机械的额定功率在出厂时已给定。
实际功率:机械实际输出的功率。机械正常工作时输出功率应在(额定功率)之间。
详解:
无
实例:
本电器的额定功率为350W。
8.平均功率和瞬时功率
1.平均功率:物体在一段时间或位移内做功的功率的平均值
2.瞬时功率:物体在某个时刻或某个位置的功率(为与之间的夹角)
详解:
仅适用于平均功率的计算。
实例:
1.起重机吊起一质量为200Kg的货物使其从静止开始竖直匀加速上升,经过2秒后,货物的速度达到,则起重机在这2秒内起吊货物的功率是多大?
解:拉力在2秒内的功率指的是平均功率,而不是2秒末的瞬时功率。
,,
由于F与的在同一方向上,故
2.从空中以40m/s的初速度平抛一个重10N的物体,物体在空中运动3S落地,不计空气阻力,求落地时重力的功率。
解:设物体在竖直方向做自由落体运动,3s末物体的竖直方向速度
末的瞬时功率
9.机车的起动分析
机车的起动分析:
对机车来说,牵引力F和v共线,故有。
1、当P一定时,F与速度v成反比,此时要增大牵引力,只有降低运动速度。
若运动过程中所受阻力f不变,则图象如图所示:
这一动态过程可用如下方框图表示:
2、当F一定时,P与速度v成正比,速度越大,机械功率越大,但不得超过机械的额定功率。
若运动过程中所受阻力f不变,则v-t图象如图所示:
这一动态过程可用如下方框图表示:
详解:
无
实例:
1.质量为的小汽车,以恒定功率行驶在平直公路上的最大速度,开上每前进20m升高1m的斜坡时最大速度。假定汽车所受摩擦阻力恒定。求:
①摩擦阻力的大小。
②汽车发动机的恒定功率。
解:设汽车的恒定功率为P,摩擦阻力为f,斜坡倾斜角为θ,汽车以恒定功率行驶,当速度达到最大时,应有,,汽车在平直公路上行驶达到最大速度时,,故;
汽车上坡时达到最大速度时,,;
汽车下坡时达到最大速度时,,;
由几何关系得
由上几式联立得,
2.额定功率为80kw的汽车,在平直的公路上行驶的最大速度是20m/s,汽车的质量是2t,如果汽车从静止开始做匀加速直线运动,加速度为2m/s2 ,运动过程中阻力不变。
①汽车受到的阻力多大?
②汽车匀加速能达到的最大速度?(体现匀变速直线运动的最大速度)
③汽车2s时达到的速度?(体现速度还没到最大时)
解:①汽车以额定功率行驶,当牵引力F等于阻力f时,汽车的速度达到最大,由
可得汽车所受的阻力为
②设汽车做匀加速运动时,牵引力大小为,故有,代入数据解得
汽车匀加速所能达到的最大速度为
③汽车维持匀加速的时间为
2s<5s,故2s时汽车还在做匀加速运动
10.动能
物体由于运动而具有的能量叫动能。
1.符号:
2.单位:焦,J
3.大小:
4.方向:标量,只有大小,没有方向
详解:
1.相对性:动能是一个状态量,与某一时刻或位置对应。
2.由于速度具有相对性,故动能也具有相对性,一般取地面为参考系。
3.动能与速度大小的平方成正比,与速度方向无关。一个物体动能不变,而速度可能改变;物体的速度不变,则动能一定不变。
11.动能定理
合外力对物体所做的功等于物体动能的改变。这个结论就叫做动能定理。
1.
:合力做功,
:末动能,
:初动能,
m:质量,
:初速度,
:末速度。
1.,则表示合外力作为动力对物体做功,物体的动能增加,。,则表示合外力作为阻力对物体做功,物体的动能减少,。
2.动能定理适用于物体的直线运动,也适用于曲线运动;适用于恒力做功,也适用于变力做功。力可以是各种性质的力,既可以同时作用,也可以分段作用。
3.动能定理的计算式为标量式,v、s一般选地面为参考系。
详解:
动能定理分析步骤:
①确定本题研究对象;
②研究对象的轨迹,确定初位置和末位置;
③从初位置到末位置过程的受力分析;
④列出动能定理的式子:
实例:
大马哈鱼总是要逆流而上游到乌苏里江上游产卵,游程中有时还要跃上瀑布。这种鱼跃出水面的速度可达36 km/h,它最高可以跃上多高的瀑布 (取,不计空气阻力)
分析过程:
①确定本题研究对象:大马哈鱼
②研究对象的轨迹,确定初位置在水面,速度为,末位置是最高点;
③从初位置到末位置过程的受力分析:大马哈鱼只受到重力作用
④列出动能定理的式子:
解题过程:
大马哈鱼向上跃到达最高点的过程中,设初末速度分别为,,
根据动能定理,代入数据
解得:
12.势能
人们把由相对位置决定的能称为势能。
详解:
无
实例:
重力势能、弹性势能、分子势能
13.重力势能
地球上的物体具有跟它的高度有关的能量,叫做重力势能。
1.符号:
2.单位:J
3.大小:
4.方向:标量,但有正负之分,其正负表示比物体在零势能面所具有的重力势能是多还是少。
详解:
1.重力势能:是由物体和地球之间的相互作用及相对位置所决定的势能。
2.重力势能是地球和物体组成的系统所共有的,而不是物体单独具有的。
3.重力势能的大小和零势能面的选取有关。
4.两点之间的重力势能之差与零势能面的选取无关。
实例:
1.设取向上为正。若以地面为零势能点则下落点重力势能为正,若以瀑布下落点为零势能点则下落点重力势能为0,地面重力势能为负。注意此处的正负只表示方向。
2.物体在桌面与地面之间的势能与零势能点选取桌面还是地面无关。
14.重力做功与重力势能变化的关系
详解:
1、公式推导:
2、重力对物体做多少功,物体的重力势能就减少多少;重力对物体做多少负功(物体克服重力做多少功),物体的重力势能就增加多少。
3、物体运动时,重力对它做的功只跟它的起点和终点位置的高度差有关,而跟物体运动的路径无关。
15.弹性势能
物理学中,把物体因为发生弹性形变而具有的能叫做弹性势能。
1.符号:
2.单位:焦耳,J
3.大小:
:弹簧的劲度系数,国际单位制单位N/m
:弹簧的形变量,国际单位制单位是m
4.方向:标量
实例:
拉开弹弓、上紧钟表的发条等,都是让物体具有弹性势能。
16.微元法
微元法:在处理问题时,从对事物的极小部分(微元)分析入手,达到解决事物整体的方法。是一种深刻的思维方法,是先分割逼近,找到规律,再累计求和,达到了解整体。
详解:
无
实例:
如图所示,弹簧弹力F与弹簧形变量l成线性关系,如果将形变量l取很多份,每一份上弹簧的弹力就可以当作恒力处理,由W=F·s,知很多个矩形“面积”的数值和就与弹力的功大小相等,.因为弹力做功等于弹性势能的改变量,所以这一过程中弹性势能改变了。如果弹簧的自由长度为零势能点,弹性势能的表达式为,式中l为相对自由长度的形变量。
17.机械能
机械能:.动能和势能统称为机械能,;
机械能守恒定律:在只有重力(或弹簧的弹力)做功的情况下,物体的动能和重力势能(或弹性势能)发生相互转化,但机械能的总量保持不变,;
详解:
1.机械能守恒定律的表达形式比较多,常见有三种:
A.初态机械能等于末态机械能:
B.动能的增加量等于势能的减少量:
C.对A、B两个物体组成的系统,还可以表示为A增加的机械能等于B减少的机械能:
2.选择A形式必需指明重力势能的参考平面,而其他两种形式则不必。
3.判断方法:
①用做功来判断:分析物体或物体系的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力或弹簧的弹力做功,没有其他力做功,则机械能守恒。
②用能量转化来判定:若物体系中只有动能和势能的相互转化而无机械能与其他形式的能的转化,则物体系机械能守恒。
③对一些绳子突然绷紧、物体间碰撞、爆炸、反冲等问题机械能一般不守恒,除非题目特别说明或暗示,完全非弹性碰撞过程机械能不守恒。
4.解题步骤:
①根据题意,确定研究对象,可以是单体和地球组成的系统,也可以是多体和地球组成的系统。
②明确研究过程,分析研究对象的受力情况,分清各力做功情况,判断是否符合机械能守恒的条件。
③确定势能的零势能面(或零势能点),计算在研究过程中的始末状态的机械能。
④根据机械能守恒定律列方程,并结合其他方程求解。
实例:
1.在撑杆跳或者蹦床等类似的运动中,整个过程只有重力或弹力做功,没有其他力做功,则撑杆、蹦床和运动员组成的系统机械能守恒。
2.只有动能和势能的相互转化而无机械能与其他形式的能的转化,则物体系机械能守恒。
3.火箭发射时,由于非保守力作用,致使机械能转换为热能、声能、化学能等其他形式的能量,或者其他形式的能量转换为机械能。
4.长为L的均匀链条,放在光滑的水平桌面上,且使其长度的1/4垂在桌边,如图所示,松手后链条从静止开始沿桌边下滑,则链条滑至刚刚离开桌边时的速度大小为多大?
解析:链条下滑时,因桌面光滑,没有摩擦力做功。整根链条总的机械能守恒,可用机械能守恒定律求解。设整根链条质量为m,则单位长度质量(质量线密度)为,
设桌面重力势能为零,由机械能守恒定律得:
18.机械能守恒定律的重要推论
重力和弹簧弹力以外的力做的功等于物体机械能的变化量
详解:
重力、弹簧弹力以外的所有外力做多少功,物体的机械能就增加多少;克服重力、弹簧弹力以外的所有外力做多少功物体的机械能就减少多少。
