同底数幂的除法[上学期]
图片预览






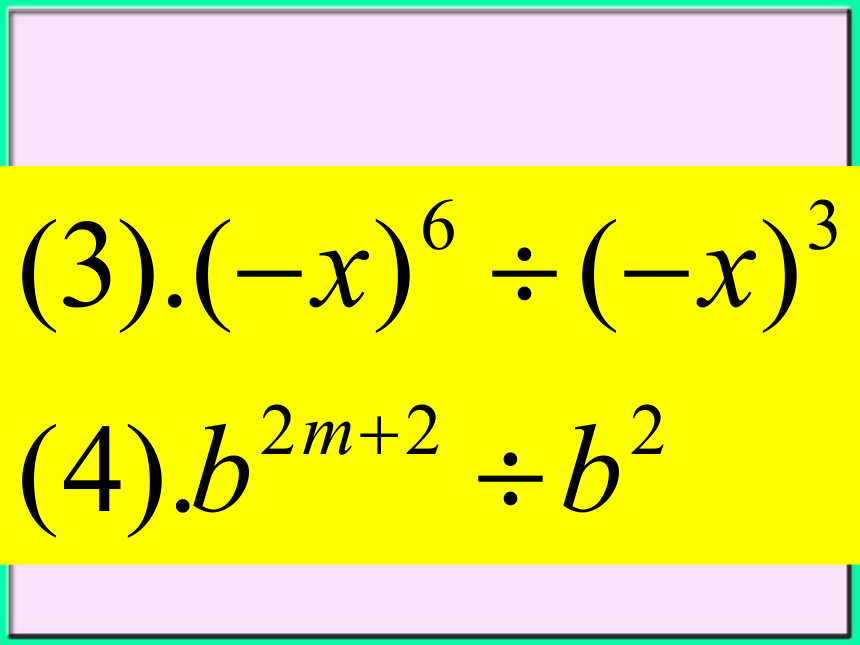


文档简介
课件27张PPT。同底数幂的除法复习同底数幂相乘的法则:
同底数幂相乘,底数不变,
指数相加。
即aman=am+n(m,n都是正整数)问题1:同底数幂的乘法法则的内容是什么?应如何表示? 练习1、计算:
(1)(-2)3?(-2)2; (2) a5?a2 ;
(3)(-2)4?22 ; (4)-a2?a3;
(5)(-a)2?a3; (6)-a2?(-a)3;
(7)(a-b)?(a-b)2 ; (8)3a5+a2?a4 -2a3?a2。
2、填空:
(1)( )×103= 105; (2)23× ( )= 27;
(3)a4 × ( )= a9;
(4) ( )×(-a)2 = (-a)10 a510224(-a)8问题2:观察下列四小题中的两个幂有什么共同之处?
(1)105÷103;
(2)27 ÷ 23;
(3)a9÷ a4;
(4)(-a)10 ÷ (-a) 2。问题3:请计算出上述各小题的结果。23× ( )= 27a4 × ( )= a9 ( ) ×(-a)2 =(-a)10a510224(-a)8( )×103= 105(1)105÷103=102; (2)27 ÷ 23=24;(3)a9÷ a4=a5;(4)(-a)10 ÷ (-a) 2=(-a)8=a8。新知:试一试:用你熟悉的方法计算:概 括:一般地,设m、n为正整数,m>n,a≠0,有即:同底数幂相除,底数不变,指数相减。例1 计算:做一做:计算下列各式,并说明理由(m>n). 我们规定:例题分析:点评:
(1)底数可以是数,也可以是单
项式、多项式;
(2)商的结果若能化简,则要求
化简。 例题分析:注:底数不同时,要化为相同的.方法一:先化为同底数幂,再运算;方法二:先确定商的符号,再运算;注意:
1、题目没有特殊说明结果形式要求的,都要化到最简。
2、本教科书中,如果没有特别说明的,含有字母的除式均不零。1、
2、出题意图:(1)注意符号的确定;
(2)注意底数的变化;
(3)挑战新高:计算:整体思想计算:1、
2、
3、
4、出题意图:这是整式的混合运算,要根据混合运算的法则:先乘方,后乘除,再加减,有括号先算括号的运算顺序进行。综合运用: 如图表示的是经染色的洋葱根尖细
胞,细胞每分裂一次,1个细胞变成2个
细胞. 洋葱根尖细胞分裂的一个周期大
约是12时, 个洋葱根尖
细胞经过分裂后,变成
个细胞大约需要多少时间?想一想练一练1. 计算:口答:3、填空:
(1)x7.( )=x8; (2)( ).a3=a8;
(3)b4.b3.( )=b21; (4)c8÷( )=c5;
(5)( ) ÷ a3 = a4 ; (6)(-a)7 ÷ ( )= -a4xa5b14c32、计算
(1)t2m+3 ÷ t2(m是正整数); (2)a8÷ (-a)5;
(3) (-a)4÷ a3 ;
(4) (a-b)5÷(b-a)2; (5) (a-b)9÷(b-a)3。a7a34、判断:
(1)a3·a2=a3×2=a6; (2)a5·a3=a5+3=a8;
(3)a9÷a3=a9÷3=a3; (4)a6÷ a3 = a2;
(5)a5÷ a = a5; (6)-a6÷ a5 = -1。
5、计算下列各式:
(1) x5÷x4÷x; (2)y8÷y6÷y2;
(3)a5÷a4.a2 ; (4)y8÷(y6÷y2);
(5)(a3)5÷(a2)3; (6)xn-1÷x·x3-n;
(7)-(y5?y2)÷(y3?y4);(8)(-x)8÷(-x)2-x4?x2。例 2 . 计算:探索与思考归纳小结1、本节课我们学习了那些内容?同底数幂的除法性质:底数 ,指数 。 不变相减2、已学过的幂运算性质:
(1)am·an=am+n (a≠0、 m、n为正整数)
(2)am÷an=am-n (a≠0 、m、n为正整数且m>n)
(3)(am)n=amn (a≠0、 m、n为正整数)
(4)(ab)n=anbn (a≠0 、m、n为正整数)小测:知识拓展(1)若n为正整数, 则 n =____,则m =_____布置作业:练习作业卷1再见
同底数幂相乘,底数不变,
指数相加。
即aman=am+n(m,n都是正整数)问题1:同底数幂的乘法法则的内容是什么?应如何表示? 练习1、计算:
(1)(-2)3?(-2)2; (2) a5?a2 ;
(3)(-2)4?22 ; (4)-a2?a3;
(5)(-a)2?a3; (6)-a2?(-a)3;
(7)(a-b)?(a-b)2 ; (8)3a5+a2?a4 -2a3?a2。
2、填空:
(1)( )×103= 105; (2)23× ( )= 27;
(3)a4 × ( )= a9;
(4) ( )×(-a)2 = (-a)10 a510224(-a)8问题2:观察下列四小题中的两个幂有什么共同之处?
(1)105÷103;
(2)27 ÷ 23;
(3)a9÷ a4;
(4)(-a)10 ÷ (-a) 2。问题3:请计算出上述各小题的结果。23× ( )= 27a4 × ( )= a9 ( ) ×(-a)2 =(-a)10a510224(-a)8( )×103= 105(1)105÷103=102; (2)27 ÷ 23=24;(3)a9÷ a4=a5;(4)(-a)10 ÷ (-a) 2=(-a)8=a8。新知:试一试:用你熟悉的方法计算:概 括:一般地,设m、n为正整数,m>n,a≠0,有即:同底数幂相除,底数不变,指数相减。例1 计算:做一做:计算下列各式,并说明理由(m>n). 我们规定:例题分析:点评:
(1)底数可以是数,也可以是单
项式、多项式;
(2)商的结果若能化简,则要求
化简。 例题分析:注:底数不同时,要化为相同的.方法一:先化为同底数幂,再运算;方法二:先确定商的符号,再运算;注意:
1、题目没有特殊说明结果形式要求的,都要化到最简。
2、本教科书中,如果没有特别说明的,含有字母的除式均不零。1、
2、出题意图:(1)注意符号的确定;
(2)注意底数的变化;
(3)挑战新高:计算:整体思想计算:1、
2、
3、
4、出题意图:这是整式的混合运算,要根据混合运算的法则:先乘方,后乘除,再加减,有括号先算括号的运算顺序进行。综合运用: 如图表示的是经染色的洋葱根尖细
胞,细胞每分裂一次,1个细胞变成2个
细胞. 洋葱根尖细胞分裂的一个周期大
约是12时, 个洋葱根尖
细胞经过分裂后,变成
个细胞大约需要多少时间?想一想练一练1. 计算:口答:3、填空:
(1)x7.( )=x8; (2)( ).a3=a8;
(3)b4.b3.( )=b21; (4)c8÷( )=c5;
(5)( ) ÷ a3 = a4 ; (6)(-a)7 ÷ ( )= -a4xa5b14c32、计算
(1)t2m+3 ÷ t2(m是正整数); (2)a8÷ (-a)5;
(3) (-a)4÷ a3 ;
(4) (a-b)5÷(b-a)2; (5) (a-b)9÷(b-a)3。a7a34、判断:
(1)a3·a2=a3×2=a6; (2)a5·a3=a5+3=a8;
(3)a9÷a3=a9÷3=a3; (4)a6÷ a3 = a2;
(5)a5÷ a = a5; (6)-a6÷ a5 = -1。
5、计算下列各式:
(1) x5÷x4÷x; (2)y8÷y6÷y2;
(3)a5÷a4.a2 ; (4)y8÷(y6÷y2);
(5)(a3)5÷(a2)3; (6)xn-1÷x·x3-n;
(7)-(y5?y2)÷(y3?y4);(8)(-x)8÷(-x)2-x4?x2。例 2 . 计算:探索与思考归纳小结1、本节课我们学习了那些内容?同底数幂的除法性质:底数 ,指数 。 不变相减2、已学过的幂运算性质:
(1)am·an=am+n (a≠0、 m、n为正整数)
(2)am÷an=am-n (a≠0 、m、n为正整数且m>n)
(3)(am)n=amn (a≠0、 m、n为正整数)
(4)(ab)n=anbn (a≠0 、m、n为正整数)小测:知识拓展(1)若n为正整数, 则 n =____,则m =_____布置作业:练习作业卷1再见
