幂的乘方[上学期]
图片预览


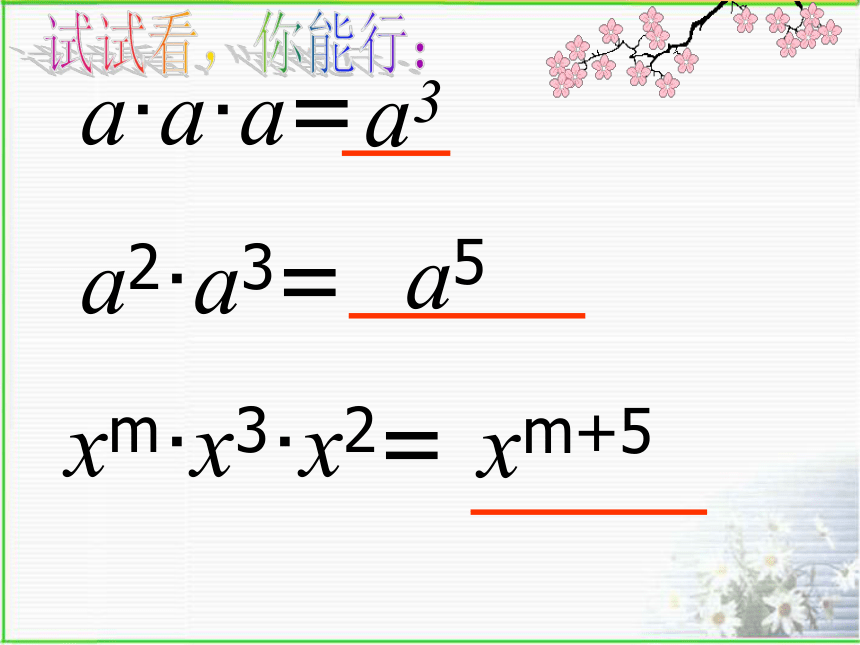









文档简介
课件33张PPT。课前复习:同底数幂的乘法:
am · an = am+n (m、n为正整数) 练 习am+ma3+3+3a2·a3=a5xm·x3·x2=xm+5试试看,你能行:a·a·a=a3根据 意义和同底数幂的乘法法则填空:乘方求几个相同因数的积的运算探索思考2.幂的乘方{{探究:幂的乘方,底数不变,指数相乘。下式从左边到右边是怎样变化的?幂的乘方法则想一想读作:a的m次幂的n次方例1 计算:解:练习:计算⑴(23m)2⑵ (a2m)3n⑶ (a2m+1)5 猜一猜,试一试:看谁答得快! (24)3= (5) (-a3)2=
(2) (a5)3= (6) (-a2)3=
(3) [ (-3)5 ]2= (7) [(1-2b)3]3=
(4) [ (-a)3 ]5= (8) [ (a3)2 ]4=212a15310a6-a6a24-a15(1-2b)9多重乘方:小明的解答有错误吗?(1) (x3)3 = x6 ; a6 · a4 =a6+4= a10 .(x3 )3= x3×3=x9 . (2)a6 · a4 = a24 .××练习:下面的式子成立吗?如果不对,应怎样改正?(1)(2)(3)√×××抢答题看谁说的好!下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) (-b3)m=(-bm)3 ( )
× × × × ×能力挑战1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋!⑴ a8 + (a2)4 ⑵ a3 . (a5)2
⑶ (x2 . x3)5 ⑷ (a2 . a)3 . (a2)3
⑸ (-a3)2 . a - 2a7
⑹ - ( - a2)6 – a (- a)3 . (- a2)4 计算:1.计算:
⑴ (a2)3 ⑵ a2·a3 ⑶ (y5)5 ⑷ y5·y52.计算:
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ -(xn)2· (x3)2m ⑷ (a2)3+a3 · a3要认真呀!课堂作业1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x(x5)m (D) xx5xmc变一变2.x14不可以写成( )
(A)x5(x3)3(B) (-x)(-x2)(-x3)(-x8) (C)(x7)7 (D) x3x4x5x2
C3.计算(-32)5-(-35)2的结果是( )
(A)0 (B) -2×310
(C)2×310 (D) -2×37
B4.下列说法中正确的是( )
(A)-xn等于(-x)n
(B)-xn与(-x)n互为相反数
(C)当n为奇数时-xn与(-x)n互为相反数
(D)当n为偶数时-xn与(-x)n互为相反数D5.若正方体棱长是(1+3a)3,则其体积是( )
(A)(1+3a)6 (B) (1+3a)9
(C)(1+3a)12 (D)(1+3a)27
B⑴ (an+1)2⑵ (am)3⑶ (410)5⑷ [(-1)3]4⑸ -4(a2)3⑹[(a+b)2]5⑺ (mn)n+1⑻ (x2a)3⑼ (y3)m+3抢答:(am)n=amn(an)m=anm,所以(am)n = (an)m合作学习幂的乘方法则的逆用:幂的乘方的逆运算:
(1).1010 = ( )2 = ( )5
(2) x13·x7 =x( ) =( )5 =( )4 =( )10
(3)a2m =( )2 =( )m (m为正整数)
105
10220x4x5x2ama2填一填1、若 a5 . (an)3 = a11,则n= ,
2、若 2n+3 = 64,则n= ,
3、已知 644×83 = 2n,则n= 。2333(4)设n为正整数,且x2n=2,求9(x3n)2 的值。
已知10a=2,10b=3,求102a+3b的值。
解:∵ x2n=2
∴ 9(x3n)2 = 9(x2n)3 = 9×23=72思考探索(我相信你一定会成功)⑴ 22与32⑶ 340与 430哪个
大呢?⑵ 43与53想: 340=( )想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m , n都是正整数本节课的收获??相加相乘不变
不变任何成果的取得都需要
付出艰苦的劳动!
am · an = am+n (m、n为正整数) 练 习am+ma3+3+3a2·a3=a5xm·x3·x2=xm+5试试看,你能行:a·a·a=a3根据 意义和同底数幂的乘法法则填空:乘方求几个相同因数的积的运算探索思考2.幂的乘方{{探究:幂的乘方,底数不变,指数相乘。下式从左边到右边是怎样变化的?幂的乘方法则想一想读作:a的m次幂的n次方例1 计算:解:练习:计算⑴(23m)2⑵ (a2m)3n⑶ (a2m+1)5 猜一猜,试一试:看谁答得快! (24)3= (5) (-a3)2=
(2) (a5)3= (6) (-a2)3=
(3) [ (-3)5 ]2= (7) [(1-2b)3]3=
(4) [ (-a)3 ]5= (8) [ (a3)2 ]4=212a15310a6-a6a24-a15(1-2b)9多重乘方:小明的解答有错误吗?(1) (x3)3 = x6 ; a6 · a4 =a6+4= a10 .(x3 )3= x3×3=x9 . (2)a6 · a4 = a24 .××练习:下面的式子成立吗?如果不对,应怎样改正?(1)(2)(3)√×××抢答题看谁说的好!下列各式对吗?请说出你的观点和理由:
(1) (a4)3=a7 ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) (-b3)m=(-bm)3 ( )
× × × × ×能力挑战1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋!⑴ a8 + (a2)4 ⑵ a3 . (a5)2
⑶ (x2 . x3)5 ⑷ (a2 . a)3 . (a2)3
⑸ (-a3)2 . a - 2a7
⑹ - ( - a2)6 – a (- a)3 . (- a2)4 计算:1.计算:
⑴ (a2)3 ⑵ a2·a3 ⑶ (y5)5 ⑷ y5·y52.计算:
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ -(xn)2· (x3)2m ⑷ (a2)3+a3 · a3要认真呀!课堂作业1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x(x5)m (D) xx5xmc变一变2.x14不可以写成( )
(A)x5(x3)3(B) (-x)(-x2)(-x3)(-x8) (C)(x7)7 (D) x3x4x5x2
C3.计算(-32)5-(-35)2的结果是( )
(A)0 (B) -2×310
(C)2×310 (D) -2×37
B4.下列说法中正确的是( )
(A)-xn等于(-x)n
(B)-xn与(-x)n互为相反数
(C)当n为奇数时-xn与(-x)n互为相反数
(D)当n为偶数时-xn与(-x)n互为相反数D5.若正方体棱长是(1+3a)3,则其体积是( )
(A)(1+3a)6 (B) (1+3a)9
(C)(1+3a)12 (D)(1+3a)27
B⑴ (an+1)2⑵ (am)3⑶ (410)5⑷ [(-1)3]4⑸ -4(a2)3⑹[(a+b)2]5⑺ (mn)n+1⑻ (x2a)3⑼ (y3)m+3抢答:(am)n=amn(an)m=anm,所以(am)n = (an)m合作学习幂的乘方法则的逆用:幂的乘方的逆运算:
(1).1010 = ( )2 = ( )5
(2) x13·x7 =x( ) =( )5 =( )4 =( )10
(3)a2m =( )2 =( )m (m为正整数)
105
10220x4x5x2ama2填一填1、若 a5 . (an)3 = a11,则n= ,
2、若 2n+3 = 64,则n= ,
3、已知 644×83 = 2n,则n= 。2333(4)设n为正整数,且x2n=2,求9(x3n)2 的值。
已知10a=2,10b=3,求102a+3b的值。
解:∵ x2n=2
∴ 9(x3n)2 = 9(x2n)3 = 9×23=72思考探索(我相信你一定会成功)⑴ 22与32⑶ 340与 430哪个
大呢?⑵ 43与53想: 340=( )想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?底数不变指数相乘指数相加同底数幂相乘幂的乘方其中m , n都是正整数本节课的收获??相加相乘不变
不变任何成果的取得都需要
付出艰苦的劳动!
