2022-2023学年八年级下册数学 正比例函数 同步练习(含答案)
文档属性
| 名称 | 2022-2023学年八年级下册数学 正比例函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 322.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-08 20:27:08 | ||
图片预览


文档简介
2022-2023学年八年级下册数学 正比例函数 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列正比例函数中,y的值随x值的增大而减小是( )
A.y=8x B.y=0.6x C.yx D.y=()x
2.若函数是正比例函数,则m的值是( )
A.m=1 B.m=-2 C.m=2 D.m>-2
3.一个正比例函数的图象经过点,它的表达式为 ( )
A. B. C. D.
4.一次函数y=2x的图象经过的象限是( )
A.一、三 B.二、四 C.一、三、四 D.二、三、四
5.已知正比例函数,点、都在该函数图象上,则的值是( )
A.-2 B.-1 C.1 D.2
6.若、、三点都在函数的图像上,那么的大小关系是( )
A. B. C. D.
7.已知函数是关于的正比例函数,则关于字母、的取值正确的是( )
A., B., C., D.,
8.如果一个正比例函数的图象经过不同象限的两点A(3,m)、B(n,﹣2),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
9.已知4个正比例函数y=k1x,y=k2x,y=k3x,y=k4x的图像如图,则下列结论成立的是( )
A.k1>k2>k3>k4 B.k1>k2>k4>k3
C.k2>k1>k3>k4 D.k4>k3>k2>k1
10.如图,9个边长为1的正方形摆放在平面直角坐标系中,经过原点的直线l将九个正方形组成的图形面积分为1:2的两部分,则该直线的解析式为( )
A. B.
C.或 D.或
二、填空题(本大题共5小题,在横线上填上合理的答案)
11.(1)如果是y关于x的正比例函数,则k=_________.
(2)若是关于x的正比例函数,m=_________.
(3)如果y=3x+k-4是y关于x的正比例函数,则k=_____.
12.如果正比例函数y=(k﹣2)x的图象经过第二、四象限,那么k的取值范围是 _____.
13.若,则关于函数的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负值.正确的是________.(直接写出正确结论的序号)
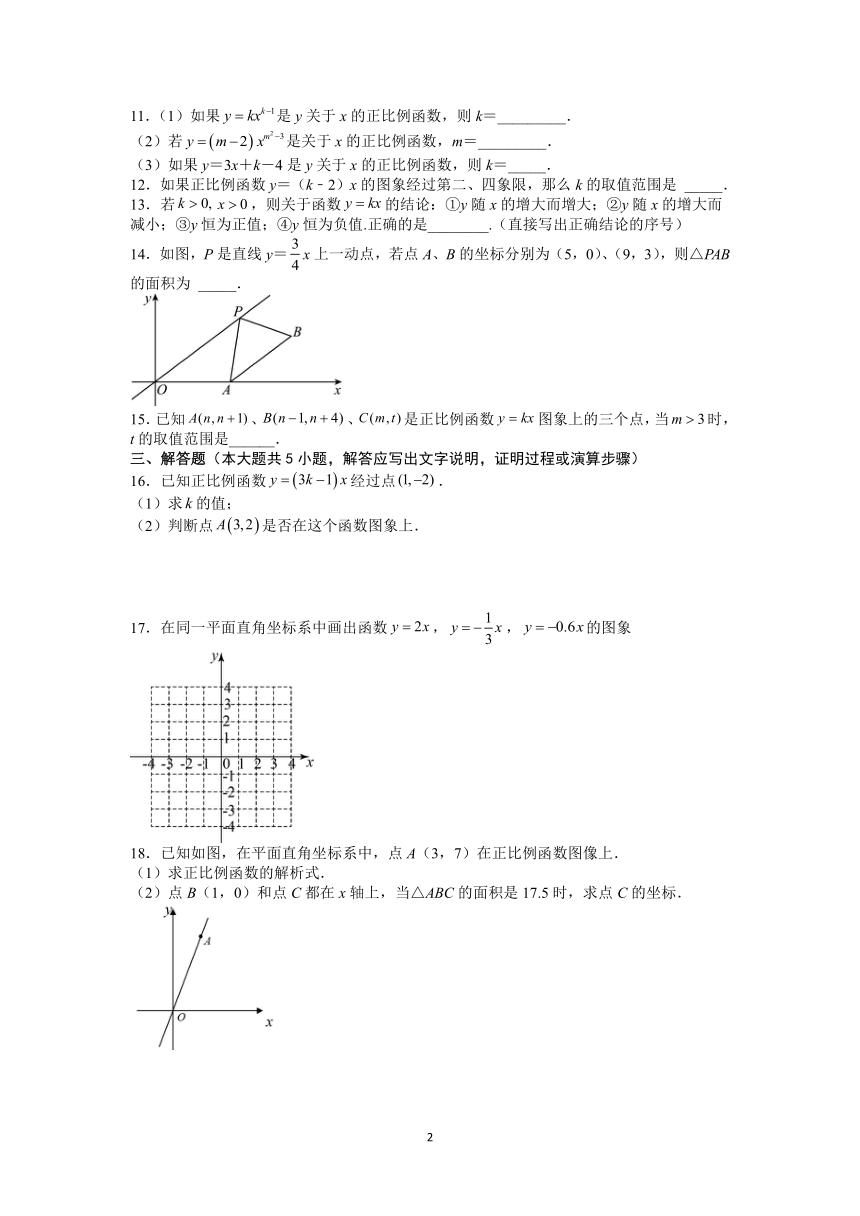
14.如图,P是直线y=x上一动点,若点A、B的坐标分别为(5,0)、(9,3),则△PAB的面积为 _____.
15.已知、、是正比例函数图象上的三个点,当时,t的取值范围是______.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
16.已知正比例函数经过点.
(1)求的值;
(2)判断点是否在这个函数图象上.
17.在同一平面直角坐标系中画出函数,,的图象
18.已知如图,在平面直角坐标系中,点A(3,7)在正比例函数图像上.
(1)求正比例函数的解析式.
(2)点B(1,0)和点C都在x轴上,当△ABC的面积是17.5时,求点C的坐标.
19.如图,已知正比例函数的表达式为y=﹣x,过正比例函数在第四象限图象上的一点A作x轴的垂线,交x轴于点H,AH=2,求线段OA的长.
20.已知y﹣3与2x﹣1成正比例,且当x=1时,y=6.
(1)求y与x之间的函数解析式.
(2)当x=2时,求y的值.
(3)若点A(x1,y1),B(x2,y2)都在该函数的图象上,且y1>y2,试判断x1,x2的大小关系.
21.如图,点A(1,4)在正比例函数的图象上,点B(3,n)在正比例函数的图象上.
(1)求m,n的值;
(2)在x轴找一点P,使得PA+PB的值最小,请求出PA+PB的最小值.
答案:
1.D 2.B 3.A 4.A 5.D 6.D 7.A 8.B 9.A 10.C 11. 2 -2 4
12. 13.①③ 14.. 15.
16.解:(1)因为点在正比例函数的图象上,
所以
所以
解得
(2)由(1)知,,
将代入得:.
所以点不在这个函数图象上.
17.解:列表:
0 1
0 2
0
0
描点、画图:
18.解:(1)设正比例函数的解析式为,
将点代入得:,解得,
则正比例函数的解析式为;
(2)如图,过点作轴于点,
,
,
设点的坐标为,则,
的面积是,
,即,
解得或,
故点的坐标为或.
19.解:∵AH⊥x轴,AH=2,点A在第四象限,
∴A点的纵坐标为﹣2,
代入得,解得x=4,
∴A(4,﹣2),
∴OH=4,
∴OA=.
19.解:(1)设y﹣3=k(2x﹣1),
把x=1,y=6代入得6﹣3=k(2×1﹣1),解得k=3,
则y﹣3=3(2x﹣1),
所以y与x之间的函数解析式为y=6x;
(2)由(1)知,y=6x
∴当x=2x时,y=6=12;
(3)∵,
而,
∴
∴
20.(1)解:∵点A(1,4)在正比例函数的图象上,点B(3,n)在正比例函数的图象上.
∴
∴.
(2)解:作点A(1,4)关于x轴对称的点,连接,交x轴于点P,此时PA+PB的值最小, PA+PB=.
过点作∥x轴,过点B作∥y轴,和相交于点H,
在Rt△中,∠H=90°,
则,
∴PA+PB的最小值为 .
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列正比例函数中,y的值随x值的增大而减小是( )
A.y=8x B.y=0.6x C.yx D.y=()x
2.若函数是正比例函数,则m的值是( )
A.m=1 B.m=-2 C.m=2 D.m>-2
3.一个正比例函数的图象经过点,它的表达式为 ( )
A. B. C. D.
4.一次函数y=2x的图象经过的象限是( )
A.一、三 B.二、四 C.一、三、四 D.二、三、四
5.已知正比例函数,点、都在该函数图象上,则的值是( )
A.-2 B.-1 C.1 D.2
6.若、、三点都在函数的图像上,那么的大小关系是( )
A. B. C. D.
7.已知函数是关于的正比例函数,则关于字母、的取值正确的是( )
A., B., C., D.,
8.如果一个正比例函数的图象经过不同象限的两点A(3,m)、B(n,﹣2),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
9.已知4个正比例函数y=k1x,y=k2x,y=k3x,y=k4x的图像如图,则下列结论成立的是( )
A.k1>k2>k3>k4 B.k1>k2>k4>k3
C.k2>k1>k3>k4 D.k4>k3>k2>k1
10.如图,9个边长为1的正方形摆放在平面直角坐标系中,经过原点的直线l将九个正方形组成的图形面积分为1:2的两部分,则该直线的解析式为( )
A. B.
C.或 D.或
二、填空题(本大题共5小题,在横线上填上合理的答案)
11.(1)如果是y关于x的正比例函数,则k=_________.
(2)若是关于x的正比例函数,m=_________.
(3)如果y=3x+k-4是y关于x的正比例函数,则k=_____.
12.如果正比例函数y=(k﹣2)x的图象经过第二、四象限,那么k的取值范围是 _____.
13.若,则关于函数的结论:①y随x的增大而增大;②y随x的增大而减小;③y恒为正值;④y恒为负值.正确的是________.(直接写出正确结论的序号)
14.如图,P是直线y=x上一动点,若点A、B的坐标分别为(5,0)、(9,3),则△PAB的面积为 _____.
15.已知、、是正比例函数图象上的三个点,当时,t的取值范围是______.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
16.已知正比例函数经过点.
(1)求的值;
(2)判断点是否在这个函数图象上.
17.在同一平面直角坐标系中画出函数,,的图象
18.已知如图,在平面直角坐标系中,点A(3,7)在正比例函数图像上.
(1)求正比例函数的解析式.
(2)点B(1,0)和点C都在x轴上,当△ABC的面积是17.5时,求点C的坐标.
19.如图,已知正比例函数的表达式为y=﹣x,过正比例函数在第四象限图象上的一点A作x轴的垂线,交x轴于点H,AH=2,求线段OA的长.
20.已知y﹣3与2x﹣1成正比例,且当x=1时,y=6.
(1)求y与x之间的函数解析式.
(2)当x=2时,求y的值.
(3)若点A(x1,y1),B(x2,y2)都在该函数的图象上,且y1>y2,试判断x1,x2的大小关系.
21.如图,点A(1,4)在正比例函数的图象上,点B(3,n)在正比例函数的图象上.
(1)求m,n的值;
(2)在x轴找一点P,使得PA+PB的值最小,请求出PA+PB的最小值.
答案:
1.D 2.B 3.A 4.A 5.D 6.D 7.A 8.B 9.A 10.C 11. 2 -2 4
12. 13.①③ 14.. 15.
16.解:(1)因为点在正比例函数的图象上,
所以
所以
解得
(2)由(1)知,,
将代入得:.
所以点不在这个函数图象上.
17.解:列表:
0 1
0 2
0
0
描点、画图:
18.解:(1)设正比例函数的解析式为,
将点代入得:,解得,
则正比例函数的解析式为;
(2)如图,过点作轴于点,
,
,
设点的坐标为,则,
的面积是,
,即,
解得或,
故点的坐标为或.
19.解:∵AH⊥x轴,AH=2,点A在第四象限,
∴A点的纵坐标为﹣2,
代入得,解得x=4,
∴A(4,﹣2),
∴OH=4,
∴OA=.
19.解:(1)设y﹣3=k(2x﹣1),
把x=1,y=6代入得6﹣3=k(2×1﹣1),解得k=3,
则y﹣3=3(2x﹣1),
所以y与x之间的函数解析式为y=6x;
(2)由(1)知,y=6x
∴当x=2x时,y=6=12;
(3)∵,
而,
∴
∴
20.(1)解:∵点A(1,4)在正比例函数的图象上,点B(3,n)在正比例函数的图象上.
∴
∴.
(2)解:作点A(1,4)关于x轴对称的点,连接,交x轴于点P,此时PA+PB的值最小, PA+PB=.
过点作∥x轴,过点B作∥y轴,和相交于点H,
在Rt△中,∠H=90°,
则,
∴PA+PB的最小值为 .
