18.1.1平行四边形性质(1)上课
文档属性
| 名称 | 18.1.1平行四边形性质(1)上课 |  | |
| 格式 | zip | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-19 13:00:05 | ||
图片预览





文档简介
课件26张PPT。交换一个苹果,各得一个苹果;
交换一种思想,各得两种思想。
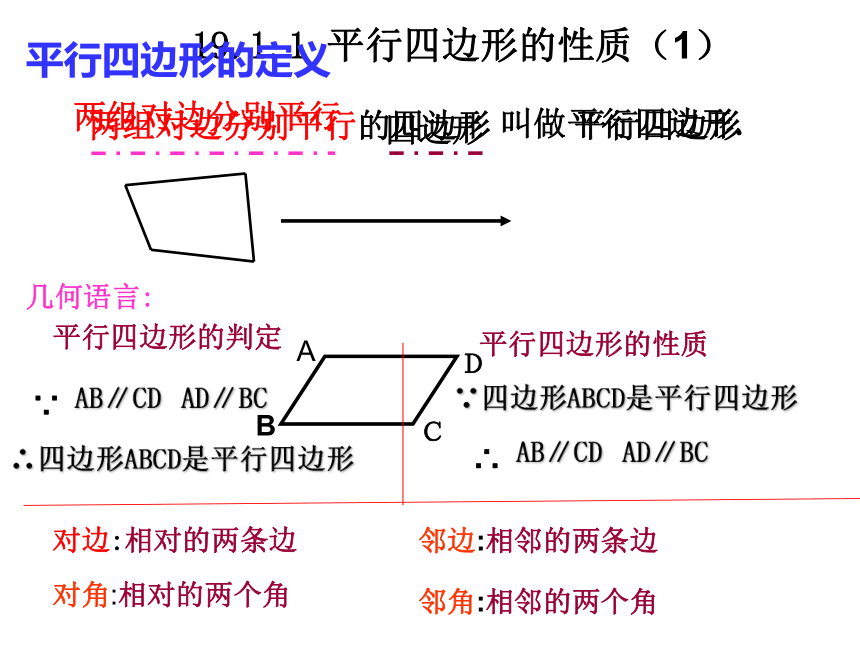
——萧伯纳四边形19.1.1 平行四边形的性质(1) 两组对边分别平行的四边形平行四边形的定义叫做平行四边形.两组对边分别平行平行四边形 几何语言:
对边:相对的两条边
邻边:相邻的两条边对角:相对的两个角邻角:相邻的两个角∴四边形ABCD是平行四边形∵四边形ABCD是平行四边形平行四边形的判定平行四边形的性质 (1)根据定义画一个平行四边形.
画一画 (2)度量这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间还有什么关系?
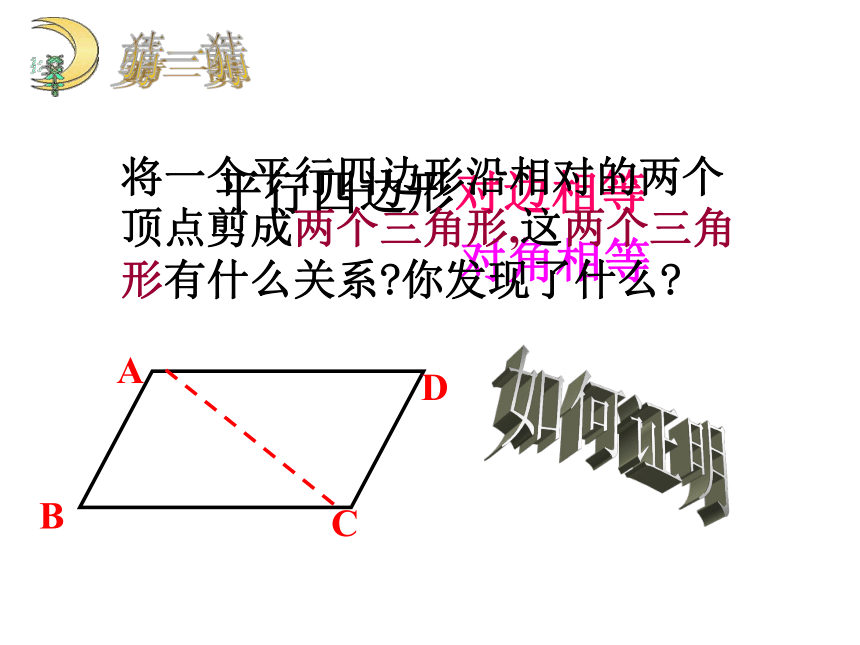
平行四边形对边相等 对角相等剪一剪将一个平行四边形沿相对的两个顶点剪成两个三角形,这两个三角形有什么关系?你发现了什么?
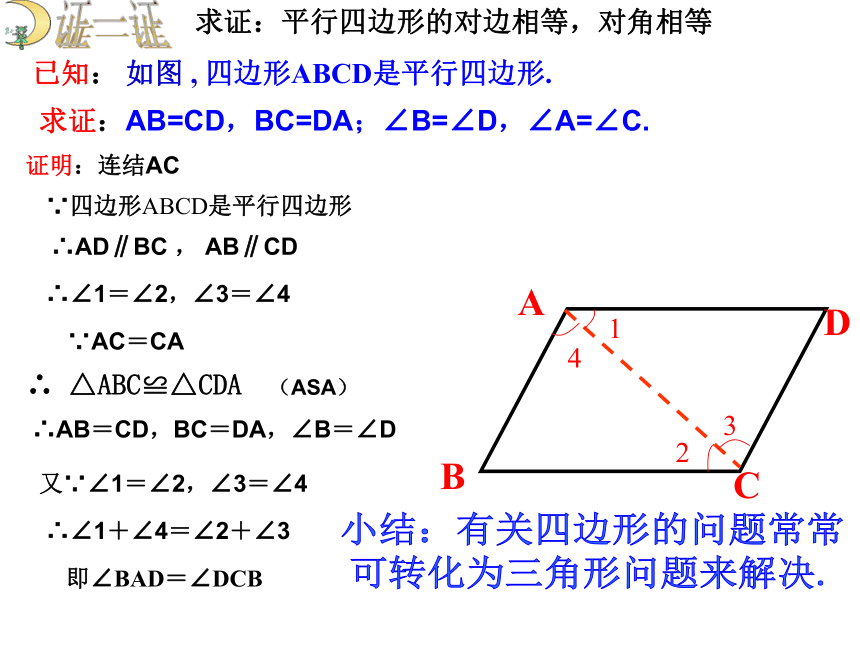
猜一猜如何证明已知: 如图 , 四边形ABCD是平行四边形.
即∠BAD=∠DCB证明:连结AC ∴AD∥BC , AB∥CD∴∠1=∠2,∠3=∠4 ∵AC=CA∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3求证:AB=CD,BC=DA;∠B=∠D,∠A=∠C.
求证:平行四边形的对边相等,对角相等(ASA)∵四边形ABCD是平行四边形小结:有关四边形的问题常常
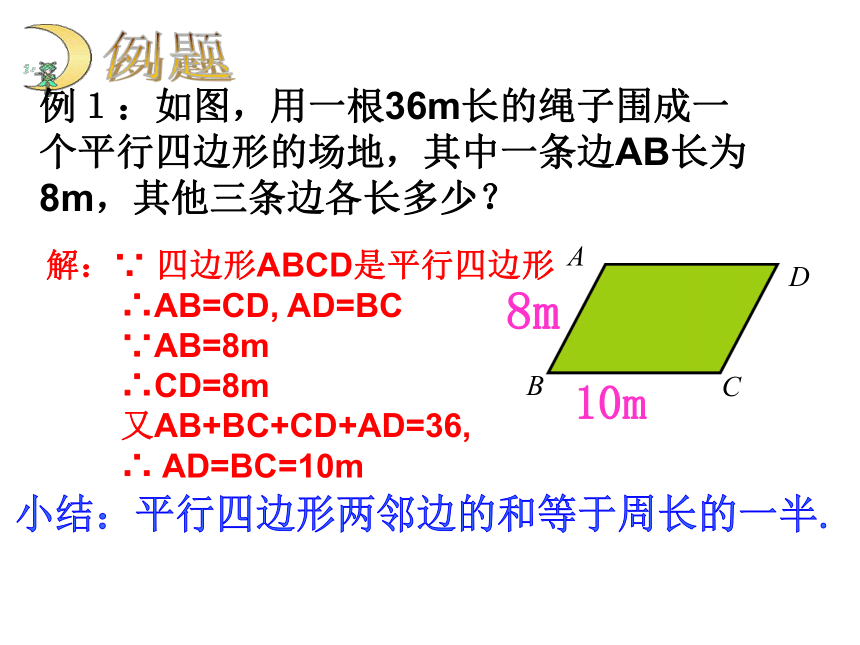
可转化为三角形问题来解决.∴ △ABC≌△CDA证一证小结:平行四边形两邻边的和等于周长的一半.例题例1:如图,用一根36m长的绳子围成一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?8m10m解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m 1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?32cm30cm56°124°124°小结:平行四边形中知道其中一角可求出另外三个角的度数,
知道其中两边可求出另外两边的长度。小试牛刀DE=BF 吗? 应用知识 解决问题 如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?猜 一 猜夹在两平行线间的平行线段相等。∟∟∟ 如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。平行线间的距离处处相等它与点与点的距离、点到直线的距离的联系与区别如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习练一练小结:平行四边形对角相等,邻角互补。3550°50°130°130°120°120°60°) 2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形.
(1)这是一个什么四边形?为什么?
线段AD和BC的长度有什么关系?α(2)若这个四边形的一个外角∠α=38°,
这个四边形的每个内角的
度数分别是多少?BACD练一练例2:如图: ABCD中,BE、DF分别平分∠ABC与∠ADC.求证: BE=DF.例题小结:利用平行四边形的性质可证明线段、角相等.如图: ABCD中,AE平分∠DAB,AB=5cm,AD=9cm,求EC的长度. 1CABDE25cm9cm练一练 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。边对边平行且相等;角对角相等,邻角互补.
平行四边形的性质:小结本节课我们学习了
①平行四边形的定义、性质:
边:平行四边形的对边平行且相等;
角:平行四边形的对角相等;邻角互补;
②方法:证明平行、线段相等、角相等的新方法;
③转化思想:四边形问题常转化为三角形问题解决。课堂小结 在数学的天地里,
重要的不是我们知道什么,
而是我们怎么知道什么.
今天我们经历
从“实验—猜想—证明”的过程,
探索并验证了平行四边形的性质.
在性质的证明和应用中,
我们体会到数学的严谨性,
感受到逻辑推理的严密性.
数学来源于生活,
也应用于生活.
未来的日子里,
希望同学们善于用数学的眼光,
去观察、思考、解决问题
……
作业:(1)作业本(2)课外作业:请你用平行四边形设计漂亮的图案. 欢迎大家来
二中做客!
交换一种思想,各得两种思想。
——萧伯纳四边形19.1.1 平行四边形的性质(1) 两组对边分别平行的四边形平行四边形的定义叫做平行四边形.两组对边分别平行平行四边形 几何语言:
对边:相对的两条边
邻边:相邻的两条边对角:相对的两个角邻角:相邻的两个角∴四边形ABCD是平行四边形∵四边形ABCD是平行四边形平行四边形的判定平行四边形的性质 (1)根据定义画一个平行四边形.
画一画 (2)度量这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间还有什么关系?
平行四边形对边相等 对角相等剪一剪将一个平行四边形沿相对的两个顶点剪成两个三角形,这两个三角形有什么关系?你发现了什么?
猜一猜如何证明已知: 如图 , 四边形ABCD是平行四边形.
即∠BAD=∠DCB证明:连结AC ∴AD∥BC , AB∥CD∴∠1=∠2,∠3=∠4 ∵AC=CA∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3求证:AB=CD,BC=DA;∠B=∠D,∠A=∠C.
求证:平行四边形的对边相等,对角相等(ASA)∵四边形ABCD是平行四边形小结:有关四边形的问题常常
可转化为三角形问题来解决.∴ △ABC≌△CDA证一证小结:平行四边形两邻边的和等于周长的一半.例题例1:如图,用一根36m长的绳子围成一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?8m10m解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m 1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?32cm30cm56°124°124°小结:平行四边形中知道其中一角可求出另外三个角的度数,
知道其中两边可求出另外两边的长度。小试牛刀DE=BF 吗? 应用知识 解决问题 如图,l1 // l2 , 线段AB//CD//EF, 且点A、C、E在l1上,B、D、F在l2上,则AB、CD、EF的长短相等吗?为什么?猜 一 猜夹在两平行线间的平行线段相等。∟∟∟ 如图,l1 // l2 ,点A、C、E在l1上,线段AB、CD、EF都垂直与l2 ,垂足分别为B、D、F,则AB、CD、EF的长短相等吗?为什么?一条直线上的任一点到另一条直线的距离,叫做这两条平行线间的距离。平行线间的距离处处相等它与点与点的距离、点到直线的距离的联系与区别如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习练一练小结:平行四边形对角相等,邻角互补。3550°50°130°130°120°120°60°) 2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形.
(1)这是一个什么四边形?为什么?
线段AD和BC的长度有什么关系?α(2)若这个四边形的一个外角∠α=38°,
这个四边形的每个内角的
度数分别是多少?BACD练一练例2:如图: ABCD中,BE、DF分别平分∠ABC与∠ADC.求证: BE=DF.例题小结:利用平行四边形的性质可证明线段、角相等.如图: ABCD中,AE平分∠DAB,AB=5cm,AD=9cm,求EC的长度. 1CABDE25cm9cm练一练 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。边对边平行且相等;角对角相等,邻角互补.
平行四边形的性质:小结本节课我们学习了
①平行四边形的定义、性质:
边:平行四边形的对边平行且相等;
角:平行四边形的对角相等;邻角互补;
②方法:证明平行、线段相等、角相等的新方法;
③转化思想:四边形问题常转化为三角形问题解决。课堂小结 在数学的天地里,
重要的不是我们知道什么,
而是我们怎么知道什么.
今天我们经历
从“实验—猜想—证明”的过程,
探索并验证了平行四边形的性质.
在性质的证明和应用中,
我们体会到数学的严谨性,
感受到逻辑推理的严密性.
数学来源于生活,
也应用于生活.
未来的日子里,
希望同学们善于用数学的眼光,
去观察、思考、解决问题
……
作业:(1)作业本(2)课外作业:请你用平行四边形设计漂亮的图案. 欢迎大家来
二中做客!
