18.1.2平行四边形的判定(2)上课
文档属性
| 名称 | 18.1.2平行四边形的判定(2)上课 |

|
|
| 格式 | zip | ||
| 文件大小 | 380.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-19 00:00:00 | ||
图片预览




文档简介
课件26张PPT。18.1.2平行四边形的判定(2)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形忆一忆平行四边形的判定方法 1、已知在四边形ABCD中,AD∥BC,要使这个四边形为平行四边形,则需添加一个你认为正确的条件为 ( ) A B∥DC,或∠A =∠C或AD=BC 2、能判定一个四边形是平行四边形的条件是( )A、一组对角相等 B、一组对边平行且相等
C、一对邻角互补 D、两条对角线互相垂直B3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )CA、AB = CD B、AD∥BC
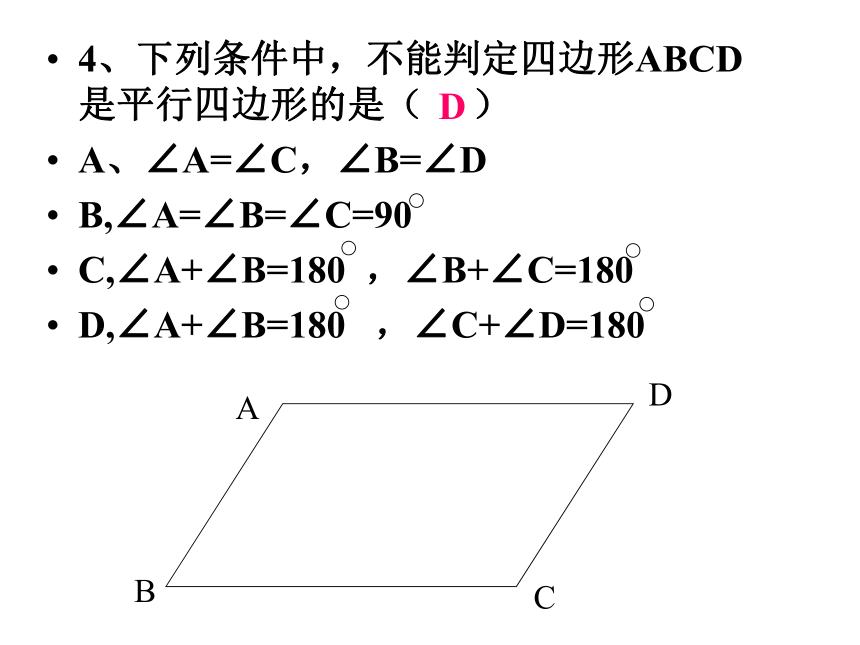
C、∠A = ∠B D、对角线互相平分练一练4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
B,∠A=∠B=∠C=90
C,∠A+∠B=180 ,∠B+∠C=180
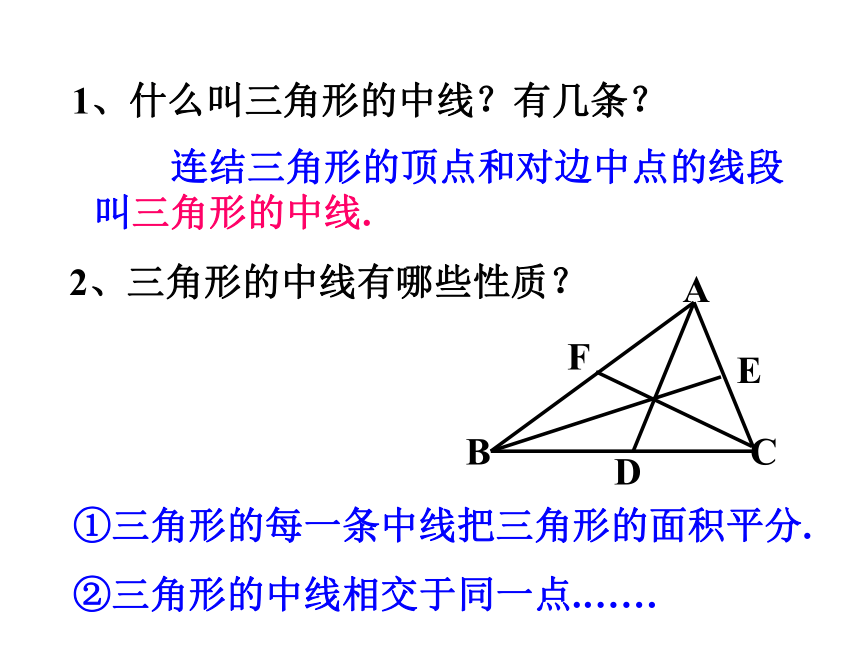
D,∠A+∠B=180 ,∠C+∠D=180D1、什么叫三角形的中线?有几条?2、三角形的中线有哪些性质?ABC 连结三角形的顶点和对边中点的线段叫三角形的中线.①三角形的每一条中线把三角形的面积平分.
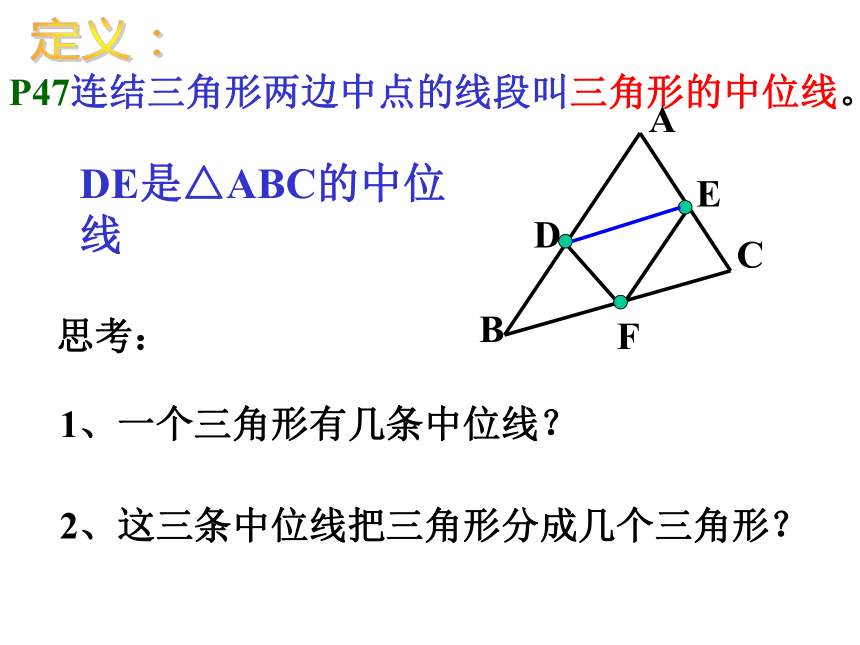
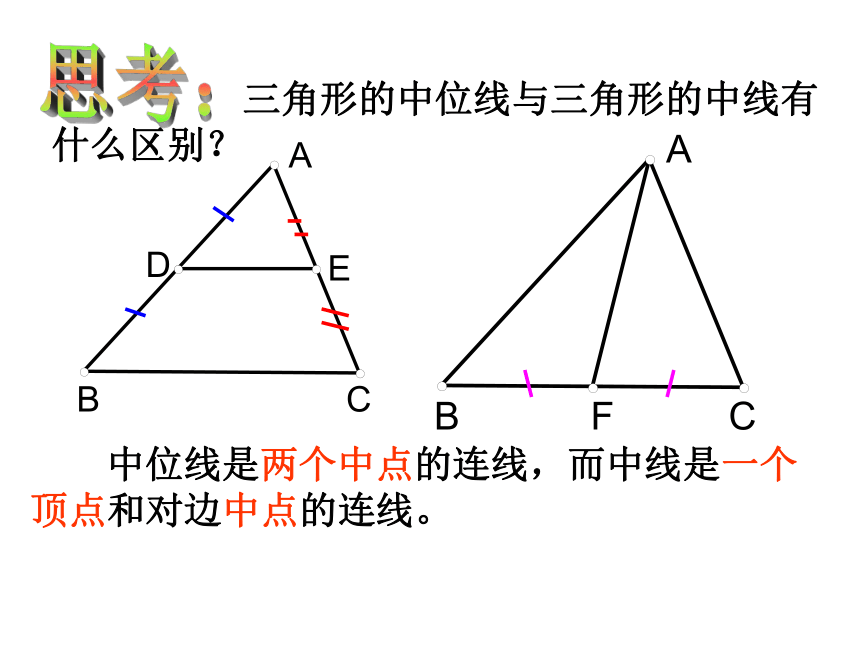
②三角形的中线相交于同一点.……EP47连结三角形两边中点的线段叫三角形的中位线。思考:1、一个三角形有几条中位线?2、这三条中位线把三角形分成几个三角形?DDE是△ABC的中位线定义: 三角形的中位线与三角形的中线有什么区别?思考: 中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。三角形的中位线具有怎样的性质呢?即DE与BC有什么样的
位置关系和数量关系?猜想:三角形的中位线平行于第三边,并且等于第三边的一半。如何证明?ABCDEF∵DE=EF ∠AED=∠CEF AE=EC
∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.∴AD=FC 、∠A=∠ECF
∴AB∥FC又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形还有另外的证法吗?∴DF∥BC,DF=BC又∵即DE∥BC 已知在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。 如图,点D、E分别是△ABC的边AB、AC的中点, 求证:DE∥BC且DE= BC证明:延长DE到F,使EF=DE,连接FC、DC、AF∴四边形ADCF是平行四边形∴四边形DBCF是平行四边形∵AE=EC∴ CF∥DA,CF=DA∴CF∥BD,CF=BDDF∥BC,DF=BC又DE= DF∴DE∥BC且DE= BC三角形的中位线的定理 三角形的中位线平行于第三边,并且等于它的一半巩固练习1.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你能在
图中画出多少个平行四边形?2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC应用:例1:口答
(1)三角形的周长为18cm,这个三角形的三条中位线围成三角形的周长是多少?为什么?(2)如图,E是平行四边形ABCD的AB边上的中点,且AD=10cm,那么OE= cm。5(3)如图:如果AD= AB,AE= AC,
DE=2cm,那么BC= cm。(4)在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。811 5.如图,四边形ABCD的对角线交于点O,下列判断若正确,请在括号里打上“√”号,若错误打上“×”号.⑴如果AB//DC,AD//BC,则四边形ABCD是平行四边形( )⑵如果∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形( )⑶如果OA=OC,OB=OD,则四边形ABCD是平行四边形( )⑷如果∠ABC与∠BAD互补,∠ABC与∠BCD互补,则四边形ABCD是平行四边形( )⑸如果∠ABD=∠BDC,∠ADB=∠DBC,则四边形ABCD是平行四边形( )√√√√√O练 习6.(常州)已知,四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件: ①AB∥CD;②OA=OC;③AB=CD; ④∠BAD=∠DCB;⑤AD∥BC. ⑵对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举出反例说明.⑴从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示);(能推出四边形ABCD是平行四边形的有①与②,
①与③,①与④,①与⑤,②与⑤,④与⑤, 不能推出四边形ABCD是平行四边形的有②与③,②与④,③与④, ③ 与⑤, )例2:如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,
求证:(1)∠A= ∠DEF
(2)四边形ADEF的周长等于AB+AC思考:(1)图中有几个平行四边形?(2)这四个三角形有什么关系?例3:已知,如图AD是△ABC的中线,EF是中位线,
求证:AD与EF互相平分例4:求证顺次连结四边形各边中点所得的四边形是平行四边形。已知:E、F、G、H分别是四边形ABCD中AB、
BC、CD、DA的中点。
求证:EFGH是平行四边形。任意四边形四边中点连线所得的四边形一定是平行四边形。例5:如图,任意四边形ABCD,E、F分别是AD、BC的中点,试说明EF与两条对角线AC、BD有什么关系。M任意四边形一组对边中点的连线段小于两条对角线和的一半。小结1、三角形中位线的定义2、三角形中位线定理连接三角形两边中点的线段叫做三角形的中位线三角形的中位线平行于三角形的第三边,且等于第三边的一半再见5,下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D例6:已知,四边形ABCD中,F是AB的点,E是CD的中点,
求证:EF (AD+BC)
C、一对邻角互补 D、两条对角线互相垂直B3、四边形ABCD中,若∠A = ∠C,∠B = ∠D,则下列结论中错误的是( )CA、AB = CD B、AD∥BC
C、∠A = ∠B D、对角线互相平分练一练4、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
B,∠A=∠B=∠C=90
C,∠A+∠B=180 ,∠B+∠C=180
D,∠A+∠B=180 ,∠C+∠D=180D1、什么叫三角形的中线?有几条?2、三角形的中线有哪些性质?ABC 连结三角形的顶点和对边中点的线段叫三角形的中线.①三角形的每一条中线把三角形的面积平分.
②三角形的中线相交于同一点.……EP47连结三角形两边中点的线段叫三角形的中位线。思考:1、一个三角形有几条中位线?2、这三条中位线把三角形分成几个三角形?DDE是△ABC的中位线定义: 三角形的中位线与三角形的中线有什么区别?思考: 中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。三角形的中位线具有怎样的性质呢?即DE与BC有什么样的
位置关系和数量关系?猜想:三角形的中位线平行于第三边,并且等于第三边的一半。如何证明?ABCDEF∵DE=EF ∠AED=∠CEF AE=EC
∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.∴AD=FC 、∠A=∠ECF
∴AB∥FC又AD=DB ∴BD∥ CF且 BD =CF
所以 ,四边形BCFD是平行四边形还有另外的证法吗?∴DF∥BC,DF=BC又∵即DE∥BC 已知在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。 如图,点D、E分别是△ABC的边AB、AC的中点, 求证:DE∥BC且DE= BC证明:延长DE到F,使EF=DE,连接FC、DC、AF∴四边形ADCF是平行四边形∴四边形DBCF是平行四边形∵AE=EC∴ CF∥DA,CF=DA∴CF∥BD,CF=BDDF∥BC,DF=BC又DE= DF∴DE∥BC且DE= BC三角形的中位线的定理 三角形的中位线平行于第三边,并且等于它的一半巩固练习1.如图,点D、E、F分别是△ABC的边AB、
BC、CA的中点,以这些点为顶点,你能在
图中画出多少个平行四边形?2.如图, A 、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点的实际距离?根据是什么?ABC应用:例1:口答
(1)三角形的周长为18cm,这个三角形的三条中位线围成三角形的周长是多少?为什么?(2)如图,E是平行四边形ABCD的AB边上的中点,且AD=10cm,那么OE= cm。5(3)如图:如果AD= AB,AE= AC,
DE=2cm,那么BC= cm。(4)在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是 。811 5.如图,四边形ABCD的对角线交于点O,下列判断若正确,请在括号里打上“√”号,若错误打上“×”号.⑴如果AB//DC,AD//BC,则四边形ABCD是平行四边形( )⑵如果∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形( )⑶如果OA=OC,OB=OD,则四边形ABCD是平行四边形( )⑷如果∠ABC与∠BAD互补,∠ABC与∠BCD互补,则四边形ABCD是平行四边形( )⑸如果∠ABD=∠BDC,∠ADB=∠DBC,则四边形ABCD是平行四边形( )√√√√√O练 习6.(常州)已知,四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件: ①AB∥CD;②OA=OC;③AB=CD; ④∠BAD=∠DCB;⑤AD∥BC. ⑵对由以上5个条件中任意选取2个条件,不能推出四边形ABCD是平行四边形的,请选取一种情形举出反例说明.⑴从以上5个条件中任意选取2个条件,能推出四边形ABCD是平行四边形的有(用序号表示);(能推出四边形ABCD是平行四边形的有①与②,
①与③,①与④,①与⑤,②与⑤,④与⑤, 不能推出四边形ABCD是平行四边形的有②与③,②与④,③与④, ③ 与⑤, )例2:如图,点D、E、F分别是△ABC的边AB、BC、CA的中点,
求证:(1)∠A= ∠DEF
(2)四边形ADEF的周长等于AB+AC思考:(1)图中有几个平行四边形?(2)这四个三角形有什么关系?例3:已知,如图AD是△ABC的中线,EF是中位线,
求证:AD与EF互相平分例4:求证顺次连结四边形各边中点所得的四边形是平行四边形。已知:E、F、G、H分别是四边形ABCD中AB、
BC、CD、DA的中点。
求证:EFGH是平行四边形。任意四边形四边中点连线所得的四边形一定是平行四边形。例5:如图,任意四边形ABCD,E、F分别是AD、BC的中点,试说明EF与两条对角线AC、BD有什么关系。M任意四边形一组对边中点的连线段小于两条对角线和的一半。小结1、三角形中位线的定义2、三角形中位线定理连接三角形两边中点的线段叫做三角形的中位线三角形的中位线平行于三角形的第三边,且等于第三边的一半再见5,下列条件中能判定一个四边形是平行四边形的条件是( )
①一组对边相等,且一组对角相等,②一组对边相等且一条对角线平分另一条对角线,③一组对角相等,且这一组对角的顶点所连结的对角线被另一条对角线平分,④一组对角相等,且这一组对角的顶点所连结的对角线平分这组对角。
A、①和② B、②和③
C、②和④ D、只有④D例6:已知,四边形ABCD中,F是AB的点,E是CD的中点,
求证:EF (AD+BC)
