18.2.3 正方形 巩固练习 2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 18.2.3 正方形 巩固练习 2022-2023学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 256.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-08 20:46:03 | ||
图片预览

文档简介
18.2.3 正方形 巩固练习
一、单选题
1.如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
A.﹣4+4 B.4+4 C.8﹣4 D.+1
2.如图,在正方形 ABCD 内一点 E 连接BE,CE,过 C 作 CF⊥CE 与 BE 延长线交于点 F,连接 DF,DE.CE=CF=1,DE=,下列结论中:① ;② BF⊥DF;③点 D 到 CF 的距离为 2;④ .其中正确结论的个数是 ( )
A.1 B. 2 C. 3 D. 4
3.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC等于( )
A.45° B.55° C.60° D.75°
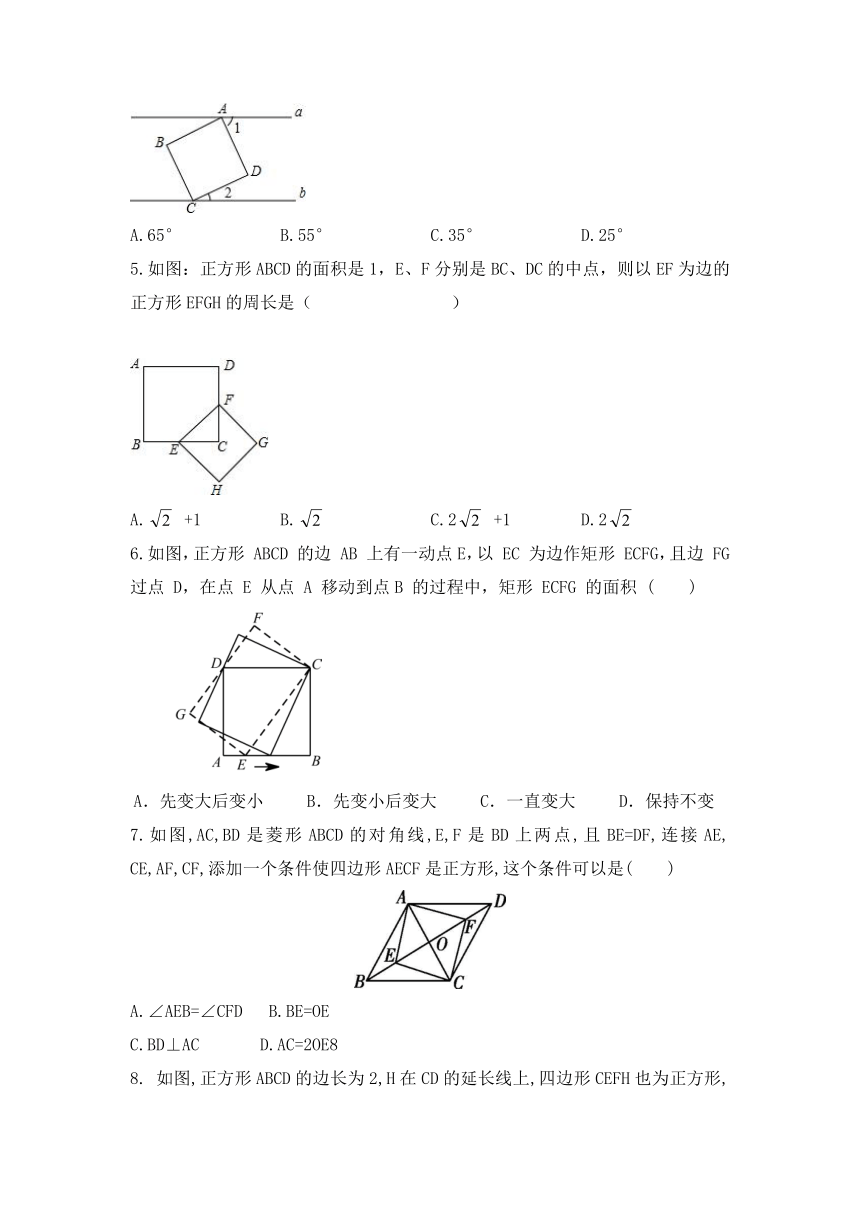
4、如图,正方形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=65°,则∠2的度数为( )
A.65° B.55° C.35° D.25°
5.如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
A. +1 B. C.2 +1 D.2
6.如图,正方形 ABCD 的边 AB 上有一动点E,以 EC 为边作矩形 ECFG,且边 FG 过点 D,在点 E 从点 A 移动到点B 的过程中,矩形 ECFG 的面积 ( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
7.如图,AC,BD是菱形ABCD的对角线,E,F是BD上两点,且BE=DF,连接AE, CE,AF,CF,添加一个条件使四边形AECF是正方形,这个条件可以是( )
A.∠AEB=∠CFD B.BE=OE
C.BD⊥AC D.AC=2OE8
8. 如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )
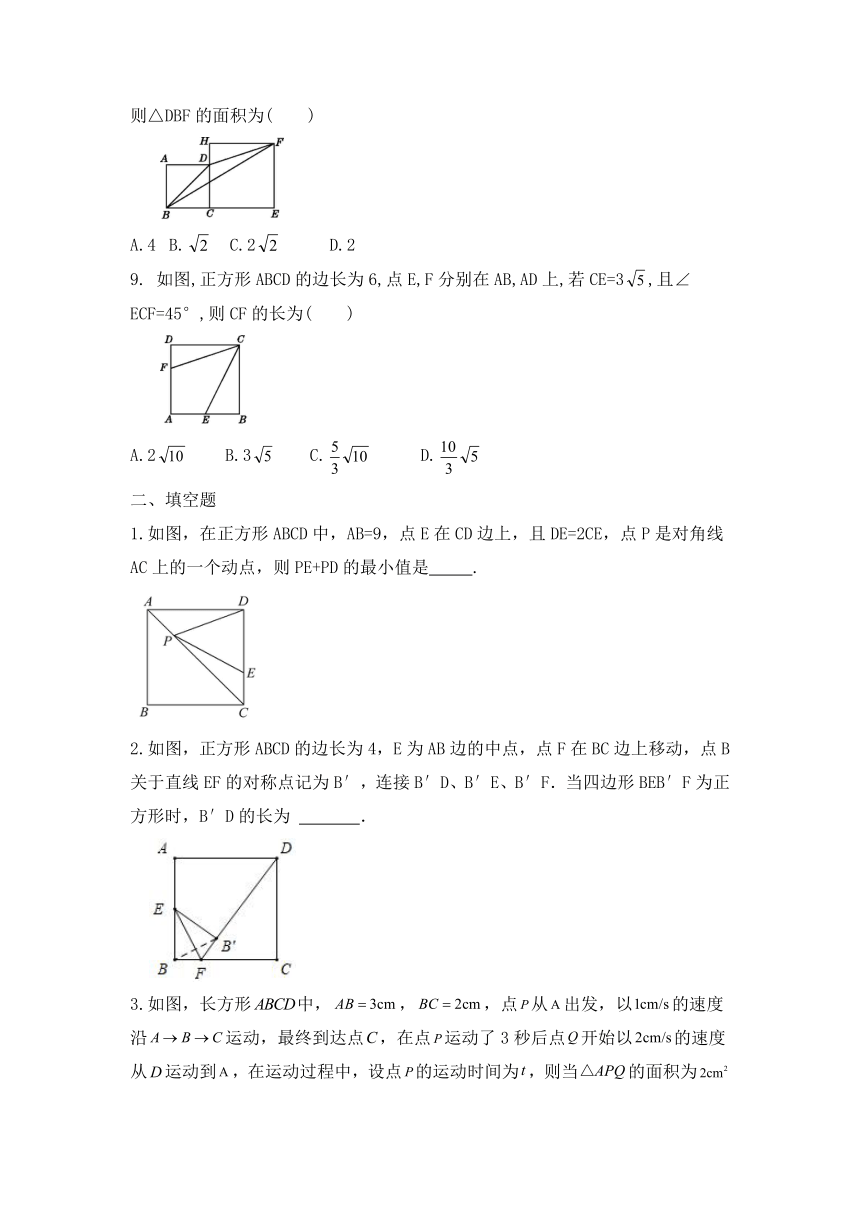
A.4 B. C.2 D.2
9. 如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为( )
A.2 B.3 C. D.
填空题
1.如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是 .
2.如图,正方形ABCD的边长为4,E为AB边的中点,点F在BC边上移动,点B关于直线EF的对称点记为B′,连接B′D、B′E、B′F.当四边形BEB′F为正方形时,B′D的长为 .
3.如图,长方形中,,,点从出发,以的速度沿运动,最终到达点,在点运动了3秒后点开始以的速度从运动到,在运动过程中,设点的运动时间为,则当的面积为时,的值为________.
4.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为______.
5.如图,在菱形中,,,点,同时由,两点出发,分别沿,方向向点匀速运动,点的运动速度为,点的运动速度为,点到达点后,点与点同时停止运动.若运动时间为秒时,为等边三角形,则的值为__________.
解答题
1.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段
BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB∶AD= 时,四边形MENF是正方形,并说明理由.
2.如图,在正方形ABCD的外侧作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE;
(2)求∠BEC的度数.
3.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
4.已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
5.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
6.已知:四边形ABCD是正方形,,点E,F,G,H分别在边AB,BC,AD,DC上.
(1)如图1,若,,则的度数为________;
(2)如图2,若,点E,F分别是AB,BC上的动点,求的周长;
(3)如图3,若,GF和EH交于点O,且,求EH的长度。
一、单选题
1.如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
A.﹣4+4 B.4+4 C.8﹣4 D.+1
2.如图,在正方形 ABCD 内一点 E 连接BE,CE,过 C 作 CF⊥CE 与 BE 延长线交于点 F,连接 DF,DE.CE=CF=1,DE=,下列结论中:① ;② BF⊥DF;③点 D 到 CF 的距离为 2;④ .其中正确结论的个数是 ( )
A.1 B. 2 C. 3 D. 4
3.如图,在正方形ABCD的外侧作等边三角形ADE,AC,BE相交于点F,则∠BFC等于( )
A.45° B.55° C.60° D.75°
4、如图,正方形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=65°,则∠2的度数为( )
A.65° B.55° C.35° D.25°
5.如图:正方形ABCD的面积是1,E、F分别是BC、DC的中点,则以EF为边的正方形EFGH的周长是( )
A. +1 B. C.2 +1 D.2
6.如图,正方形 ABCD 的边 AB 上有一动点E,以 EC 为边作矩形 ECFG,且边 FG 过点 D,在点 E 从点 A 移动到点B 的过程中,矩形 ECFG 的面积 ( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
7.如图,AC,BD是菱形ABCD的对角线,E,F是BD上两点,且BE=DF,连接AE, CE,AF,CF,添加一个条件使四边形AECF是正方形,这个条件可以是( )
A.∠AEB=∠CFD B.BE=OE
C.BD⊥AC D.AC=2OE8
8. 如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为( )
A.4 B. C.2 D.2
9. 如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为( )
A.2 B.3 C. D.
填空题
1.如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是 .
2.如图,正方形ABCD的边长为4,E为AB边的中点,点F在BC边上移动,点B关于直线EF的对称点记为B′,连接B′D、B′E、B′F.当四边形BEB′F为正方形时,B′D的长为 .
3.如图,长方形中,,,点从出发,以的速度沿运动,最终到达点,在点运动了3秒后点开始以的速度从运动到,在运动过程中,设点的运动时间为,则当的面积为时,的值为________.
4.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为______.
5.如图,在菱形中,,,点,同时由,两点出发,分别沿,方向向点匀速运动,点的运动速度为,点的运动速度为,点到达点后,点与点同时停止运动.若运动时间为秒时,为等边三角形,则的值为__________.
解答题
1.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段
BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB∶AD= 时,四边形MENF是正方形,并说明理由.
2.如图,在正方形ABCD的外侧作等边三角形ADE,连接BE,CE.
(1)求证:BE=CE;
(2)求∠BEC的度数.
3.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.
(1)求证:四边形MANP是正方形;
(2)求证:EM=BN.
4.已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
5.如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
6.已知:四边形ABCD是正方形,,点E,F,G,H分别在边AB,BC,AD,DC上.
(1)如图1,若,,则的度数为________;
(2)如图2,若,点E,F分别是AB,BC上的动点,求的周长;
(3)如图3,若,GF和EH交于点O,且,求EH的长度。
