人教版八年级下册18.2.3 正方形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.3 正方形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
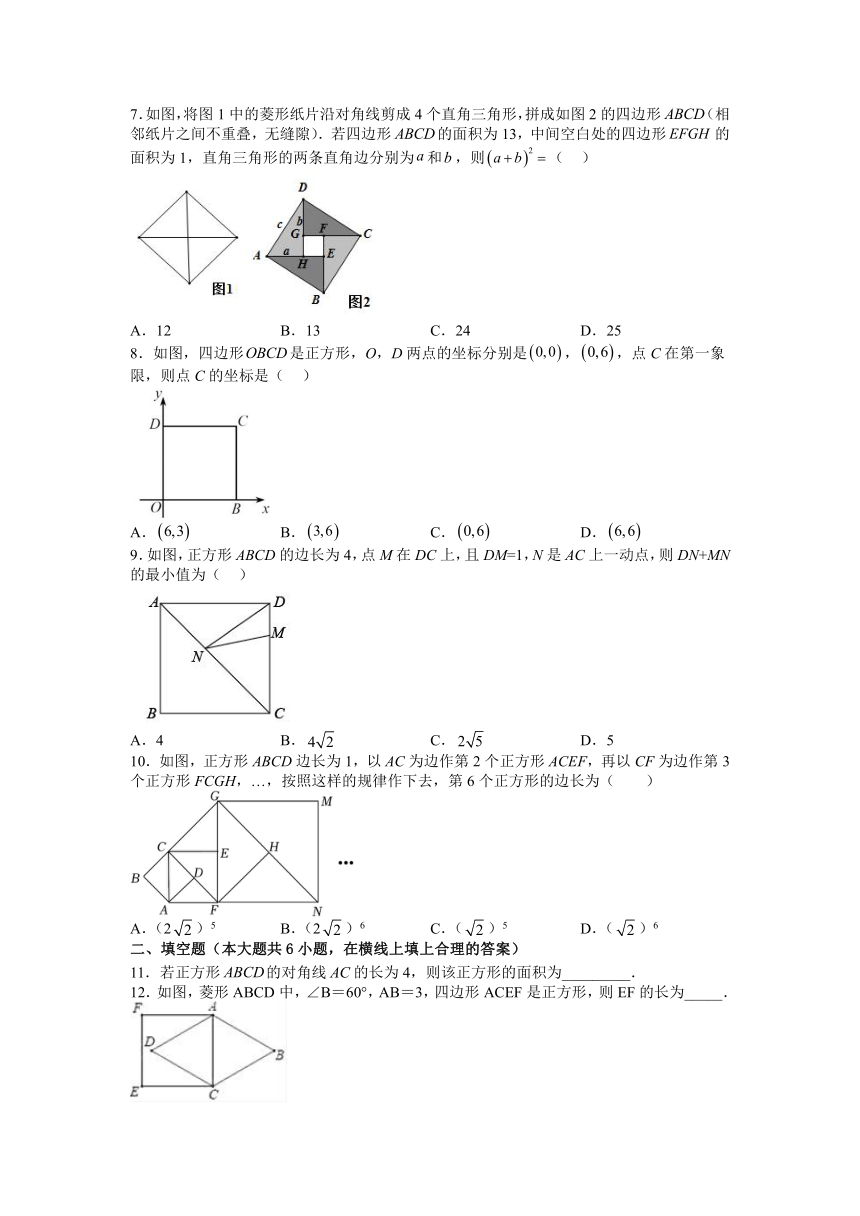
| 科目 | 数学 | ||
| 更新时间 | 2023-04-08 21:08:42 | ||
图片预览

文档简介
18.2.3 正方形 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线长度相等 D.一组对角线平分一组对角
2.如图,正方形ABCD的边长为7,在各边上顺次截取,则四边形EFGH的面积为( ).
A.20 B.25 C.30 D.35
3.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为( )
A.cm B.cm C.8cm D.10cm
4.如图,在菱形中,对角线,相交于点,只需添加一个条件,即可证明菱形是正方形,这个条件可以是( )
A. B. C. D.
5.如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB等于( ).
A.22.5° B.45° C.30° D.135°
6.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
7.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
8.如图,四边形是正方形,O,D两点的坐标分别是,,点C在第一象限,则点C的坐标是( )
A. B. C. D.
9.如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( )
A.4 B. C. D.5
10.如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A.(2)5 B.(2)6 C.()5 D.()6
二、填空题(本大题共6小题,在横线上填上合理的答案)
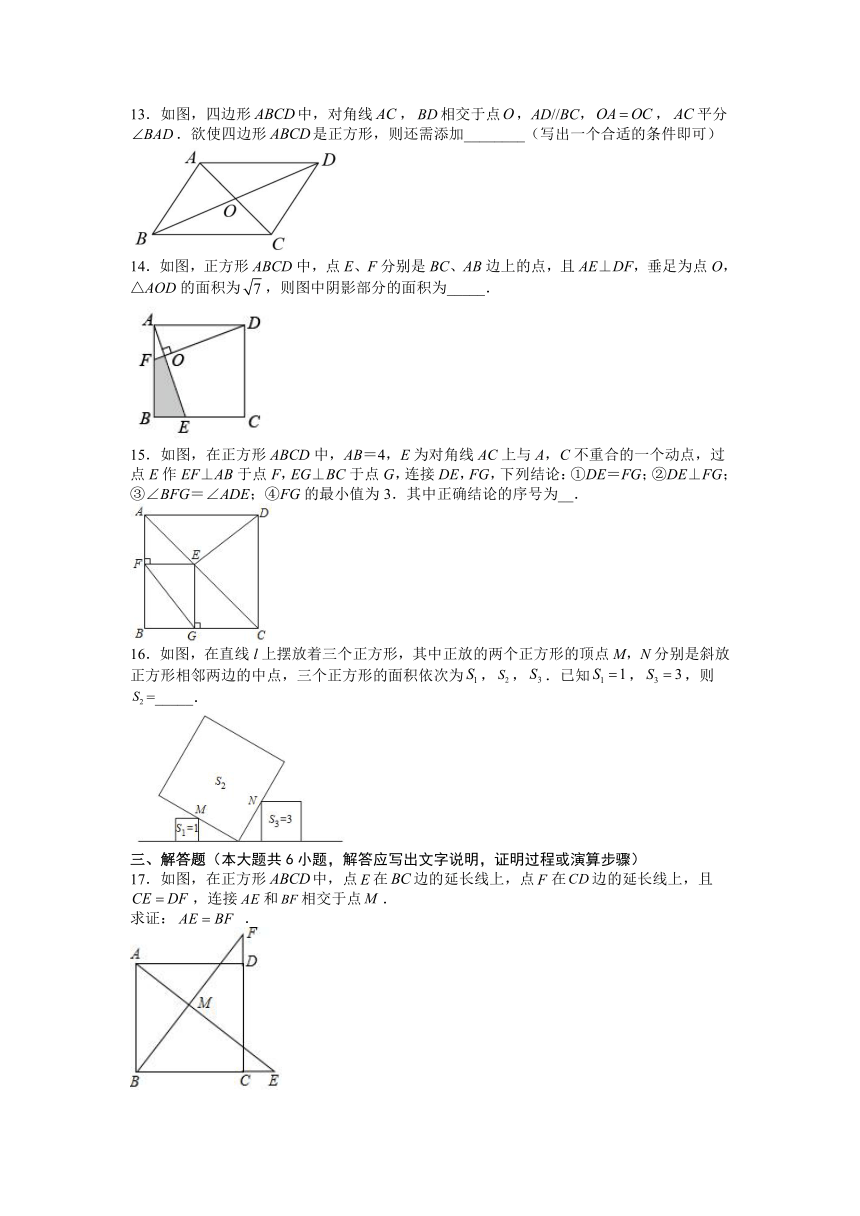
11.若正方形的对角线的长为4,则该正方形的面积为_________.
12.如图,菱形ABCD中,∠B=60°,AB=3,四边形ACEF是正方形,则EF的长为_____.
13.如图,四边形中,对角线,相交于点,AD//BC,,平分.欲使四边形是正方形,则还需添加________(写出一个合适的条件即可)
14.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
15.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的序号为__.
16.如图,在直线l上摆放着三个正方形,其中正放的两个正方形的顶点M,N分别是斜放正方形相邻两边的中点,三个正方形的面积依次为,,.已知,,则=_____.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
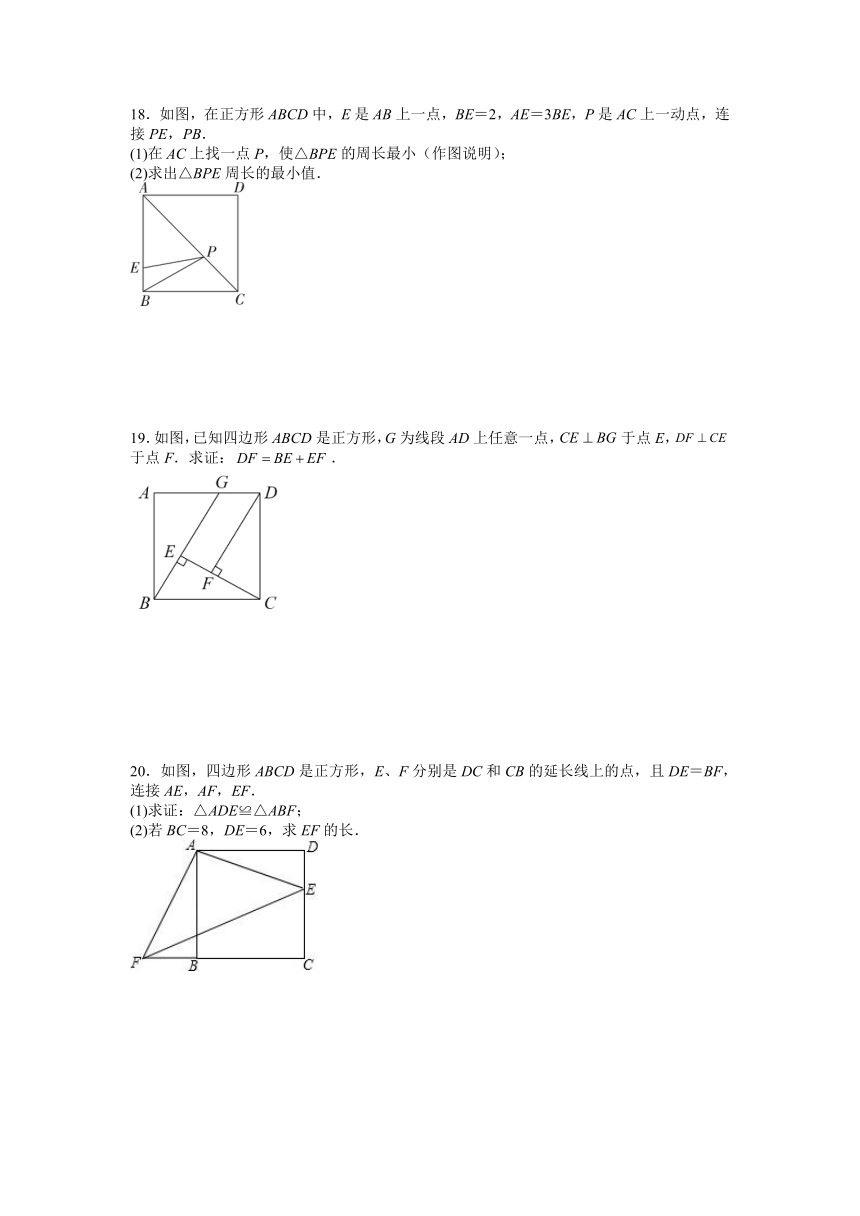
17.如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.
求证: .
18.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.
(1)在AC上找一点P,使△BPE的周长最小(作图说明);
(2)求出△BPE周长的最小值.
19.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
20.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
21.如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
22.由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示.
根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论∶若a>0,b>0且a2+b2为定值,则当a ____ b 时,ab取得最大值.
拓展: 如图所示,在正方形的四边上分别取点,使得,
(1)求证:四边形是正方形.
(2)若,求证四边形是正方形.
答案:
1.C 2.B 3.B 4.A 5.A 6.C 7.D 8.D 9.D 10.C 11.8
13.(答案不唯一) 14. 15.①②③ 16.16
17.证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°,
又∵CE=DF,
∴CE+BC=DF+CD即BE=CF,
在△BCF和△ABE中,
∴(SAS),
∴AE=BF.
18.(1)解:如图,连接DE,交AC于点P′,连接BP′,当点P在点P′处时,△BPE的周长最小.
理由:在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵AP′=AP′,
∴△ABP′≌△ADP′,
∴BP′=DP′,
∴BP+PE= DP′+ P′E≥DE,
即当点P位于PP′时,△BPE的周长PB+EP+BE最小;
(2)
解:由(1)得:B P′=DP′,
∴P′B+P′E=DE.
∵BE=2,AE=3BE,
∴AE=6.
∴AD=AB=8.
∴DE==10.
∴PB+PE的最小值是10.
∴△BPE周长的最小值为10+BE=10+2=12.
19.证明:四边形是正方形,
,
,
,
,
,
,
在和中,,
,
,
,
.
20.(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,AD=AB
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8﹣6=2,CF=8+6=14,
在Rt△FCE中,EF===10.
21.(1)由折叠性质知:∠BAE=∠EAG,∠DAF=∠FAG,
∵∠EAF=45°,
∴∠BAD=2∠EAF=245°=90°,
又∵∠B=∠D=90°,
∴四边形ABCD是矩形,
由折叠性质知:AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)∵EC=FC=1,
∴BE=DF,EF=,
∵EF=EG+GF=BE+DF,
∴BE=DF=EF=,
∴AB=BC=BE+EC=.
22.∵由“赵爽弦图”知,大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和,
即,
∴,
∴当a=b时,ab取得最大值,且最大值为;
故答案为:=;
拓展:
(1)在正方形中,,
,
又,
,
.
,
,
,
四边形是正方形.
(2),且,
四边形、四边形、四边形、四边形均为长方形,
,
,
,且,
四边形为正方形.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列性质中,矩形具有、正方形也具有、但是菱形却不具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线长度相等 D.一组对角线平分一组对角
2.如图,正方形ABCD的边长为7,在各边上顺次截取,则四边形EFGH的面积为( ).
A.20 B.25 C.30 D.35
3.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为( )
A.cm B.cm C.8cm D.10cm
4.如图,在菱形中,对角线,相交于点,只需添加一个条件,即可证明菱形是正方形,这个条件可以是( )
A. B. C. D.
5.如图,正方形ABCD中,以对角线AC为一边作菱形AEFC,则∠FAB等于( ).
A.22.5° B.45° C.30° D.135°
6.如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
7.如图,将图1中的菱形纸片沿对角线剪成4个直角三角形,拼成如图2的四边形(相邻纸片之间不重叠,无缝隙).若四边形的面积为13,中间空白处的四边形的面积为1,直角三角形的两条直角边分别为和,则( )
A.12 B.13 C.24 D.25
8.如图,四边形是正方形,O,D两点的坐标分别是,,点C在第一象限,则点C的坐标是( )
A. B. C. D.
9.如图,正方形ABCD的边长为4,点M在DC上,且DM=1,N是AC上一动点,则DN+MN的最小值为( )
A.4 B. C. D.5
10.如图,正方形ABCD边长为1,以AC为边作第2个正方形ACEF,再以CF为边作第3个正方形FCGH,…,按照这样的规律作下去,第6个正方形的边长为( )
A.(2)5 B.(2)6 C.()5 D.()6
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若正方形的对角线的长为4,则该正方形的面积为_________.
12.如图,菱形ABCD中,∠B=60°,AB=3,四边形ACEF是正方形,则EF的长为_____.
13.如图,四边形中,对角线,相交于点,AD//BC,,平分.欲使四边形是正方形,则还需添加________(写出一个合适的条件即可)
14.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
15.如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的序号为__.
16.如图,在直线l上摆放着三个正方形,其中正放的两个正方形的顶点M,N分别是斜放正方形相邻两边的中点,三个正方形的面积依次为,,.已知,,则=_____.
三、解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
17.如图,在正方形中,点在边的延长线上,点在边的延长线上,且,连接和相交于点.
求证: .
18.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.
(1)在AC上找一点P,使△BPE的周长最小(作图说明);
(2)求出△BPE周长的最小值.
19.如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
20.如图,四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
21.如图,在四边形纸片 ABCD 中,∠B=∠D=90°,点 E,F 分别在边 BC,CD 上,将 AB,AD 分别沿 AE,AF 折叠,点 B,D 恰好都和点 G 重合,∠EAF=45°.
(1)求证:四边形 ABCD 是正方形;
(2)若 EC=FC=1,求 AB 的长度.
22.由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示.
根据大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和证明了勾股定理a2+b2=c2,还可以用来证明结论∶若a>0,b>0且a2+b2为定值,则当a ____ b 时,ab取得最大值.
拓展: 如图所示,在正方形的四边上分别取点,使得,
(1)求证:四边形是正方形.
(2)若,求证四边形是正方形.
答案:
1.C 2.B 3.B 4.A 5.A 6.C 7.D 8.D 9.D 10.C 11.8
13.(答案不唯一) 14. 15.①②③ 16.16
17.证明:∵四边形ABCD为正方形,
∴AB=BC=CD,∠ABE=∠BCF=90°,
又∵CE=DF,
∴CE+BC=DF+CD即BE=CF,
在△BCF和△ABE中,
∴(SAS),
∴AE=BF.
18.(1)解:如图,连接DE,交AC于点P′,连接BP′,当点P在点P′处时,△BPE的周长最小.
理由:在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵AP′=AP′,
∴△ABP′≌△ADP′,
∴BP′=DP′,
∴BP+PE= DP′+ P′E≥DE,
即当点P位于PP′时,△BPE的周长PB+EP+BE最小;
(2)
解:由(1)得:B P′=DP′,
∴P′B+P′E=DE.
∵BE=2,AE=3BE,
∴AE=6.
∴AD=AB=8.
∴DE==10.
∴PB+PE的最小值是10.
∴△BPE周长的最小值为10+BE=10+2=12.
19.证明:四边形是正方形,
,
,
,
,
,
,
在和中,,
,
,
,
.
20.(1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,AD=AB
在△ADE和△ABF中,
,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8﹣6=2,CF=8+6=14,
在Rt△FCE中,EF===10.
21.(1)由折叠性质知:∠BAE=∠EAG,∠DAF=∠FAG,
∵∠EAF=45°,
∴∠BAD=2∠EAF=245°=90°,
又∵∠B=∠D=90°,
∴四边形ABCD是矩形,
由折叠性质知:AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)∵EC=FC=1,
∴BE=DF,EF=,
∵EF=EG+GF=BE+DF,
∴BE=DF=EF=,
∴AB=BC=BE+EC=.
22.∵由“赵爽弦图”知,大正方形的面积c2等于小正方形的面积(a-b)2与4个直角三角形的面积2ab的和,
即,
∴,
∴当a=b时,ab取得最大值,且最大值为;
故答案为:=;
拓展:
(1)在正方形中,,
,
又,
,
.
,
,
,
四边形是正方形.
(2),且,
四边形、四边形、四边形、四边形均为长方形,
,
,
,且,
四边形为正方形.
