第6单元正比例和反比例检测卷(单元测试)-小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元正比例和反比例检测卷(单元测试)-小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 08:32:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.下面四句话中不正确的一句是( )。
A.比的前项乘0.5,比的后项除以2,比值不变
B.100克含盐率为10%的盐水中加入5克盐,含盐达到15%
C.圆柱体的侧面积一定,则它的高和底面半径成反比例
D.一幅图的比例尺为100∶1,表示图上距离是实际距离的100倍
2.下面每组的两个量中,成正比例关系的是( )。
A.长方形的面积一定,长和宽 B.一个人的年龄和头发长度
C.时间一定,路程和速度 D.男生人数一定,女生人数和全班人数
3.根据下面的图像可以知道,图上距离和实际距离( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
4.下面说法不正确的是( )。
A.订阅《小学生数学报》的人数与总钱数成正比例。
B.同一时间,物体的高度和影长成正比例。
C.长方形的周长一定,长和宽成反比例。
D.给一个房间地面铺砖,每块砖的面积和铺砖的块数成反比例。
5.下列说法正确的是( )。
A.若,则与成反比例
B.若,则和成正比例
C.在一个比例中,若交换一个比的前项和后项的位置,则比例关系仍成立
D.在一个比例中,若交换两个外项或两个内项的位置,则比例关系仍成立
6.每页书的字数一定,书的页数和书的总字数( )。
A.成正比例关系 B.成反比例关系 C.不成比例关系 D.无法判断
二、填空题
7.圆的周长与它的( )成正比例;如果6÷x=y,那么x与y成( )比例。
8.A、B是两个非零自然数,如果A=B,那么A和B的最小公倍数是( ),A和B成( )比例。
9.某市出租公司有这样的规定,起步价4元(2公里之内),超过2公里而在5公里之内(含5公里),每公里按1.5元计价,5公里以上部分每公里再加价。
坐车的路程公里 应付的钱数元
2 ( )
5 ( )
6 ( )
从上表中你发现有( )和( )两种相关联的量,它们之间是( )比例关系。
10.下表中与两个量成反比例关系,请把表格填完整。
2 0.1 ( ) ( )
5 ( ) 2.5 ( )
11.图中,若与成正比例,则“?”是( )。
10 ?
8 4
12.、B、C三量的关系式A×B=C中,当C一定时,A和B成( )关系。
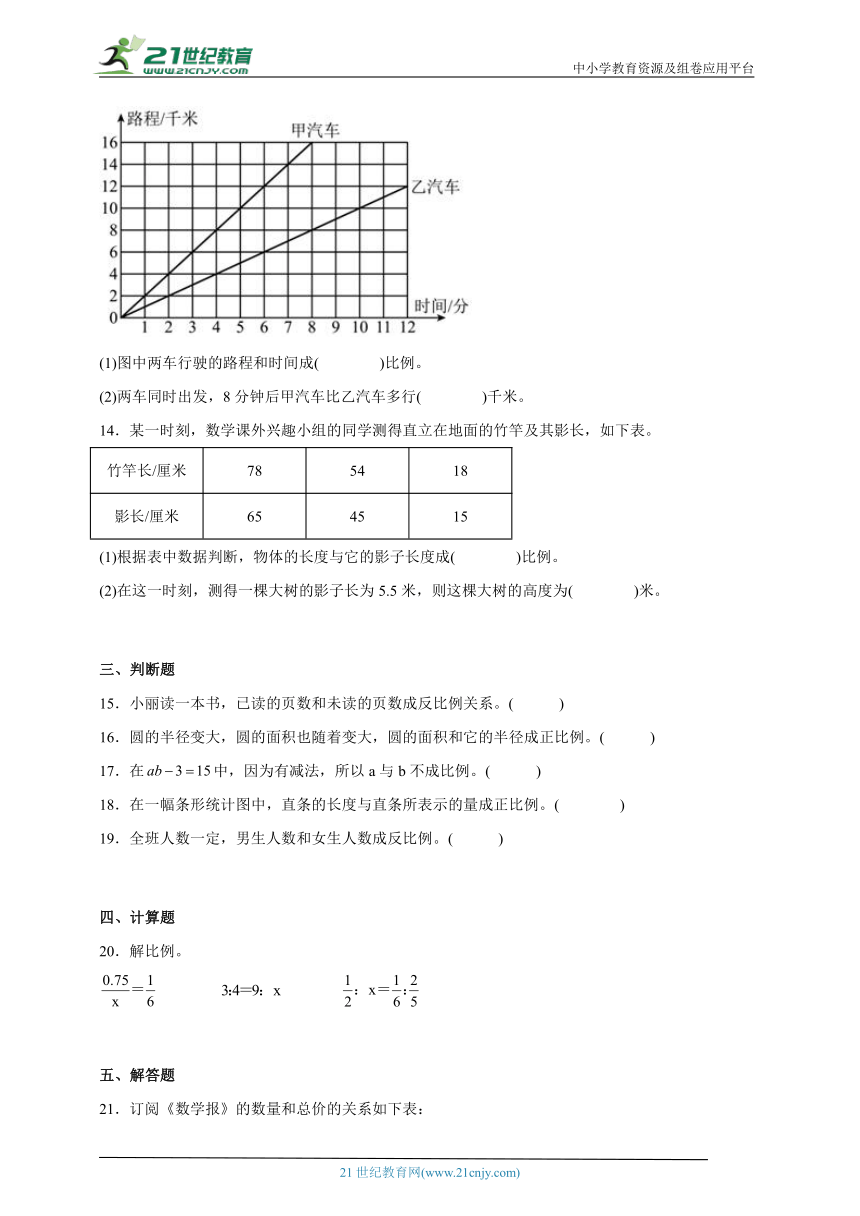
13.下边的图像表示甲、乙两辆汽车行驶的时间和路程情况。
(1)图中两车行驶的路程和时间成( )比例。
(2)两车同时出发,8分钟后甲汽车比乙汽车多行( )千米。
14.某一时刻,数学课外兴趣小组的同学测得直立在地面的竹竿及其影长,如下表。
竹竿长/厘米 78 54 18
影长/厘米 65 45 15
(1)根据表中数据判断,物体的长度与它的影子长度成( )比例。
(2)在这一时刻,测得一棵大树的影子长为5.5米,则这棵大树的高度为( )米。
三、判断题
15.小丽读一本书,已读的页数和未读的页数成反比例关系。( )
16.圆的半径变大,圆的面积也随着变大,圆的面积和它的半径成正比例。( )
17.在中,因为有减法,所以a与b不成比例。( )
18.在一幅条形统计图中,直条的长度与直条所表示的量成正比例。( )
19.全班人数一定,男生人数和女生人数成反比例。( )
四、计算题
20.解比例。
五、解答题
21.订阅《数学报》的数量和总价的关系如下表:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 240 280 …
(1)将表格补充完整,根据表中的数据,在下图中描出《数学报》总价和数量所对应的点,再按顺序连接起来。
(2)题目中( )没变,总价和数量成( )比例。
(3)从图中可以推算出,如果订阅9份《数学报》,需要( )元。
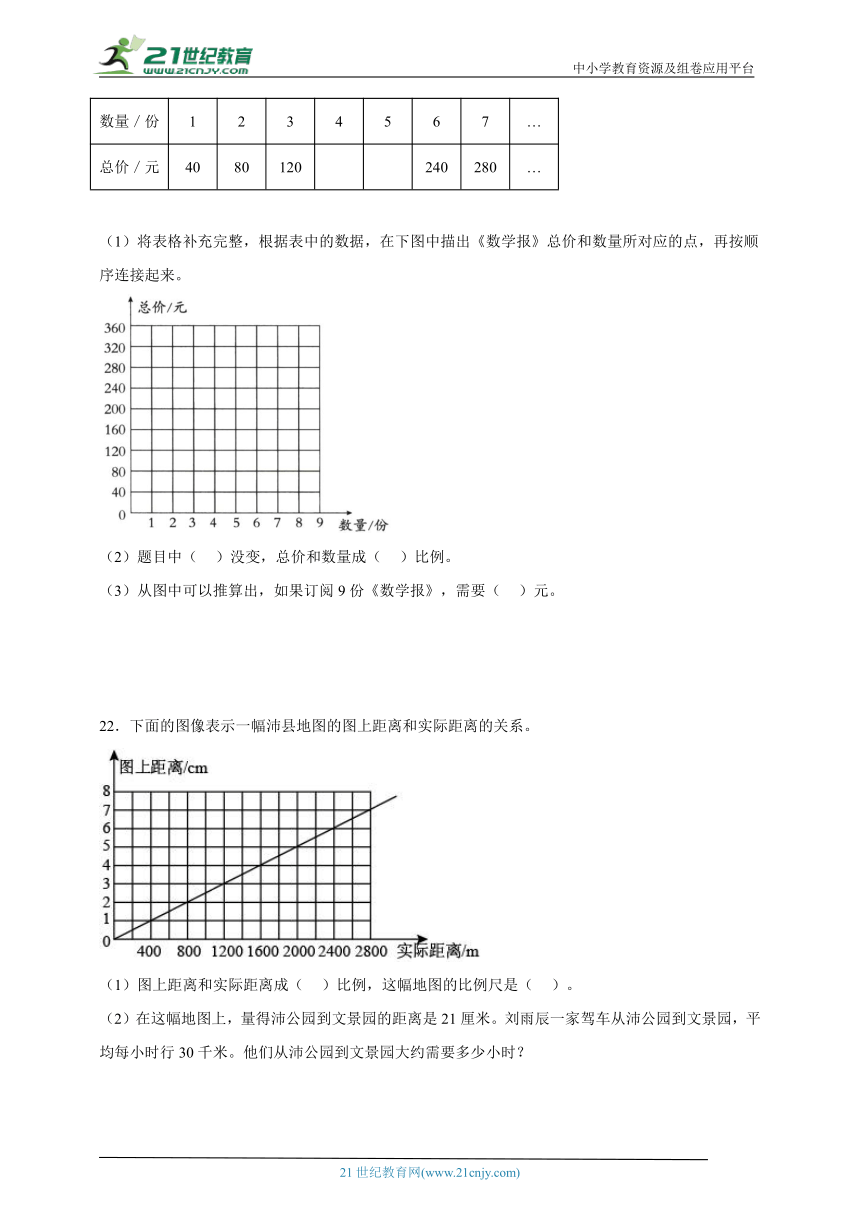
22.下面的图像表示一幅沛县地图的图上距离和实际距离的关系。
(1)图上距离和实际距离成( )比例,这幅地图的比例尺是( )。
(2)在这幅地图上,量得沛公园到文景园的距离是21厘米。刘雨辰一家驾车从沛公园到文景园,平均每小时行30千米。他们从沛公园到文景园大约需要多少小时?
23.如图,甲、乙两车运货的吨数与次数的关系如图。
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
24.每本演算本售价1.5元,购买2本、3本……分别需要多少元?
数量/本 0 1 2 3 4 5 6 …
总价/元 0 1.5 3 4.5 6 7.5 9 …
(1)购买演算本的总价与数量成( )比例。
(2)把上表中演算本的数量与总价所对应的点描在方格纸上,再顺次连接。
(3)购买90本演算本需要( )元。
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的( )倍。
25.如图是水龙头打开后水量情况统计图。
①看图填表:
时间(秒) 30 ( )
出水量(升) ( ) 22
②水龙头打开的时间和出水量成( )比例。
参考答案:
1.B
【分析】比的基本性质:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变;
含盐率=盐的质量÷盐水的质量×100%;
两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系;
图上距离∶实际距离=比例尺,据此解答。
【详解】A.比的前项乘0.5,后项除以2,等于乘,即乘0.5,根据比的基本性质,比值不变,说法正确;
B.盐的质量为100×10%+5=15(克),则含盐率为15÷(100+5)×100%≈14.3%,本选项说法错误;
C.因为圆柱的底面周长×高=2×π×底面半径×高=圆柱的侧面积(一定),是对应的乘积一定,所以它的高和底面半径成反比例,本选项正确;
D.比例尺=图上距离∶实际距离,所以一幅图的比例尺为100∶1,表示图上距离是实际距离的100倍,本选项说法正确。
故答案为:B
【点睛】本题考查了比的基本性质、百分率的应用、反比例的辨认、比例尺的意义等。熟练掌握相关知识是解题的关键。
2.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此逐项分析,进行解答。
【详解】A.长方形面积=长×宽;长方形面积一定,乘积一定,长和宽成反比例;
B.一个人的年龄和头发长度既不是比值一定,也不是乘积一定,所以一个人的年龄和头发长度不成比例;
C.路程÷速度=时间(一定),比值一定,路程和速度成正比例;
D.全班人数-女生人数=男生人数(一定),和一定,所以女生人数和全班人数不成比例。
故答案为:C
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
3.A
【分析】根据比例尺的意义,图上距离和实际距离的比叫做比例尺,据此求出这幅地图的比例尺,即1∶30=2∶60=,因为图上距离∶实际距离=比例尺(一定),所以图上距离和实际距离成正比例。
【详解】由分析可知:图上距离和实际距离成正比例。
故答案为:A
【点睛】本题主要考查正比例的判断方法,要注意正比例的图像要经过原点并且是一条直线。
4.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,由此对给出的选项逐一分析,做出判断。
【详解】A.因为总钱数÷人数=《小学生数学报》的单价(一定),所以订阅《小学生数学报》的人数与总钱数成正比例,说法正确。
B.因为同时同地,物体高度与影长的比值一定,所以同一时间,物体的高度和影长成正比例,说法正确。
C.因为(长+宽)×2=长方形周长,长和宽是和的形式,所以不成比例。所以说法错误。
D.因为每块砖的面积×铺砖的块数=铺地面积(一定),所以每块砖的面积和铺砖的块数成反比例。说法正确。
故答案为:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
根据比例的基本性质:两个的内项之积等于两个外项之积;据此解答。
【详解】A.4x=3y,x∶y=3∶4=,比值一定,x与y成正比例;原题说法错误;
B.4x=3÷y,x∶y=3÷4=,比值一定,x与y成正比例;原题说法错误;
C.在一个比例中,若交换一个比的前项和后项的位置,则外项之积不等于内项之积,则比例关系不成立,所以原题说法错误;
D.在一个比例中,若交换两个外项或两个内向的位置,内项之积仍等于外项之积,则比例关系仍成立。
故答案为:D
【点睛】利用正比例意义和辨别、反比例意义和辨别、以及比例的基本性质进行解答。
6.A
【分析】正反比例判断方法是:两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值一定,它们的关系叫做正比例关系;如果两个量的积一定,它们的关系叫做反比例关系。
【详解】书的总字数书的页数每页书的字数(一定),即比值一定,所以书的页数和书的总字数成正比例关系。
故答案为:A
【点睛】根据根据正比例意义和辨别,反比例意义和辨别进行解答。
7. 直径##半径 反
【分析】两种相关联的量,如果它们的比值一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】圆的周长C=πd=2πr,则=π、=2π,圆的周长与直径的比值、圆的周长与半径的比值都一定,那么圆的周长与它的直径或半径成正比例;6÷x=y,则xy=6,x和y的乘积一定,那么x与y成反比例。
【点睛】本题考查正比例和反比例的辨认。掌握正比例和反比例的意义是解题的关键。
8. B 正
【分析】根据A、B是两个非零自然数,A=B,即B=8A,知道A和B为倍数关系,B是A的8倍,再根据成倍数关系的两个数中较大数是这两个数的最小公倍数求解;根据判断两个相关联的量成什么比例的方法,看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】因为A=B,B=8A,所以A和B的最小公倍数是B;
因为A÷B=(一定),比值一定,成正比例。
【点睛】本题考查了当两个数成倍数关系时,求这两个数的最小公倍数的方法及判断两个相关联的量成什么比例的方法。
9. 4 8.5 10.9 坐车的路程 应付的钱数 不成
【分析】首先根据总价=单价×数量,用4+(5-2)×1.5,求出5公里需要多少钱;然后用6减去5,再乘以1.5×(1+60%),求出超过的部分需要的钱数,再加上5公里需要的钱数,求出6公里的路需要多少钱即可;最后判断出坐车的路程和应付的钱数是两种相关联的量,它们之间不成比例关系即可。
【详解】2公里需要的钱数:4元
5公里需要的钱数:4+(5-2)×1.5
=4+3×1.5
=4+4.5
=8.5(元)
6公里需要的钱数:
4+(5-2)×1.5+(6-5)×1.5×(1+60%)
=4+4.5+1.5×1.6
=8.5+2.4
=10.9(元)
坐车的路程公里 应付的钱数元
2 4
5 8.5
6 10.9
从上表可以发现坐车的路程和应付的钱数两种相关联的量;因为, ,可知应付的钱数和坐车的路程的比值不是定值,所以它们之间不成比例关系。
【点睛】此题主要考查了正、反比例的意义的应用,这也是一道关于分段计费在实际中的应用的题目,关键在于根据题目已知条件找准相应的分段计费方法。
10. 4 12 100 50
【分析】x与y成反比例关系,也就是x与y的乘积是一定(相等)的。根据对应的x与y都是已知的一栏,可求出乘积,然后根据已知项,求出未知项填入。
【详解】
填表如下:
2 0.1 4 12
5 100 2.5 50
【点睛】掌握反比例的意义及反比例的应用解答本题的关键。
11.5
【分析】如果A与B成正比例,则A与B的比值一定,根据比值一定,列出比例式,再依据比例的基本性质求得A的数值。
【详解】解:设?为A。
10∶8=A∶4
8A=40
A=5
【点睛】此题考查根据相关联的两个量成正比例关系,列方程或比例求一个未知量的问题。
12.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答。
【详解】A×B=C,C一定,也就是积一定,A和B成反比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
13.(1)正
(2)8
【分析】(1)观察图形可知,是经过原点的直线;从图像中很清晰地看出甲、乙两辆汽车行驶的路程和行驶时间同时扩大(或缩小)的变化规律,只要是两种相关联的量变化方向相同,就是说明它们的比值一定,这两种量就成正比例关系,据此解答;
(2)找出时间轴上的8分钟,它在两条图上应对的路程,两路程的差就是要求的答案。
(1)
图中两车行驶的路程和时间成正比例。
(2)
8分钟甲车行驶16千米,乙车行驶8千米。
16-8=8(千米)
【点睛】借助直观的图像,辨别两种相关联的量成什么比例,只要图像是一条直线,就成正比例;图像是一条曲线,就成反比例,再根据成什么比例解答问题。
14.(1)正
(2)6.6
【分析】(1)根据统计表计算竹竿长和影长的比,18∶15=,54∶45=,75∶56=,竹竿长和影长的比值相等,竹竿长和影长成正比例关系;据此判断即可。
(2)物体的长度与它的影子长度成正比例,比值是,所以树高∶树影长=,可得树高=树影长×。
(1)
18∶15=,54∶45=,75∶56=,
竹竿长和影长的比值相等,竹竿长和影长成正比例关系;
所以,物体的长度与它的影子长度成正比例;
(2)
5.5×=6.6(米)
【点睛】根据两个量比值相等,找出题中的数量成正比例关系,根据成正比例的两个量比值相等解决问题。
15.×
【分析】根据xy=k(一定),x和y成反比例关系,进行分析。
【详解】已读的页数+未读的页数=总页数,和一定,已读的页数和未读的页数不成比例关系,所以原题说法错误。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
16.×
【分析】判断两个相关联的量之间是否成正比例,就看这两个量对应的比值,如果是比值一定,就成正比例,据此解答。
【详解】圆的面积÷半径的平方=圆周率(一定),比值一定,圆的面积和它半径的平方成正比例,但圆的面积与半径的比值不是一定的,不符合正比例的意义,所以圆的面积和半径不成正比例。
故答案为:×
【点睛】此题属于辨识成正比例的量,就看这两个量对应的比值,再做判断。
17.×
【分析】相关联的两个量,如果它们的乘积一定,则这两个量成反比例关系。
【详解】ab 3=15,所以有:ab=18,因此a与b成反比例,因此题干表述错误。
故答案为:×。
【点睛】本题考查反比例,解答本题的关键是掌握反比例的含义。
18.√
【分析】如果两种量对应的比值一定,成正比例关系;如果两种量对应的乘积一定,则成反比例关系,据此判断。
【详解】条形统计图中,直条的单位长度表示的量是一定的,直条的单位长度表示的量=直条表示的量÷直条的长度,所以直条的长度与直条所表示的量成正比例。说法正确。
故答案为:√
【点睛】此题考查了正反比例的辨别,主要是看两个变化的量是乘积一定还是比值一定。
19.×
【分析】根据反比例的意义:两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的乘积一定,即xy=k(定值),那么这两个量叫做成反比例的量,它们的关系叫做反比例关系;解答即可。
【详解】男生人数+女生人数=全班人数(和一定),不符合反比例意义,原题说法错误。
故答案为:×
【点睛】本题主要考查反比例的意义,解题时要明确:只有乘积一定的两种相关联的两种量,才成反比例。
20.x=4.5;x=12;x=
【分析】(1)根据比例的基本性质得x=0.75×6,继而解出比例;
(2)根据比例的基本性质得3x=4×9,再根据等式的性质,把这个方程两边同时除以3即可解答;
(3)根据比例的基本性质得x=,再把方程两边同时乘6即可解答。
【详解】
解:x=0.75×6
x=4.5
解:3x=4×9
3x=36
x=12
解:x=
x=×6
x=
21.(1)见详解;
(2)单价;正;
(3)360
【分析】(1)由统计表可知:《数学报》的单价是40元,根据单价×数量=总价,分别求出4份、5份的总价,填表即可,根据统计表中数据描点连线即可;
(2)由统计表可知:总价÷数量=单价(40元)不变,据此解答。
(3)根据总价=单价×数量直接计算即可。
【详解】(1)4×40=160(元)
5×40=200(元)
填表画图如下:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 160 200 240 280 …
(2)题目中单价没变,总价和数量成正比例。
(3)40×9=360(元)
【点睛】本题主要考查正比例的意义与辨识及统计图表的综合应用。
22.(1)正;1∶40000;
(2)0.28小时
【分析】(1)根据图可知,这个直线是经过原点的直线,由此即可知道图上距离与实际距离成正比例关系;根据比例尺=图上距离∶实际距离,把数代入即可。注意统一单位。
(2)根据实际距离=图上距离÷比例尺,把数代入求出沛公园到文景园的路程,再根据公式:路程÷速度=时间,把数代入即可求解。
【详解】(1)根据图可知:图上距离和实际距离成正比例;
2800m=280000cm
比例尺=7厘米∶280000厘米=1∶40000
(2)21÷=840000(厘米)
840000厘米=8.4千米
8.4÷30=0.28(小时)
答:他们从沛公园到文景园大约需要0.28小时。
【点睛】解答此题的关键是根据图中数据分析出图上距离和实际距离的关系;并且熟练掌握比例尺和行程问题的公式并灵活运用。
23.(1)正比例;正比例
(2)12吨
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
(1)根据图中数据,算一算甲、乙中两种变量之间的比值是否一定即可。
(2)先求出1次甲比乙多运多少,再求出6次甲比乙多运多少即可。
【详解】(1)甲:====6(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系;
乙:====4(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系。
答:甲车的运货量与运货次数成正比例关系,乙车的运货量与运货次数成正比例关系。
(2)18÷3-12÷3
=6-4
=2(吨)
2×6=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨。
【点睛】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值。
24.(1)正
(2)见详解
(3)135
(4)4
【分析】(1)因为=单价(一定),所以总价和数量成正比例。
(2)根据表格数据作图即可求解。
(3)根据单价×数量=总价,计算出购买90本演算本需要多少元。
(4)因为单价一定,总价和数量成正比例,所以奇思购买的演算本的数量是妙想的4倍,他花的钱是妙想的4倍。据此解答。
【详解】(1)购买演算本的总价与数量成正比例。
(2)如图所示:
(3)1.5×90=135(元)
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的4倍。
【点睛】此题考查的目的是理解掌握正比例的意义及应用,以及统计表的特点、作用,明确:正比例图象是一条直线。
25. 55 12 正
【分析】观察折线统计图可知:这个水龙头打开30秒出水量是12升,出水量与时间的比值是:30∶12=、当水龙头开40秒时,出水量是16升、出水量与时间的比值是:40∶16=,可以判断出水量与打开水龙头的时间成正比。从而求得当出水量为22升时所用的时间。 据此解答。
【详解】①
因为30∶12=40∶16=
所以水龙头打开时间与出水量成正比。
当出水量是22升时,所用时间是:
22×=55(秒)
(2)因为30∶12=40∶16=(一定),
是这个水龙头的出水量和打开的时间的比值一定,
符合正比例的意义,所以这个水龙头打开的时间和出水量成成正比例。
【点睛】此题考查根据统计图中得到的数据完成统计表,也考查了判断成正、反比例的方法:看两个相关联的量的乘积一定还是比值一定,如果乘积一定,则两种量成反比例;如果比值一定,则两种量则成正比例。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.下面四句话中不正确的一句是( )。
A.比的前项乘0.5,比的后项除以2,比值不变
B.100克含盐率为10%的盐水中加入5克盐,含盐达到15%
C.圆柱体的侧面积一定,则它的高和底面半径成反比例
D.一幅图的比例尺为100∶1,表示图上距离是实际距离的100倍
2.下面每组的两个量中,成正比例关系的是( )。
A.长方形的面积一定,长和宽 B.一个人的年龄和头发长度
C.时间一定,路程和速度 D.男生人数一定,女生人数和全班人数
3.根据下面的图像可以知道,图上距离和实际距离( )。
A.成正比例 B.成反比例 C.不成比例 D.无法判断
4.下面说法不正确的是( )。
A.订阅《小学生数学报》的人数与总钱数成正比例。
B.同一时间,物体的高度和影长成正比例。
C.长方形的周长一定,长和宽成反比例。
D.给一个房间地面铺砖,每块砖的面积和铺砖的块数成反比例。
5.下列说法正确的是( )。
A.若,则与成反比例
B.若,则和成正比例
C.在一个比例中,若交换一个比的前项和后项的位置,则比例关系仍成立
D.在一个比例中,若交换两个外项或两个内项的位置,则比例关系仍成立
6.每页书的字数一定,书的页数和书的总字数( )。
A.成正比例关系 B.成反比例关系 C.不成比例关系 D.无法判断
二、填空题
7.圆的周长与它的( )成正比例;如果6÷x=y,那么x与y成( )比例。
8.A、B是两个非零自然数,如果A=B,那么A和B的最小公倍数是( ),A和B成( )比例。
9.某市出租公司有这样的规定,起步价4元(2公里之内),超过2公里而在5公里之内(含5公里),每公里按1.5元计价,5公里以上部分每公里再加价。
坐车的路程公里 应付的钱数元
2 ( )
5 ( )
6 ( )
从上表中你发现有( )和( )两种相关联的量,它们之间是( )比例关系。
10.下表中与两个量成反比例关系,请把表格填完整。
2 0.1 ( ) ( )
5 ( ) 2.5 ( )
11.图中,若与成正比例,则“?”是( )。
10 ?
8 4
12.、B、C三量的关系式A×B=C中,当C一定时,A和B成( )关系。
13.下边的图像表示甲、乙两辆汽车行驶的时间和路程情况。
(1)图中两车行驶的路程和时间成( )比例。
(2)两车同时出发,8分钟后甲汽车比乙汽车多行( )千米。
14.某一时刻,数学课外兴趣小组的同学测得直立在地面的竹竿及其影长,如下表。
竹竿长/厘米 78 54 18
影长/厘米 65 45 15
(1)根据表中数据判断,物体的长度与它的影子长度成( )比例。
(2)在这一时刻,测得一棵大树的影子长为5.5米,则这棵大树的高度为( )米。
三、判断题
15.小丽读一本书,已读的页数和未读的页数成反比例关系。( )
16.圆的半径变大,圆的面积也随着变大,圆的面积和它的半径成正比例。( )
17.在中,因为有减法,所以a与b不成比例。( )
18.在一幅条形统计图中,直条的长度与直条所表示的量成正比例。( )
19.全班人数一定,男生人数和女生人数成反比例。( )
四、计算题
20.解比例。
五、解答题
21.订阅《数学报》的数量和总价的关系如下表:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 240 280 …
(1)将表格补充完整,根据表中的数据,在下图中描出《数学报》总价和数量所对应的点,再按顺序连接起来。
(2)题目中( )没变,总价和数量成( )比例。
(3)从图中可以推算出,如果订阅9份《数学报》,需要( )元。
22.下面的图像表示一幅沛县地图的图上距离和实际距离的关系。
(1)图上距离和实际距离成( )比例,这幅地图的比例尺是( )。
(2)在这幅地图上,量得沛公园到文景园的距离是21厘米。刘雨辰一家驾车从沛公园到文景园,平均每小时行30千米。他们从沛公园到文景园大约需要多少小时?
23.如图,甲、乙两车运货的吨数与次数的关系如图。
(1)甲车的运货量与运货次数成什么比例关系?乙车呢?
(2)甲、乙两车各运货6次,运货量相差多少吨?
24.每本演算本售价1.5元,购买2本、3本……分别需要多少元?
数量/本 0 1 2 3 4 5 6 …
总价/元 0 1.5 3 4.5 6 7.5 9 …
(1)购买演算本的总价与数量成( )比例。
(2)把上表中演算本的数量与总价所对应的点描在方格纸上,再顺次连接。
(3)购买90本演算本需要( )元。
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的( )倍。
25.如图是水龙头打开后水量情况统计图。
①看图填表:
时间(秒) 30 ( )
出水量(升) ( ) 22
②水龙头打开的时间和出水量成( )比例。
参考答案:
1.B
【分析】比的基本性质:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变;
含盐率=盐的质量÷盐水的质量×100%;
两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系;
图上距离∶实际距离=比例尺,据此解答。
【详解】A.比的前项乘0.5,后项除以2,等于乘,即乘0.5,根据比的基本性质,比值不变,说法正确;
B.盐的质量为100×10%+5=15(克),则含盐率为15÷(100+5)×100%≈14.3%,本选项说法错误;
C.因为圆柱的底面周长×高=2×π×底面半径×高=圆柱的侧面积(一定),是对应的乘积一定,所以它的高和底面半径成反比例,本选项正确;
D.比例尺=图上距离∶实际距离,所以一幅图的比例尺为100∶1,表示图上距离是实际距离的100倍,本选项说法正确。
故答案为:B
【点睛】本题考查了比的基本性质、百分率的应用、反比例的辨认、比例尺的意义等。熟练掌握相关知识是解题的关键。
2.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此逐项分析,进行解答。
【详解】A.长方形面积=长×宽;长方形面积一定,乘积一定,长和宽成反比例;
B.一个人的年龄和头发长度既不是比值一定,也不是乘积一定,所以一个人的年龄和头发长度不成比例;
C.路程÷速度=时间(一定),比值一定,路程和速度成正比例;
D.全班人数-女生人数=男生人数(一定),和一定,所以女生人数和全班人数不成比例。
故答案为:C
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
3.A
【分析】根据比例尺的意义,图上距离和实际距离的比叫做比例尺,据此求出这幅地图的比例尺,即1∶30=2∶60=,因为图上距离∶实际距离=比例尺(一定),所以图上距离和实际距离成正比例。
【详解】由分析可知:图上距离和实际距离成正比例。
故答案为:A
【点睛】本题主要考查正比例的判断方法,要注意正比例的图像要经过原点并且是一条直线。
4.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,由此对给出的选项逐一分析,做出判断。
【详解】A.因为总钱数÷人数=《小学生数学报》的单价(一定),所以订阅《小学生数学报》的人数与总钱数成正比例,说法正确。
B.因为同时同地,物体高度与影长的比值一定,所以同一时间,物体的高度和影长成正比例,说法正确。
C.因为(长+宽)×2=长方形周长,长和宽是和的形式,所以不成比例。所以说法错误。
D.因为每块砖的面积×铺砖的块数=铺地面积(一定),所以每块砖的面积和铺砖的块数成反比例。说法正确。
故答案为:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
5.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
根据比例的基本性质:两个的内项之积等于两个外项之积;据此解答。
【详解】A.4x=3y,x∶y=3∶4=,比值一定,x与y成正比例;原题说法错误;
B.4x=3÷y,x∶y=3÷4=,比值一定,x与y成正比例;原题说法错误;
C.在一个比例中,若交换一个比的前项和后项的位置,则外项之积不等于内项之积,则比例关系不成立,所以原题说法错误;
D.在一个比例中,若交换两个外项或两个内向的位置,内项之积仍等于外项之积,则比例关系仍成立。
故答案为:D
【点睛】利用正比例意义和辨别、反比例意义和辨别、以及比例的基本性质进行解答。
6.A
【分析】正反比例判断方法是:两种相关联的量,一种量变化,另一种量也随着变化。如果这两种量中相对应的两个数比值一定,它们的关系叫做正比例关系;如果两个量的积一定,它们的关系叫做反比例关系。
【详解】书的总字数书的页数每页书的字数(一定),即比值一定,所以书的页数和书的总字数成正比例关系。
故答案为:A
【点睛】根据根据正比例意义和辨别,反比例意义和辨别进行解答。
7. 直径##半径 反
【分析】两种相关联的量,如果它们的比值一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】圆的周长C=πd=2πr,则=π、=2π,圆的周长与直径的比值、圆的周长与半径的比值都一定,那么圆的周长与它的直径或半径成正比例;6÷x=y,则xy=6,x和y的乘积一定,那么x与y成反比例。
【点睛】本题考查正比例和反比例的辨认。掌握正比例和反比例的意义是解题的关键。
8. B 正
【分析】根据A、B是两个非零自然数,A=B,即B=8A,知道A和B为倍数关系,B是A的8倍,再根据成倍数关系的两个数中较大数是这两个数的最小公倍数求解;根据判断两个相关联的量成什么比例的方法,看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】因为A=B,B=8A,所以A和B的最小公倍数是B;
因为A÷B=(一定),比值一定,成正比例。
【点睛】本题考查了当两个数成倍数关系时,求这两个数的最小公倍数的方法及判断两个相关联的量成什么比例的方法。
9. 4 8.5 10.9 坐车的路程 应付的钱数 不成
【分析】首先根据总价=单价×数量,用4+(5-2)×1.5,求出5公里需要多少钱;然后用6减去5,再乘以1.5×(1+60%),求出超过的部分需要的钱数,再加上5公里需要的钱数,求出6公里的路需要多少钱即可;最后判断出坐车的路程和应付的钱数是两种相关联的量,它们之间不成比例关系即可。
【详解】2公里需要的钱数:4元
5公里需要的钱数:4+(5-2)×1.5
=4+3×1.5
=4+4.5
=8.5(元)
6公里需要的钱数:
4+(5-2)×1.5+(6-5)×1.5×(1+60%)
=4+4.5+1.5×1.6
=8.5+2.4
=10.9(元)
坐车的路程公里 应付的钱数元
2 4
5 8.5
6 10.9
从上表可以发现坐车的路程和应付的钱数两种相关联的量;因为, ,可知应付的钱数和坐车的路程的比值不是定值,所以它们之间不成比例关系。
【点睛】此题主要考查了正、反比例的意义的应用,这也是一道关于分段计费在实际中的应用的题目,关键在于根据题目已知条件找准相应的分段计费方法。
10. 4 12 100 50
【分析】x与y成反比例关系,也就是x与y的乘积是一定(相等)的。根据对应的x与y都是已知的一栏,可求出乘积,然后根据已知项,求出未知项填入。
【详解】
填表如下:
2 0.1 4 12
5 100 2.5 50
【点睛】掌握反比例的意义及反比例的应用解答本题的关键。
11.5
【分析】如果A与B成正比例,则A与B的比值一定,根据比值一定,列出比例式,再依据比例的基本性质求得A的数值。
【详解】解:设?为A。
10∶8=A∶4
8A=40
A=5
【点睛】此题考查根据相关联的两个量成正比例关系,列方程或比例求一个未知量的问题。
12.反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此解答。
【详解】A×B=C,C一定,也就是积一定,A和B成反比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
13.(1)正
(2)8
【分析】(1)观察图形可知,是经过原点的直线;从图像中很清晰地看出甲、乙两辆汽车行驶的路程和行驶时间同时扩大(或缩小)的变化规律,只要是两种相关联的量变化方向相同,就是说明它们的比值一定,这两种量就成正比例关系,据此解答;
(2)找出时间轴上的8分钟,它在两条图上应对的路程,两路程的差就是要求的答案。
(1)
图中两车行驶的路程和时间成正比例。
(2)
8分钟甲车行驶16千米,乙车行驶8千米。
16-8=8(千米)
【点睛】借助直观的图像,辨别两种相关联的量成什么比例,只要图像是一条直线,就成正比例;图像是一条曲线,就成反比例,再根据成什么比例解答问题。
14.(1)正
(2)6.6
【分析】(1)根据统计表计算竹竿长和影长的比,18∶15=,54∶45=,75∶56=,竹竿长和影长的比值相等,竹竿长和影长成正比例关系;据此判断即可。
(2)物体的长度与它的影子长度成正比例,比值是,所以树高∶树影长=,可得树高=树影长×。
(1)
18∶15=,54∶45=,75∶56=,
竹竿长和影长的比值相等,竹竿长和影长成正比例关系;
所以,物体的长度与它的影子长度成正比例;
(2)
5.5×=6.6(米)
【点睛】根据两个量比值相等,找出题中的数量成正比例关系,根据成正比例的两个量比值相等解决问题。
15.×
【分析】根据xy=k(一定),x和y成反比例关系,进行分析。
【详解】已读的页数+未读的页数=总页数,和一定,已读的页数和未读的页数不成比例关系,所以原题说法错误。
【点睛】关键是理解反比例的意义,积一定是反比例关系。
16.×
【分析】判断两个相关联的量之间是否成正比例,就看这两个量对应的比值,如果是比值一定,就成正比例,据此解答。
【详解】圆的面积÷半径的平方=圆周率(一定),比值一定,圆的面积和它半径的平方成正比例,但圆的面积与半径的比值不是一定的,不符合正比例的意义,所以圆的面积和半径不成正比例。
故答案为:×
【点睛】此题属于辨识成正比例的量,就看这两个量对应的比值,再做判断。
17.×
【分析】相关联的两个量,如果它们的乘积一定,则这两个量成反比例关系。
【详解】ab 3=15,所以有:ab=18,因此a与b成反比例,因此题干表述错误。
故答案为:×。
【点睛】本题考查反比例,解答本题的关键是掌握反比例的含义。
18.√
【分析】如果两种量对应的比值一定,成正比例关系;如果两种量对应的乘积一定,则成反比例关系,据此判断。
【详解】条形统计图中,直条的单位长度表示的量是一定的,直条的单位长度表示的量=直条表示的量÷直条的长度,所以直条的长度与直条所表示的量成正比例。说法正确。
故答案为:√
【点睛】此题考查了正反比例的辨别,主要是看两个变化的量是乘积一定还是比值一定。
19.×
【分析】根据反比例的意义:两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的乘积一定,即xy=k(定值),那么这两个量叫做成反比例的量,它们的关系叫做反比例关系;解答即可。
【详解】男生人数+女生人数=全班人数(和一定),不符合反比例意义,原题说法错误。
故答案为:×
【点睛】本题主要考查反比例的意义,解题时要明确:只有乘积一定的两种相关联的两种量,才成反比例。
20.x=4.5;x=12;x=
【分析】(1)根据比例的基本性质得x=0.75×6,继而解出比例;
(2)根据比例的基本性质得3x=4×9,再根据等式的性质,把这个方程两边同时除以3即可解答;
(3)根据比例的基本性质得x=,再把方程两边同时乘6即可解答。
【详解】
解:x=0.75×6
x=4.5
解:3x=4×9
3x=36
x=12
解:x=
x=×6
x=
21.(1)见详解;
(2)单价;正;
(3)360
【分析】(1)由统计表可知:《数学报》的单价是40元,根据单价×数量=总价,分别求出4份、5份的总价,填表即可,根据统计表中数据描点连线即可;
(2)由统计表可知:总价÷数量=单价(40元)不变,据此解答。
(3)根据总价=单价×数量直接计算即可。
【详解】(1)4×40=160(元)
5×40=200(元)
填表画图如下:
数量/份 1 2 3 4 5 6 7 …
总价/元 40 80 120 160 200 240 280 …
(2)题目中单价没变,总价和数量成正比例。
(3)40×9=360(元)
【点睛】本题主要考查正比例的意义与辨识及统计图表的综合应用。
22.(1)正;1∶40000;
(2)0.28小时
【分析】(1)根据图可知,这个直线是经过原点的直线,由此即可知道图上距离与实际距离成正比例关系;根据比例尺=图上距离∶实际距离,把数代入即可。注意统一单位。
(2)根据实际距离=图上距离÷比例尺,把数代入求出沛公园到文景园的路程,再根据公式:路程÷速度=时间,把数代入即可求解。
【详解】(1)根据图可知:图上距离和实际距离成正比例;
2800m=280000cm
比例尺=7厘米∶280000厘米=1∶40000
(2)21÷=840000(厘米)
840000厘米=8.4千米
8.4÷30=0.28(小时)
答:他们从沛公园到文景园大约需要0.28小时。
【点睛】解答此题的关键是根据图中数据分析出图上距离和实际距离的关系;并且熟练掌握比例尺和行程问题的公式并灵活运用。
23.(1)正比例;正比例
(2)12吨
【分析】成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
(1)根据图中数据,算一算甲、乙中两种变量之间的比值是否一定即可。
(2)先求出1次甲比乙多运多少,再求出6次甲比乙多运多少即可。
【详解】(1)甲:====6(一定),是比值一定,所以甲车的运货量与运货次数成正比例关系;
乙:====4(一定),是比值一定,所以乙车的运货量与运货次数成正比例关系。
答:甲车的运货量与运货次数成正比例关系,乙车的运货量与运货次数成正比例关系。
(2)18÷3-12÷3
=6-4
=2(吨)
2×6=12(吨)
答:甲、乙两车各运货6次,运货量相差12吨。
【点睛】此题考查成正比例量,判定两个变化的量是不是成正比例关系,关键是看两个量的比值是否为定值。
24.(1)正
(2)见详解
(3)135
(4)4
【分析】(1)因为=单价(一定),所以总价和数量成正比例。
(2)根据表格数据作图即可求解。
(3)根据单价×数量=总价,计算出购买90本演算本需要多少元。
(4)因为单价一定,总价和数量成正比例,所以奇思购买的演算本的数量是妙想的4倍,他花的钱是妙想的4倍。据此解答。
【详解】(1)购买演算本的总价与数量成正比例。
(2)如图所示:
(3)1.5×90=135(元)
(4)奇思购买的演算本的数量是妙想的4倍,他花的钱数是妙想的4倍。
【点睛】此题考查的目的是理解掌握正比例的意义及应用,以及统计表的特点、作用,明确:正比例图象是一条直线。
25. 55 12 正
【分析】观察折线统计图可知:这个水龙头打开30秒出水量是12升,出水量与时间的比值是:30∶12=、当水龙头开40秒时,出水量是16升、出水量与时间的比值是:40∶16=,可以判断出水量与打开水龙头的时间成正比。从而求得当出水量为22升时所用的时间。 据此解答。
【详解】①
因为30∶12=40∶16=
所以水龙头打开时间与出水量成正比。
当出水量是22升时,所用时间是:
22×=55(秒)
(2)因为30∶12=40∶16=(一定),
是这个水龙头的出水量和打开的时间的比值一定,
符合正比例的意义,所以这个水龙头打开的时间和出水量成成正比例。
【点睛】此题考查根据统计图中得到的数据完成统计表,也考查了判断成正、反比例的方法:看两个相关联的量的乘积一定还是比值一定,如果乘积一定,则两种量成反比例;如果比值一定,则两种量则成正比例。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
