8.2.1一元线性回归模型及其参数的最小二乘估计 课件(共53张PPT)
文档属性
| 名称 | 8.2.1一元线性回归模型及其参数的最小二乘估计 课件(共53张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 08:03:39 | ||
图片预览










文档简介
(共53张PPT)
8.2.1一元线性回归模型及其参数的最小二乘估计
人教A版2019必修第三册
1. 样本相关系数:
2.相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数据的线性相关程度越弱;特别地,当|r|=0时,成对数据的没有线性相关关系;当|r|=1时,成对数据都落在一条直线上.
通过前面的学习我们已经了解到,根据成对样本数据的散点图和样本相关系数,可以推断两个变量是否存在相关关系、是正相关还是负相关,以及线性相关程度的强弱等. 进一步地,如果能像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型刻画两个随机变量的相关关系,那么我们就可以利用这个模型研究两个变量之间的随机关系,并通过模型进行预测.
下面我们研究当两个变量线性相关时,如何利用成对样本数据建立统计模型,并利用模型进行预测的问题.
问题1:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
可以发现,散点大致分布在一条从左下角到右上角的直线附近,表明儿子身高和父亲身高线性相关.利用统计软件,求得样本相关系数为r≈0.886,表明儿子身高和父亲身高正线性相关,且相关程度较高。
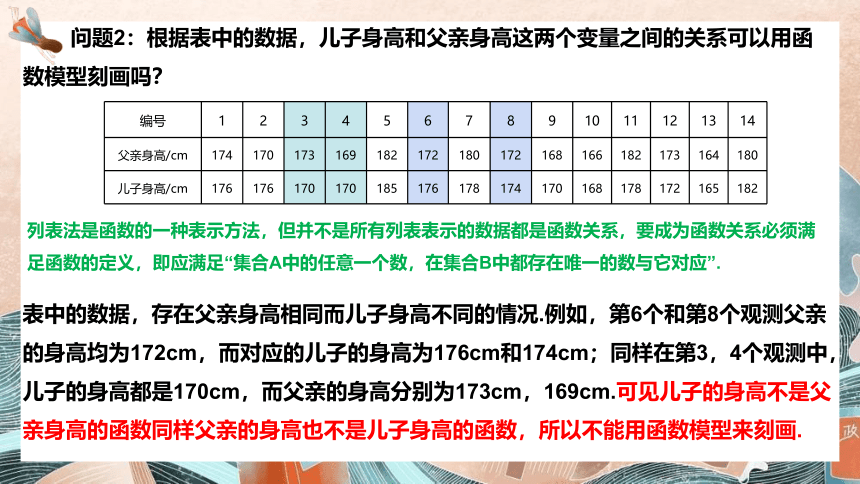
问题2:根据表中的数据,儿子身高和父亲身高这两个变量之间的关系可以用函数模型刻画吗?
列表法是函数的一种表示方法,但并不是所有列表表示的数据都是函数关系,要成为函数关系必须满足函数的定义,即应满足“集合A中的任意一个数,在集合B中都存在唯一的数与它对应”.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
表中的数据,存在父亲身高相同而儿子身高不同的情况.例如,第6个和第8个观测父亲的身高均为172cm,而对应的儿子的身高为176cm和174cm;同样在第3,4个观测中,儿子的身高都是170cm,而父亲的身高分别为173cm,169cm.可见儿子的身高不是父亲身高的函数同样父亲的身高也不是儿子身高的函数,所以不能用函数模型来刻画.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
问题3:从成对样本数据的散点图和样本相关系数可以发现,散点大致分布在一条直线附近表明儿子身高和父亲身高有较强的线性关系.我们可以这样理解,由于有其他因素的存在,使儿子身高和父亲身高有关系但不是函数关系.那么影响儿子身高的其他因素是什么?
影响儿子身高的因素除父亲的身外,还有母亲的身高、生活的环境、饮食习惯、营养水平、体育锻炼等随机的因素,儿子身高是父亲身高的函数的原因是存在这些随机的因素.
问题4:由问题3我们知道,正是因为存在这些随机的因素,使得儿子的身高呈现出随机性各种随机因素都是独立的,有些因素又无法量化.你能否考虑到这些随机因素的作用,用类似于函数的表达式,表示儿子身高与父亲身高的关系吗?
如果用x表示父亲身高,Y表示儿子的身高,用e表示各种其他随机因素影响之和,称e为随机误差,由于儿子身高与父亲身高线性相关,所以Y=bx+a.
Y=bx+a+e.
追问1:为什么要假设E(e)=0,而不假设其为某个不为0的常数?
因为误差是随机的,即取各种正负误差的可能性一样,所以它们均值的理想状态应该为0.
若用x表示父亲身高,Y表示儿子身高,e表示随机误差. 假定随机误差e的均值为0,方差为与父亲身高无关的定值σ2,则它们之间的关系可以表示为
我们称(1)式为Y关于x的一元线性回归模型. 其中,Y称为因变量或响应变量,x称为自变量或解释变量;a和b为模型的未知参数,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差. 模型中的Y也是随机变量,其值虽不能由变量x的值确定,但却能表示为bx+a与e的和,前一部分由x所确定,后一部分是随机的. 如果e=0,那么Y与x之间的关系就可用一元线性函数模型来描述.
你能结合父亲与儿子身高的实例,说明回归模型(1)的意义?
对于父亲身高为xi的某一名男大学生,他的身高yi一定是bxi+a吗?
课堂练习(课本P107)
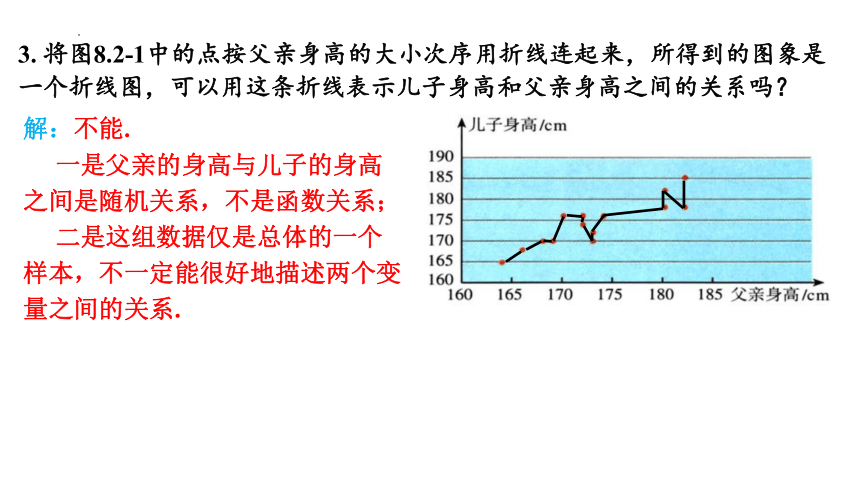
解:不能.
一是父亲的身高与儿子的身高之间是随机关系,不是函数关系;
二是这组数据仅是总体的一个样本,不一定能很好地描述两个变量之间的关系.
3. 将图8.2-1中的点按父亲身高的大小次序用折线连起来,所得到的图象是一个折线图,可以用这条折线表示儿子身高和父亲身高之间的关系吗?
在一元线性回归模型中,表达式Y=bx+a+e刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,需要根据成对样本数据进行估计. 由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
探究 利用散点图找出一条直线,使各散点在整体上与此直线尽可能接近.
方法一:采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置. 然后测量出此时的斜率和截距,就可得到一 条直线,如图(1)所示.
方法二: 在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同,把这条直线作为所求直线,如图(2)所示.
方法三:在散点图中多取几对点,确定出几条直线的方程,再分别求出这些直线的斜率、截距的平均数,将这两个平均数作为所求直线的斜率和截距,如图(3)所示.
上面这些方法虽然有一定的道理,但比较难操作,我们需要另辟蹊径.
先进一步明确我们面临的任务: 从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.
通常,我们会想到利用点到直线y=bx+a的“距离”来刻画散点与该直线的接近程度,然后用所有“距离”之和刻画所有样本观测数据与该直线的接近程度.
设满足一元线性回归模型的两个变量的n对样本数据为(x1, y1), (x2, y2), , (xn, yn), 由yi=bxi+a+ei (i=1, 2, , n),得
显然|ei|越小,表示点(xi , yi)与点(xi , bxi+a)的“距离”越小,即样本数据点离直线y=bx+a的竖直距离越小,如右图所示. 特别地,当ei = 0时,表示点(xi , yi)在这条直线上.
因此,可以用这n个竖直距离之和 来刻画各样本观测数据与直线y=bx+a的“整体接近程度”.
在实际应用中,因为绝对值使得计算不方便,所以人们通常用各散点到直线的竖直距离的平方之和来刻画“整体接近程度”.
求a, b的值,使Q(a, b)最小
残差平方和:
残差:实际值与估计值之间的差值,即
思考:如何求a,b的值,使 最小?
记
注意到
所以
当 取最小值时, 取最小值0,即 .
此时
上式是关于b的二次函数,因此要使Q取得最小值,当且仅当b的取值为
综上,当a,b的取值为 时, Q达到最小.
易得:(1)经验回归直线必过样本中心 ;
(2) 与相关系数r符号相同.
我们将 称为Y 关于x 的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法,求得的 , 叫做b,a的最小二乘估计.
经验回归方程与最小二乘估计:
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
对于上表中的数据,利用公式(2)可以计算出 得到儿子身高Y关于父亲身高x的经验回归方程为 相应的经验回归直线如下图所示.
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
例1 某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1) 画出销售额和利润额的散点图;
(2) 计算利润额y对销售额x的经验回归直线方程.
解:(1) 散点图如下:
∴所求经验回归方程为
解1:(2)
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
∴所求经验回归方程为
解2:(2)
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
求经验回归方程的步骤:
思考1 已知儿子身高关于父亲身高x的经验回归方程为
如果一位父亲的身高为176cm,他儿子长大成人后的身高一定是177cm吗 为什么
显然不一定,因为还有其他影响儿子身高的因素,父亲身高不能完全决定儿子身高. 不过,我们可以作出推测,当父亲身高为176cm时,儿子身高一般在177cm左右.
实际上,如果把这所学校父亲身高为176cm的所有儿子身高作为一个子总体,那么177cm是这个子总体的均值的估计值.
这里的经验回归方程 其斜率可以解释为父亲身高每增加1 cm,其儿子身高平均增加0.839cm. 分析模型还可以发现,高个子父亲有生高个子儿子的趋势,但一群高个子父亲的儿子们的平均身高要低于父亲们的平均身高,例如 x=185(cm),则 =184.172(cm).
矮个子父亲有生矮个子儿子的趋势,但一群矮个子父亲的儿子们的平均身高要高于父亲们的平均身高,例如 x=170(cm),则 =171.587(cm).
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的)称为预测值,观测值减去预测值称为残差. 残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.
残差分析:
例如,对于下表中的第6个观测,父亲身高为172cm,其儿子身高的观测值为y6=176(cm),预测值为 残差为176-173.265=2.735(cm).
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
类似地,我们还可以得到其他的残差,如下表所示.
编号 父亲身高/cm 儿子身高观测值/cm 儿子身高预测值/cm 残差/cm
1 174 176 174.943 1.057
2 170 176 171.587 4.413
3 173 170 174.104 -4.104
4 169 170 170.748 -0.748
5 182 185 181.655 3.345
6 172 176 173.265 2.735
7 180 178 179.977 -1.977
8 172 174 173.265 0.735
9 168 170 169.909 0.091
10 166 168 168.231 -0.231
11 182 178 181.655 -3.655
12 173 172 174.104 -2.104
13 164 165 66.553 -1.553
14 180 182 179.977 2.023
为了使数据更加直观,用父亲身高作为横坐标,残差作为纵坐标,可以画出残差图,如图下所示.
残差图:
0
1
2
3
4
5
-1
-2
-3
-4
-5
160
165
170
175
180
185
残差/cm
父亲身高/cm
观察残差的散点图可以发现,残差比较均匀地分布在横轴的两边. 说明残差比较符合一元线性回归模型的假定,是均值为0、方差为σ2的随机变量的观测值. 可见,通过观察残差图可以直观判断模型是否满足一元线性回归模型的假设.
思考2 观察下列四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定
通过观察发现,图(4)的残差比较均匀地分布在以取值为0的横轴为对称轴的水平带状区域内. 所以在四幅残差图中,只有图(4)满足一元线性回归模型对随机误差的假设.
课堂小结:
1. 经验回归方程:
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线. 这种求经验回归方程的方法叫做最小二乘法.
2. 最小二乘估计:
经验回归方程中的参数 计算公式为:
课堂练习(课本P113)
∴估计女儿的身高为168 cm左右.
2. 假如女儿身高y (单位: cm)关于父亲身高x (单位: cm)的经验回归方程为
已知父亲身高为175 cm,请估计女儿的身高.
解:
解:
5. 假设变量x与变量Y的n对观测数据为(x1, y1),(x2, y2), ,(xn, yn),两个变量满足一元线性回归模型
请写出参数b的最小二乘估计.
则Q是关于b的二次函数. 要使Q小值,当且仅当b的取值为
THANKS
“
”
大本习题讲解
A.变量x,y之间呈负相关关系
B.m=4
C.可以预测,当x=11时,y约为2.6
D.由表格数据知,该经验回归直线必过点(9,4)
ACD
x 6 8 10 12
y 6 M 3 2
故x,y呈负相关关系,则A正确.
解得m=5,B错误.
当x=11时,y的预测值为2.6,故C正确.
例2 某地随着经济的发展,居民收入逐年增长,该地一银行连续五年年底的储蓄存款情况如下表所示.
题型二 求经验回归方程
年份x 2018 2019 2020 2021 2022
储蓄存款额y /千亿元 5 6 7 8 10
为了计算方便,工作人员将上表的数据进行了处理,令t=x-2 017,z=y-5,得到下表.
t 1 2 3 4 5
z 0 1 2 3 5
(1)作z关于t的散点图,求z关于t的经验回归方程;
解 作散点图,直观看z与t具有线性相关关系.
根据z关于t的表格数据,得
(2)通过(1)中的方程,求出y关于x的回归方程.
习题讲解
——分层精练
A.劳动生产率为1 000元时,工人工资为130元
B.劳动生产率提高1 000元时,工人工资平均提高80元
C.劳动生产率提高1 000元时,工人工资平均提高130元
D.当月工资为250元时,劳动生产率为2 000元
B
解析 因为经验回归直线的斜率为80,
所以x每增加1,y平均增加80,
即劳动生产率提高1 000元时,工人工资平均提高80元.
3.在线性回归模型y=bx+a+e中,下列说法正确的是( )
A.y=bx+a+e是一次函数
B.因变量y是由自变量x唯一确定的
C.因变量y除了受自变量x的影响外,可能还受到其它因素的影响,这些因素会导致随机误差e的产生
D.随机误差e是由于计算不准确造成的,可通过精确计算避免随机误差e的产生
C
解析 选项A,在线性回归模型y=bx+a+e中,方程表示的不是函数关系,因此不是一次函数,故A错误;
选项B,因变量y不是由自变量x唯一确定的,故B错误;
选项D,随机误差是不能避免的,只能将误差缩小,但是不能没有误差,故D错误,只有选项C成立.
11.(多选)为研究需要,统计了两个变量x,y的数据情况如表:
x x1 x2 x3 … xn
y y1 y2 y3 … yn
ABD
解析 对于A,因为方差是表示数据波动大小的量,将一组数据的每个数都加一个相同的常数后,方差不变,所以A正确;
对于B,样本相关系数r=-0.8,|r|>0.75,变量x,y的相关性强,所以B正确;
x 2 4 7 10 15 22
y 8.1 9.4 12 14.4 18.5 24
其中,阴历22日是分界线,从阴历22日开始月亮就要到第二天(即23日0:00)才升起.则( )
A.经验回归直线过点(10,14.4)
C.预测月出时间为16时的那天是阴历13日
D.预测阴历27日的月出时间为阴历28日早上4:00
故经验回归直线过点(10,14.4),选项A正确;
AD
∴月出时间为阴历12日,选项C错误;
∴日出时间应该为28日早上4:00,选项D正确.
8.2.1一元线性回归模型及其参数的最小二乘估计
人教A版2019必修第三册
1. 样本相关系数:
2.相关系数的性质:
① 当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关.
② |r|≤1;
③ 当|r|越接近1时,成对数据的线性相关程度越强;当|r|越接近0时,成对数据的线性相关程度越弱;特别地,当|r|=0时,成对数据的没有线性相关关系;当|r|=1时,成对数据都落在一条直线上.
通过前面的学习我们已经了解到,根据成对样本数据的散点图和样本相关系数,可以推断两个变量是否存在相关关系、是正相关还是负相关,以及线性相关程度的强弱等. 进一步地,如果能像建立函数模型刻画两个变量之间的确定性关系那样,通过建立适当的统计模型刻画两个随机变量的相关关系,那么我们就可以利用这个模型研究两个变量之间的随机关系,并通过模型进行预测.
下面我们研究当两个变量线性相关时,如何利用成对样本数据建立统计模型,并利用模型进行预测的问题.
问题1:生活经验告诉我们,儿子的身高与父亲的身高相关.一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如表1所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
可以发现,散点大致分布在一条从左下角到右上角的直线附近,表明儿子身高和父亲身高线性相关.利用统计软件,求得样本相关系数为r≈0.886,表明儿子身高和父亲身高正线性相关,且相关程度较高。
问题2:根据表中的数据,儿子身高和父亲身高这两个变量之间的关系可以用函数模型刻画吗?
列表法是函数的一种表示方法,但并不是所有列表表示的数据都是函数关系,要成为函数关系必须满足函数的定义,即应满足“集合A中的任意一个数,在集合B中都存在唯一的数与它对应”.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
表中的数据,存在父亲身高相同而儿子身高不同的情况.例如,第6个和第8个观测父亲的身高均为172cm,而对应的儿子的身高为176cm和174cm;同样在第3,4个观测中,儿子的身高都是170cm,而父亲的身高分别为173cm,169cm.可见儿子的身高不是父亲身高的函数同样父亲的身高也不是儿子身高的函数,所以不能用函数模型来刻画.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
问题3:从成对样本数据的散点图和样本相关系数可以发现,散点大致分布在一条直线附近表明儿子身高和父亲身高有较强的线性关系.我们可以这样理解,由于有其他因素的存在,使儿子身高和父亲身高有关系但不是函数关系.那么影响儿子身高的其他因素是什么?
影响儿子身高的因素除父亲的身外,还有母亲的身高、生活的环境、饮食习惯、营养水平、体育锻炼等随机的因素,儿子身高是父亲身高的函数的原因是存在这些随机的因素.
问题4:由问题3我们知道,正是因为存在这些随机的因素,使得儿子的身高呈现出随机性各种随机因素都是独立的,有些因素又无法量化.你能否考虑到这些随机因素的作用,用类似于函数的表达式,表示儿子身高与父亲身高的关系吗?
如果用x表示父亲身高,Y表示儿子的身高,用e表示各种其他随机因素影响之和,称e为随机误差,由于儿子身高与父亲身高线性相关,所以Y=bx+a.
Y=bx+a+e.
追问1:为什么要假设E(e)=0,而不假设其为某个不为0的常数?
因为误差是随机的,即取各种正负误差的可能性一样,所以它们均值的理想状态应该为0.
若用x表示父亲身高,Y表示儿子身高,e表示随机误差. 假定随机误差e的均值为0,方差为与父亲身高无关的定值σ2,则它们之间的关系可以表示为
我们称(1)式为Y关于x的一元线性回归模型. 其中,Y称为因变量或响应变量,x称为自变量或解释变量;a和b为模型的未知参数,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差. 模型中的Y也是随机变量,其值虽不能由变量x的值确定,但却能表示为bx+a与e的和,前一部分由x所确定,后一部分是随机的. 如果e=0,那么Y与x之间的关系就可用一元线性函数模型来描述.
你能结合父亲与儿子身高的实例,说明回归模型(1)的意义?
对于父亲身高为xi的某一名男大学生,他的身高yi一定是bxi+a吗?
课堂练习(课本P107)
解:不能.
一是父亲的身高与儿子的身高之间是随机关系,不是函数关系;
二是这组数据仅是总体的一个样本,不一定能很好地描述两个变量之间的关系.
3. 将图8.2-1中的点按父亲身高的大小次序用折线连起来,所得到的图象是一个折线图,可以用这条折线表示儿子身高和父亲身高之间的关系吗?
在一元线性回归模型中,表达式Y=bx+a+e刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,需要根据成对样本数据进行估计. 由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
探究 利用散点图找出一条直线,使各散点在整体上与此直线尽可能接近.
方法一:采用测量的方法,先画出一条直线,测量出各点与它的距离,然后移动直线,到达一个使距离的和最小的位置. 然后测量出此时的斜率和截距,就可得到一 条直线,如图(1)所示.
方法二: 在图中选择这样的两点画直线,使得直线两侧的点的个数基本相同,把这条直线作为所求直线,如图(2)所示.
方法三:在散点图中多取几对点,确定出几条直线的方程,再分别求出这些直线的斜率、截距的平均数,将这两个平均数作为所求直线的斜率和截距,如图(3)所示.
上面这些方法虽然有一定的道理,但比较难操作,我们需要另辟蹊径.
先进一步明确我们面临的任务: 从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.
通常,我们会想到利用点到直线y=bx+a的“距离”来刻画散点与该直线的接近程度,然后用所有“距离”之和刻画所有样本观测数据与该直线的接近程度.
设满足一元线性回归模型的两个变量的n对样本数据为(x1, y1), (x2, y2), , (xn, yn), 由yi=bxi+a+ei (i=1, 2, , n),得
显然|ei|越小,表示点(xi , yi)与点(xi , bxi+a)的“距离”越小,即样本数据点离直线y=bx+a的竖直距离越小,如右图所示. 特别地,当ei = 0时,表示点(xi , yi)在这条直线上.
因此,可以用这n个竖直距离之和 来刻画各样本观测数据与直线y=bx+a的“整体接近程度”.
在实际应用中,因为绝对值使得计算不方便,所以人们通常用各散点到直线的竖直距离的平方之和来刻画“整体接近程度”.
求a, b的值,使Q(a, b)最小
残差平方和:
残差:实际值与估计值之间的差值,即
思考:如何求a,b的值,使 最小?
记
注意到
所以
当 取最小值时, 取最小值0,即 .
此时
上式是关于b的二次函数,因此要使Q取得最小值,当且仅当b的取值为
综上,当a,b的取值为 时, Q达到最小.
易得:(1)经验回归直线必过样本中心 ;
(2) 与相关系数r符号相同.
我们将 称为Y 关于x 的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法,求得的 , 叫做b,a的最小二乘估计.
经验回归方程与最小二乘估计:
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
对于上表中的数据,利用公式(2)可以计算出 得到儿子身高Y关于父亲身高x的经验回归方程为 相应的经验回归直线如下图所示.
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
例1 某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1) 画出销售额和利润额的散点图;
(2) 计算利润额y对销售额x的经验回归直线方程.
解:(1) 散点图如下:
∴所求经验回归方程为
解1:(2)
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
∴所求经验回归方程为
解2:(2)
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
求经验回归方程的步骤:
思考1 已知儿子身高关于父亲身高x的经验回归方程为
如果一位父亲的身高为176cm,他儿子长大成人后的身高一定是177cm吗 为什么
显然不一定,因为还有其他影响儿子身高的因素,父亲身高不能完全决定儿子身高. 不过,我们可以作出推测,当父亲身高为176cm时,儿子身高一般在177cm左右.
实际上,如果把这所学校父亲身高为176cm的所有儿子身高作为一个子总体,那么177cm是这个子总体的均值的估计值.
这里的经验回归方程 其斜率可以解释为父亲身高每增加1 cm,其儿子身高平均增加0.839cm. 分析模型还可以发现,高个子父亲有生高个子儿子的趋势,但一群高个子父亲的儿子们的平均身高要低于父亲们的平均身高,例如 x=185(cm),则 =184.172(cm).
矮个子父亲有生矮个子儿子的趋势,但一群矮个子父亲的儿子们的平均身高要高于父亲们的平均身高,例如 x=170(cm),则 =171.587(cm).
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的)称为预测值,观测值减去预测值称为残差. 残差是随机误差的估计结果,通过对残差的分析可以判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.
残差分析:
例如,对于下表中的第6个观测,父亲身高为172cm,其儿子身高的观测值为y6=176(cm),预测值为 残差为176-173.265=2.735(cm).
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
类似地,我们还可以得到其他的残差,如下表所示.
编号 父亲身高/cm 儿子身高观测值/cm 儿子身高预测值/cm 残差/cm
1 174 176 174.943 1.057
2 170 176 171.587 4.413
3 173 170 174.104 -4.104
4 169 170 170.748 -0.748
5 182 185 181.655 3.345
6 172 176 173.265 2.735
7 180 178 179.977 -1.977
8 172 174 173.265 0.735
9 168 170 169.909 0.091
10 166 168 168.231 -0.231
11 182 178 181.655 -3.655
12 173 172 174.104 -2.104
13 164 165 66.553 -1.553
14 180 182 179.977 2.023
为了使数据更加直观,用父亲身高作为横坐标,残差作为纵坐标,可以画出残差图,如图下所示.
残差图:
0
1
2
3
4
5
-1
-2
-3
-4
-5
160
165
170
175
180
185
残差/cm
父亲身高/cm
观察残差的散点图可以发现,残差比较均匀地分布在横轴的两边. 说明残差比较符合一元线性回归模型的假定,是均值为0、方差为σ2的随机变量的观测值. 可见,通过观察残差图可以直观判断模型是否满足一元线性回归模型的假设.
思考2 观察下列四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定
通过观察发现,图(4)的残差比较均匀地分布在以取值为0的横轴为对称轴的水平带状区域内. 所以在四幅残差图中,只有图(4)满足一元线性回归模型对随机误差的假设.
课堂小结:
1. 经验回归方程:
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线. 这种求经验回归方程的方法叫做最小二乘法.
2. 最小二乘估计:
经验回归方程中的参数 计算公式为:
课堂练习(课本P113)
∴估计女儿的身高为168 cm左右.
2. 假如女儿身高y (单位: cm)关于父亲身高x (单位: cm)的经验回归方程为
已知父亲身高为175 cm,请估计女儿的身高.
解:
解:
5. 假设变量x与变量Y的n对观测数据为(x1, y1),(x2, y2), ,(xn, yn),两个变量满足一元线性回归模型
请写出参数b的最小二乘估计.
则Q是关于b的二次函数. 要使Q小值,当且仅当b的取值为
THANKS
“
”
大本习题讲解
A.变量x,y之间呈负相关关系
B.m=4
C.可以预测,当x=11时,y约为2.6
D.由表格数据知,该经验回归直线必过点(9,4)
ACD
x 6 8 10 12
y 6 M 3 2
故x,y呈负相关关系,则A正确.
解得m=5,B错误.
当x=11时,y的预测值为2.6,故C正确.
例2 某地随着经济的发展,居民收入逐年增长,该地一银行连续五年年底的储蓄存款情况如下表所示.
题型二 求经验回归方程
年份x 2018 2019 2020 2021 2022
储蓄存款额y /千亿元 5 6 7 8 10
为了计算方便,工作人员将上表的数据进行了处理,令t=x-2 017,z=y-5,得到下表.
t 1 2 3 4 5
z 0 1 2 3 5
(1)作z关于t的散点图,求z关于t的经验回归方程;
解 作散点图,直观看z与t具有线性相关关系.
根据z关于t的表格数据,得
(2)通过(1)中的方程,求出y关于x的回归方程.
习题讲解
——分层精练
A.劳动生产率为1 000元时,工人工资为130元
B.劳动生产率提高1 000元时,工人工资平均提高80元
C.劳动生产率提高1 000元时,工人工资平均提高130元
D.当月工资为250元时,劳动生产率为2 000元
B
解析 因为经验回归直线的斜率为80,
所以x每增加1,y平均增加80,
即劳动生产率提高1 000元时,工人工资平均提高80元.
3.在线性回归模型y=bx+a+e中,下列说法正确的是( )
A.y=bx+a+e是一次函数
B.因变量y是由自变量x唯一确定的
C.因变量y除了受自变量x的影响外,可能还受到其它因素的影响,这些因素会导致随机误差e的产生
D.随机误差e是由于计算不准确造成的,可通过精确计算避免随机误差e的产生
C
解析 选项A,在线性回归模型y=bx+a+e中,方程表示的不是函数关系,因此不是一次函数,故A错误;
选项B,因变量y不是由自变量x唯一确定的,故B错误;
选项D,随机误差是不能避免的,只能将误差缩小,但是不能没有误差,故D错误,只有选项C成立.
11.(多选)为研究需要,统计了两个变量x,y的数据情况如表:
x x1 x2 x3 … xn
y y1 y2 y3 … yn
ABD
解析 对于A,因为方差是表示数据波动大小的量,将一组数据的每个数都加一个相同的常数后,方差不变,所以A正确;
对于B,样本相关系数r=-0.8,|r|>0.75,变量x,y的相关性强,所以B正确;
x 2 4 7 10 15 22
y 8.1 9.4 12 14.4 18.5 24
其中,阴历22日是分界线,从阴历22日开始月亮就要到第二天(即23日0:00)才升起.则( )
A.经验回归直线过点(10,14.4)
C.预测月出时间为16时的那天是阴历13日
D.预测阴历27日的月出时间为阴历28日早上4:00
故经验回归直线过点(10,14.4),选项A正确;
AD
∴月出时间为阴历12日,选项C错误;
∴日出时间应该为28日早上4:00,选项D正确.
