9.1.2三角形的内角和与外角和 教案
文档属性
| 名称 | 9.1.2三角形的内角和与外角和 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 09:50:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.1.2三角形的内角和与外角和 教学设计
课题 9.1.2三角形的内角和与外角和 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 小学阶段已经了解了“三角形的内角和等于180°”,但是,教材又将学生熟悉的知识点安排在此处,不仅仅是为了让学生做简单的回顾,更主要的是要让学生学习用演绎推理的方法证明这个结论.并在这个结论的基础上推出:直角三角形的两个锐角互余;三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,最后再给出“三角形的外角和等于360°”的结论,作为对后面探索多边形的外角和定理的铺垫.这部分内容是让学生进行演绎推理很好的素材,并且让学生体会到数学证明的必要性.
核心素养分析 通过剪拼的实验与操作,提高动手能力.经历三角形内角和外角关系的探究过程,在探究中发展合情推理的能力.使学生学会探索数学问题的归纳法和实验法等研究方法.
学习目标 1.理解三角形的外角的两条性质以及三角形的内角和与外角和.2.会利用“三角形的一个外角等于和它不相邻的两个内角的和”进行有关计算.
重点 理解并掌握三角形外角的性质以及其外角的和.
难点 三角形内角和外角的计算.
教学过程
教学环节 教师活动 学生活动 设计意图
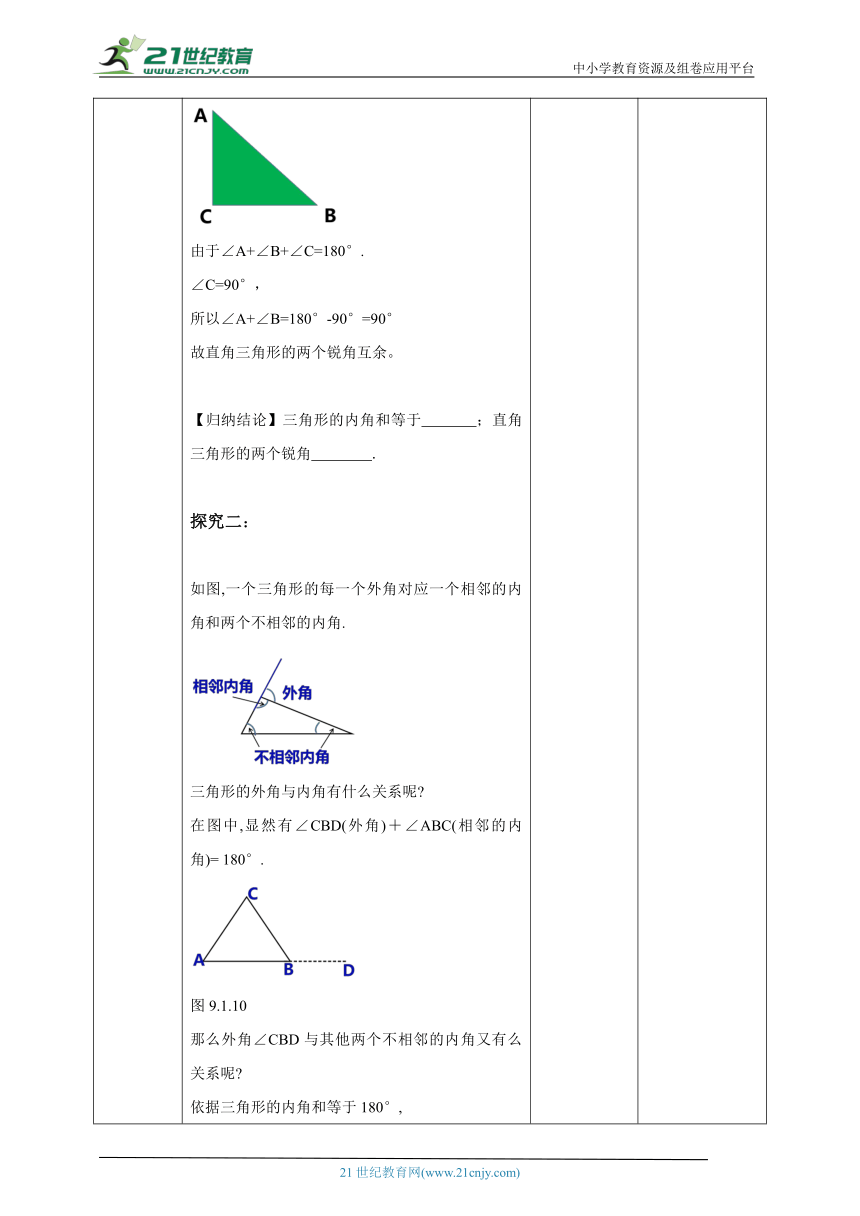
导入新课 一、创设情景,引出课题在小学里,学生知道三角形内角和等于1800 ,通过运用几何画版制作的课件,使学生直观地感受三角形的三个内角之间的关系。情境1:感受△ABC的形状在不断变化过程中三角形三内角的和为1800。情境2:感受△ABC用拼图的方法得出三角形内角和等于1800 。方法一,在△ABC中,把∠A撕下,然后把点A与点C重合在同一点,摆成如图所示的位置。方法二,其它拼图验证方法(如集中在A点)得出如下的结论:三角形的内角和等于180°.如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?探究一:如图,已知△ABC,分别用∠1、∠2、∠3表示ABC的三个内角,证明∠1+∠2+∠3=180°.解 延长BC至点E,以点C为顶点,在BE的上侧作∠DCE =∠2 ,则CD// BA(同位角相等,两直线平行).∵CD// BA,∴∠1 = ∠ACD(两直线平行,内错角相等)∵∠3 + ∠ACD+ ∠DCE =180°,∴∠1 +∠2 +∠3 =180°(等量代换).由三角形的内角和等于180°,容易得出下面的结论:直角三角形的两个锐角互余.由于∠A+∠B+∠C=180°.∠C=90°,所以∠A+∠B=180°-90°=90°故直角三角形的两个锐角互余。【归纳结论】三角形的内角和等于 ;直角三角形的两个锐角 .探究二:如图,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.三角形的外角与内角有什么关系呢 在图中,显然有∠CBD(外角)+∠ABC(相邻的内角)= 180°.图9.1.10那么外角∠CBD与其他两个不相邻的内角又有么关系呢 依据三角形的内角和等于180°,我们有∠ACB +∠BAC + ∠ABC = 180°.由上面两个式子,可以推出∠CBD = 180° - ∠ABC,∠ACB +∠BAC =180° -∠ABC.因而可以得到你与你的同伴所发现的结论:∠CBD =∠ACB +∠BAC.由此可知,三角形的外角有两条性质:1.三角形的一个外角等于与它不相邻的两个内角的和.2.三角形的一个外角大于任何一个与它不相邻的内角.与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.如图9.1.11所示,∠1 +∠2 +∠3就是△ABC的外角和.做一做在图9.1.11中,∠1+_______= 180°,∠2 +_______=180°,∠3 +_______=180°.三式相加可以得到∠1 +∠2 +∠3+_______+_______+_______=_______①而∠ACB +∠BAC +∠ABC =180°,②将①与②相比较,你能得出什么结论 可以得到∠1 +∠2 +∠3 = 360°.由此可知:三角形的外角和等于360°.你能由下图说明这一结论吗? ∠2+∠EAD+∠BAD=360°∵∠EAD=∠1, ∠BAD=∠3∴∠2+∠1+∠3=360° 思考自议引入新课,激发学生继续探究三角形内角和和外角和的兴趣。
培养学生的数学语言表达能力,培养逻辑推理能力。
讲授新课 提炼概念三角形的内角和定理文字语言:三角形的内角和等于180°符号语言:∵ ∠A、∠B、∠C是△ABC的三个内角∴ ∠A+∠B+∠C=180°(三角形的内角和等180°)三角形外角的性质∠ACD=∠ABC+ ∠BAC 即:三角形的一个外角等于与它不相邻的两个内角的和.因为:∠ACD+∠ACB=180° ∠ABC+ ∠BAC+ ∠ACB=180 °可知:三角形的一个外角大于任何一个与它不相邻的内角.典例精讲例1 如图9.1.12,D是ABC的BC边上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.求:(1) ∠B的度数;(2)∠C的度数.解(1)∵∠ADC是△ABD的外角(已知),∴∠B +∠BAD = ∠ADC = 80°(三角形的一个外角等于与它不相邻的两个内角的和).又∵ ∠B =∠BAD(已知), ∴∠B =80°× = 40°(等量代换).(2)∵∠B +∠BAC+∠C = 180°(三角形的内角和等于180°),∴∠C = 180° -∠B -∠BAC(等式的性质)= 180° -40° -70°= 70°. 掌握三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,三角形的外角和等于360°。 总结三角形内角和和外角和,引入新课,鼓励学生探索新知。
课堂练习 四、巩固训练 1.将一副三角板按如图方式重叠,则∠1的度数为( )A.45° B.60° C.75° D.105°C2.判断∠1与∠3的大小,并说明理由。解:∠3 > ∠1∵∠3 >∠2 ,∠2 >∠1∴∠3 >∠13.如图所示:求∠A+∠B+∠C+∠D+∠E的度数?解:∵∠1= ∠A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又∵∠2= ∠B+ ∠E(三角形的外角等于与它不相邻的两内角的和)∴ ∠A+∠B+∠C+∠D+∠E=(∠A+ ∠D)+(∠B+ ∠E)+∠C=∠1+∠2+∠C=180°4.如图,D是△ABC中的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.解:设∠1=∠2=x°,∵∠4是△ABD的外角,∴∠4=∠3=∠1+∠2=2x°,又∵∠BAC+∠3+∠2=180°,∴66°+2x°+x°=180°,∴x°=38°,∴∠DAC=∠BAC-∠1=66°-38°=28°
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
9.1.2三角形的内角和与外角和 教学设计
课题 9.1.2三角形的内角和与外角和 单元 第9 单元 学科 数学 年级 七年级(下)
教材分析 小学阶段已经了解了“三角形的内角和等于180°”,但是,教材又将学生熟悉的知识点安排在此处,不仅仅是为了让学生做简单的回顾,更主要的是要让学生学习用演绎推理的方法证明这个结论.并在这个结论的基础上推出:直角三角形的两个锐角互余;三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,最后再给出“三角形的外角和等于360°”的结论,作为对后面探索多边形的外角和定理的铺垫.这部分内容是让学生进行演绎推理很好的素材,并且让学生体会到数学证明的必要性.
核心素养分析 通过剪拼的实验与操作,提高动手能力.经历三角形内角和外角关系的探究过程,在探究中发展合情推理的能力.使学生学会探索数学问题的归纳法和实验法等研究方法.
学习目标 1.理解三角形的外角的两条性质以及三角形的内角和与外角和.2.会利用“三角形的一个外角等于和它不相邻的两个内角的和”进行有关计算.
重点 理解并掌握三角形外角的性质以及其外角的和.
难点 三角形内角和外角的计算.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 一、创设情景,引出课题在小学里,学生知道三角形内角和等于1800 ,通过运用几何画版制作的课件,使学生直观地感受三角形的三个内角之间的关系。情境1:感受△ABC的形状在不断变化过程中三角形三内角的和为1800。情境2:感受△ABC用拼图的方法得出三角形内角和等于1800 。方法一,在△ABC中,把∠A撕下,然后把点A与点C重合在同一点,摆成如图所示的位置。方法二,其它拼图验证方法(如集中在A点)得出如下的结论:三角形的内角和等于180°.如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?探究一:如图,已知△ABC,分别用∠1、∠2、∠3表示ABC的三个内角,证明∠1+∠2+∠3=180°.解 延长BC至点E,以点C为顶点,在BE的上侧作∠DCE =∠2 ,则CD// BA(同位角相等,两直线平行).∵CD// BA,∴∠1 = ∠ACD(两直线平行,内错角相等)∵∠3 + ∠ACD+ ∠DCE =180°,∴∠1 +∠2 +∠3 =180°(等量代换).由三角形的内角和等于180°,容易得出下面的结论:直角三角形的两个锐角互余.由于∠A+∠B+∠C=180°.∠C=90°,所以∠A+∠B=180°-90°=90°故直角三角形的两个锐角互余。【归纳结论】三角形的内角和等于 ;直角三角形的两个锐角 .探究二:如图,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.三角形的外角与内角有什么关系呢 在图中,显然有∠CBD(外角)+∠ABC(相邻的内角)= 180°.图9.1.10那么外角∠CBD与其他两个不相邻的内角又有么关系呢 依据三角形的内角和等于180°,我们有∠ACB +∠BAC + ∠ABC = 180°.由上面两个式子,可以推出∠CBD = 180° - ∠ABC,∠ACB +∠BAC =180° -∠ABC.因而可以得到你与你的同伴所发现的结论:∠CBD =∠ACB +∠BAC.由此可知,三角形的外角有两条性质:1.三角形的一个外角等于与它不相邻的两个内角的和.2.三角形的一个外角大于任何一个与它不相邻的内角.与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角.从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.如图9.1.11所示,∠1 +∠2 +∠3就是△ABC的外角和.做一做在图9.1.11中,∠1+_______= 180°,∠2 +_______=180°,∠3 +_______=180°.三式相加可以得到∠1 +∠2 +∠3+_______+_______+_______=_______①而∠ACB +∠BAC +∠ABC =180°,②将①与②相比较,你能得出什么结论 可以得到∠1 +∠2 +∠3 = 360°.由此可知:三角形的外角和等于360°.你能由下图说明这一结论吗? ∠2+∠EAD+∠BAD=360°∵∠EAD=∠1, ∠BAD=∠3∴∠2+∠1+∠3=360° 思考自议引入新课,激发学生继续探究三角形内角和和外角和的兴趣。
培养学生的数学语言表达能力,培养逻辑推理能力。
讲授新课 提炼概念三角形的内角和定理文字语言:三角形的内角和等于180°符号语言:∵ ∠A、∠B、∠C是△ABC的三个内角∴ ∠A+∠B+∠C=180°(三角形的内角和等180°)三角形外角的性质∠ACD=∠ABC+ ∠BAC 即:三角形的一个外角等于与它不相邻的两个内角的和.因为:∠ACD+∠ACB=180° ∠ABC+ ∠BAC+ ∠ACB=180 °可知:三角形的一个外角大于任何一个与它不相邻的内角.典例精讲例1 如图9.1.12,D是ABC的BC边上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.求:(1) ∠B的度数;(2)∠C的度数.解(1)∵∠ADC是△ABD的外角(已知),∴∠B +∠BAD = ∠ADC = 80°(三角形的一个外角等于与它不相邻的两个内角的和).又∵ ∠B =∠BAD(已知), ∴∠B =80°× = 40°(等量代换).(2)∵∠B +∠BAC+∠C = 180°(三角形的内角和等于180°),∴∠C = 180° -∠B -∠BAC(等式的性质)= 180° -40° -70°= 70°. 掌握三角形的一个外角等于与它不相邻的两个内角和;三角形的一个外角大于任何一个与它不相邻的内角,三角形的外角和等于360°。 总结三角形内角和和外角和,引入新课,鼓励学生探索新知。
课堂练习 四、巩固训练 1.将一副三角板按如图方式重叠,则∠1的度数为( )A.45° B.60° C.75° D.105°C2.判断∠1与∠3的大小,并说明理由。解:∠3 > ∠1∵∠3 >∠2 ,∠2 >∠1∴∠3 >∠13.如图所示:求∠A+∠B+∠C+∠D+∠E的度数?解:∵∠1= ∠A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又∵∠2= ∠B+ ∠E(三角形的外角等于与它不相邻的两内角的和)∴ ∠A+∠B+∠C+∠D+∠E=(∠A+ ∠D)+(∠B+ ∠E)+∠C=∠1+∠2+∠C=180°4.如图,D是△ABC中的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.解:设∠1=∠2=x°,∵∠4是△ABD的外角,∴∠4=∠3=∠1+∠2=2x°,又∵∠BAC+∠3+∠2=180°,∴66°+2x°+x°=180°,∴x°=38°,∴∠DAC=∠BAC-∠1=66°-38°=28°
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
