9.1.2三角形的内角和与外角和 课件(共28张PPT)
文档属性
| 名称 | 9.1.2三角形的内角和与外角和 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 10:00:44 | ||
图片预览




文档简介
(共28张PPT)
9.1.2三角形的内角和与外角和
华师大版 七年级 下册
教学目标
教学目标:1.掌握三角形的内角和定理、三角形外角的性质,理解直角三
角形的两个锐角互余的性质.
2.会用三角形的内角与外角的性质来进行相关计算或比较.
教学重点:理解并掌握三角形外角的性质以及其外角的和.
教学难点:三角形内角和外角的计算.
新知导入
情境引入
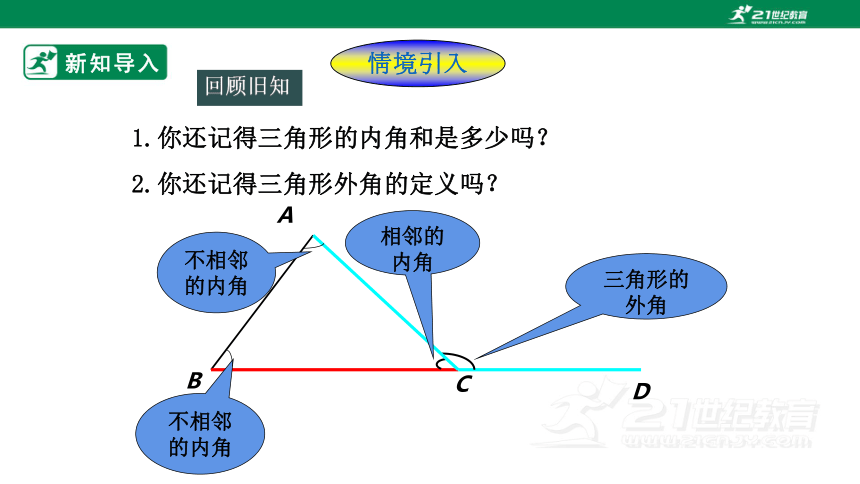
回顾旧知
A
B
C
D
相邻的
内角
三角形的外角
2.你还记得三角形外角的定义吗?
不相邻的内角
不相邻的内角
1.你还记得三角形的内角和是多少吗?
新知讲解
合作学习
你有什么办法可以验证它呢
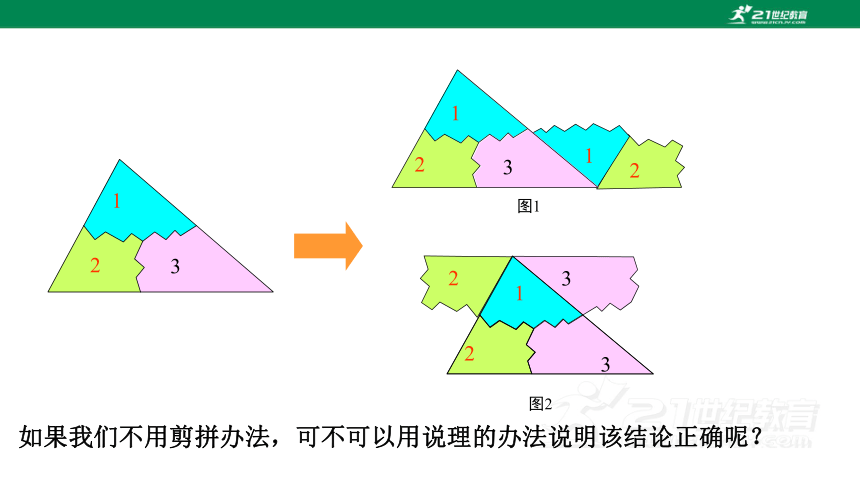
方法一:剪拼法.把三个角拼在一起试试看?
探索1.三角形的内角和.
1
2
3
2
1
图1
1
2
3
2
3
图2
2
3
1
如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?
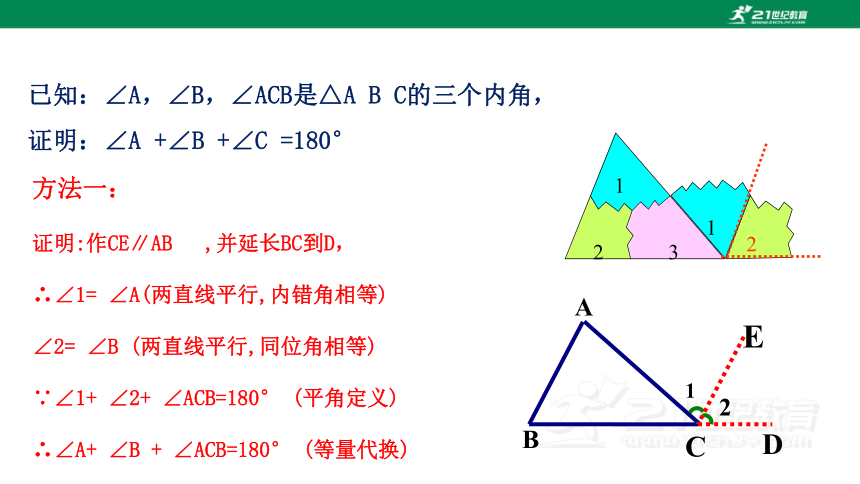
方法一:
证明:作CE∥AB ,并延长BC到D,
∴∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
∵∠1+ ∠2+ ∠ACB=180° (平角定义)
∴∠A+ ∠B + ∠ACB=180° (等量代换)
2
1
2
3
1
已知:∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
2
1
E
D
C
B
A
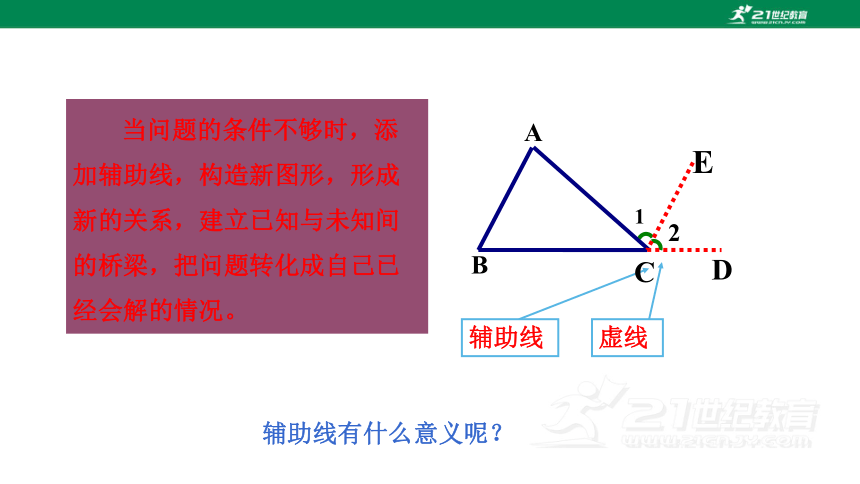
辅助线
辅助线有什么意义呢?
虚线
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
2
1
E
D
C
B
A
F
2
1
E
C
B
A
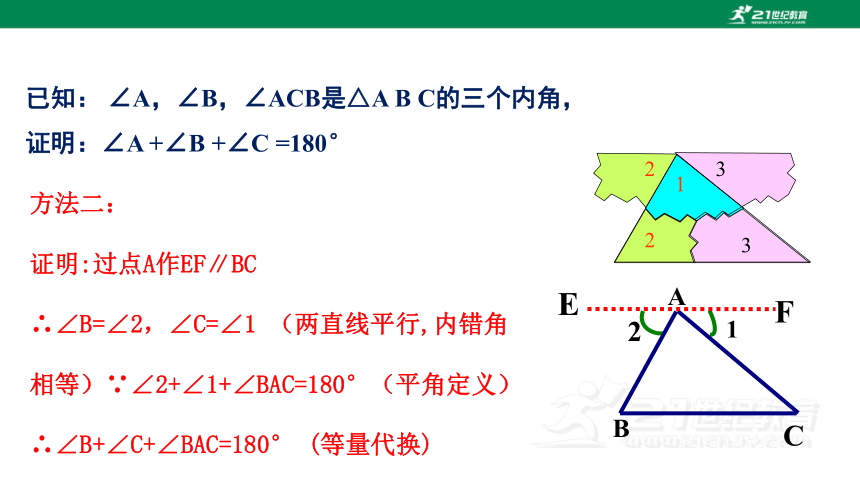
方法二:
证明:过点A作EF∥BC
∴∠B=∠2,∠C=∠1 (两直线平行,内错角相等)∵∠2+∠1+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180° (等量代换)
已知: ∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
1
2
3
3
2
提炼概念
三角形的内角和定理
文字语言:三角形的内角和等于180°
符号语言:
∵ ∠A、∠B、∠C是△ABC的三个内角
∴ ∠A+∠B+∠C=180°(三角形的内角和等180°)
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
想一想
在△ABC 中,若∠C =90°,你能求出∠A,∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?利用上面的结果,你能得出什么结论?
A
B
C
直角三角形的两个锐角互余.
应用格式:
在直角△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC
三角形内外角有什么关系呢?
B
C
D
A
很显然:∠ACD(外角)+∠ACB(内角)=180°
那么外角 ∠ACD与其他两个不相邻的内角又有什么关系呢?
探索2:三角形的外角与内角有什么关系呢?
想一想
B
C
A
D
把 ∠ABC和 ∠BAC分别移动,放到 ∠ACD上,会出现什么结果呢?
发现:∠ACD=∠ABC+ ∠BAC
归纳总结
∠ACD=∠ABC+ ∠BAC
即:三角形的一个外角等于与它不相邻的两个内角的和.
可知:三角形的一个外角大于任何一个与它不相邻的内角.
因为:∠ACD+∠ACB=180°
∠ABC+ ∠BAC+ ∠ACB=180 °
三角形外角的性质
探究新知
B
C
A
)
)
1
2
3
)
与三角形的每个内角相邻的外角分别有两个, 这两个外角是对顶角, 因此取其一作为三角形的外角.
那么∠1+ ∠2+ ∠3就是△ABC的外角和.
)
做一做
所以:∠1+ ∠2+ ∠3= 360 °
∠1+ = 180 °
∠2+ = 180 °
∠3+ = 180 °
三式相加可以得到
∠1+ ∠2+ ∠3+ + + = .
∠ACB
∠BAC
∠ABC
∠ACB
∠BAC
∠ABC
540 °
而 ∠ACB +∠BAC +∠ABC= 180 °
归纳总结
三角形的外角和等于360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
典例精讲
例:D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°∠BAC=70°
求:
(1)∠B的度数(2)∠C的度数
解:(1)∵∠ADC是△ABD的外角(已知)
∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等于与它不相邻的两个内角之和)
又∵∠B=∠BAD(已知)
∴∠B=80° =40°(等量代换)
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)
∴∠C=180°-∠B-∠BAC(等式的性质)
=180°-40°-70°
=70°
归纳概念
总结: 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
课堂练习
1.将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
C
2.判断∠1与∠3的大小,并说明理由。
∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1
解:∠3 > ∠1
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
(三角形的外角等于与它不相邻的两内角的和)
∴ ∠A+∠B+∠C+∠D+∠E
=(∠A+ ∠D)+(∠B+ ∠E)+∠C
=∠1+∠2+∠C=180°
3.如图所示:求∠A+∠B+∠C+∠D+∠E的度数?
4.如图,D是△ABC中的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
解:设∠1=∠2=x°,∵∠4是△ABD的外角,∴∠4=∠3=∠1+∠2=2x°,
又∵∠BAC+∠3+∠2=180°,∴66°+2x°+x°=180°,∴x°=38°,∴∠DAC=∠BAC-∠1=66°-38°=28°
课堂总结
三角形内角和与外角和
三角形的
内角和
三角形内角和等于180 °
直角三角形的两锐角互余
三角形外角和
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
9.1.2三角形的内角和与外角和
华师大版 七年级 下册
教学目标
教学目标:1.掌握三角形的内角和定理、三角形外角的性质,理解直角三
角形的两个锐角互余的性质.
2.会用三角形的内角与外角的性质来进行相关计算或比较.
教学重点:理解并掌握三角形外角的性质以及其外角的和.
教学难点:三角形内角和外角的计算.
新知导入
情境引入
回顾旧知
A
B
C
D
相邻的
内角
三角形的外角
2.你还记得三角形外角的定义吗?
不相邻的内角
不相邻的内角
1.你还记得三角形的内角和是多少吗?
新知讲解
合作学习
你有什么办法可以验证它呢
方法一:剪拼法.把三个角拼在一起试试看?
探索1.三角形的内角和.
1
2
3
2
1
图1
1
2
3
2
3
图2
2
3
1
如果我们不用剪拼办法,可不可以用说理的办法说明该结论正确呢?
方法一:
证明:作CE∥AB ,并延长BC到D,
∴∠1= ∠A(两直线平行,内错角相等)
∠2= ∠B (两直线平行,同位角相等)
∵∠1+ ∠2+ ∠ACB=180° (平角定义)
∴∠A+ ∠B + ∠ACB=180° (等量代换)
2
1
2
3
1
已知:∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
2
1
E
D
C
B
A
辅助线
辅助线有什么意义呢?
虚线
当问题的条件不够时,添加辅助线,构造新图形,形成新的关系,建立已知与未知间的桥梁,把问题转化成自己已经会解的情况。
2
1
E
D
C
B
A
F
2
1
E
C
B
A
方法二:
证明:过点A作EF∥BC
∴∠B=∠2,∠C=∠1 (两直线平行,内错角相等)∵∠2+∠1+∠BAC=180°(平角定义)
∴∠B+∠C+∠BAC=180° (等量代换)
已知: ∠A,∠B,∠ACB是△A B C的三个内角,
证明:∠A +∠B +∠C =180°
1
2
3
3
2
提炼概念
三角形的内角和定理
文字语言:三角形的内角和等于180°
符号语言:
∵ ∠A、∠B、∠C是△ABC的三个内角
∴ ∠A+∠B+∠C=180°(三角形的内角和等180°)
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
想一想
在△ABC 中,若∠C =90°,你能求出∠A,∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?利用上面的结果,你能得出什么结论?
A
B
C
直角三角形的两个锐角互余.
应用格式:
在直角△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC
三角形内外角有什么关系呢?
B
C
D
A
很显然:∠ACD(外角)+∠ACB(内角)=180°
那么外角 ∠ACD与其他两个不相邻的内角又有什么关系呢?
探索2:三角形的外角与内角有什么关系呢?
想一想
B
C
A
D
把 ∠ABC和 ∠BAC分别移动,放到 ∠ACD上,会出现什么结果呢?
发现:∠ACD=∠ABC+ ∠BAC
归纳总结
∠ACD=∠ABC+ ∠BAC
即:三角形的一个外角等于与它不相邻的两个内角的和.
可知:三角形的一个外角大于任何一个与它不相邻的内角.
因为:∠ACD+∠ACB=180°
∠ABC+ ∠BAC+ ∠ACB=180 °
三角形外角的性质
探究新知
B
C
A
)
)
1
2
3
)
与三角形的每个内角相邻的外角分别有两个, 这两个外角是对顶角, 因此取其一作为三角形的外角.
那么∠1+ ∠2+ ∠3就是△ABC的外角和.
)
做一做
所以:∠1+ ∠2+ ∠3= 360 °
∠1+ = 180 °
∠2+ = 180 °
∠3+ = 180 °
三式相加可以得到
∠1+ ∠2+ ∠3+ + + = .
∠ACB
∠BAC
∠ABC
∠ACB
∠BAC
∠ABC
540 °
而 ∠ACB +∠BAC +∠ABC= 180 °
归纳总结
三角形的外角和等于360°.
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
典例精讲
例:D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°∠BAC=70°
求:
(1)∠B的度数(2)∠C的度数
解:(1)∵∠ADC是△ABD的外角(已知)
∴∠B+∠BAD=∠ADC=80°(三角形的一个外角等于与它不相邻的两个内角之和)
又∵∠B=∠BAD(已知)
∴∠B=80° =40°(等量代换)
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)
∴∠C=180°-∠B-∠BAC(等式的性质)
=180°-40°-70°
=70°
归纳概念
总结: 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
课堂练习
1.将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
C
2.判断∠1与∠3的大小,并说明理由。
∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1
解:∠3 > ∠1
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
(三角形的外角等于与它不相邻的两内角的和)
∴ ∠A+∠B+∠C+∠D+∠E
=(∠A+ ∠D)+(∠B+ ∠E)+∠C
=∠1+∠2+∠C=180°
3.如图所示:求∠A+∠B+∠C+∠D+∠E的度数?
4.如图,D是△ABC中的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
解:设∠1=∠2=x°,∵∠4是△ABD的外角,∴∠4=∠3=∠1+∠2=2x°,
又∵∠BAC+∠3+∠2=180°,∴66°+2x°+x°=180°,∴x°=38°,∴∠DAC=∠BAC-∠1=66°-38°=28°
课堂总结
三角形内角和与外角和
三角形的
内角和
三角形内角和等于180 °
直角三角形的两锐角互余
三角形外角和
定义
角一边必须是三角形的一边,另一边必须是三角形另一边的延长线
性质
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和
三角形的外角和等于360 °
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
