人教版数学八年级下册18.2特殊的平行四边形 巩固练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2特殊的平行四边形 巩固练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 613.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 08:56:24 | ||
图片预览

文档简介
18.2特殊的平行四边形巩固练习
一、单选题
1.如图,在矩形中,两条对角线与相交于点,,则的长为( )
A.4 B.8 C. D.
2.如图,矩形中,、交于点,、分别为、的中点.若,,则的长为( )
A.2 B.4 C.8 D.16
3.如图,在中,、分别为、的中点,点在上,且,若,,则的长为( )
A.1.5 B.1 C.0.5 D.2
4.如图,菱形的对角线交于点O,E为边的中点,若菱形的周长为24,则的长是( )
A.1 B.20 C.3 D.4
5.已知在菱形中,,,则菱形的面积为( )
A.160 B.80 C.40 D.96
6.矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.每条对角线平分一组对角 D.对角线相等
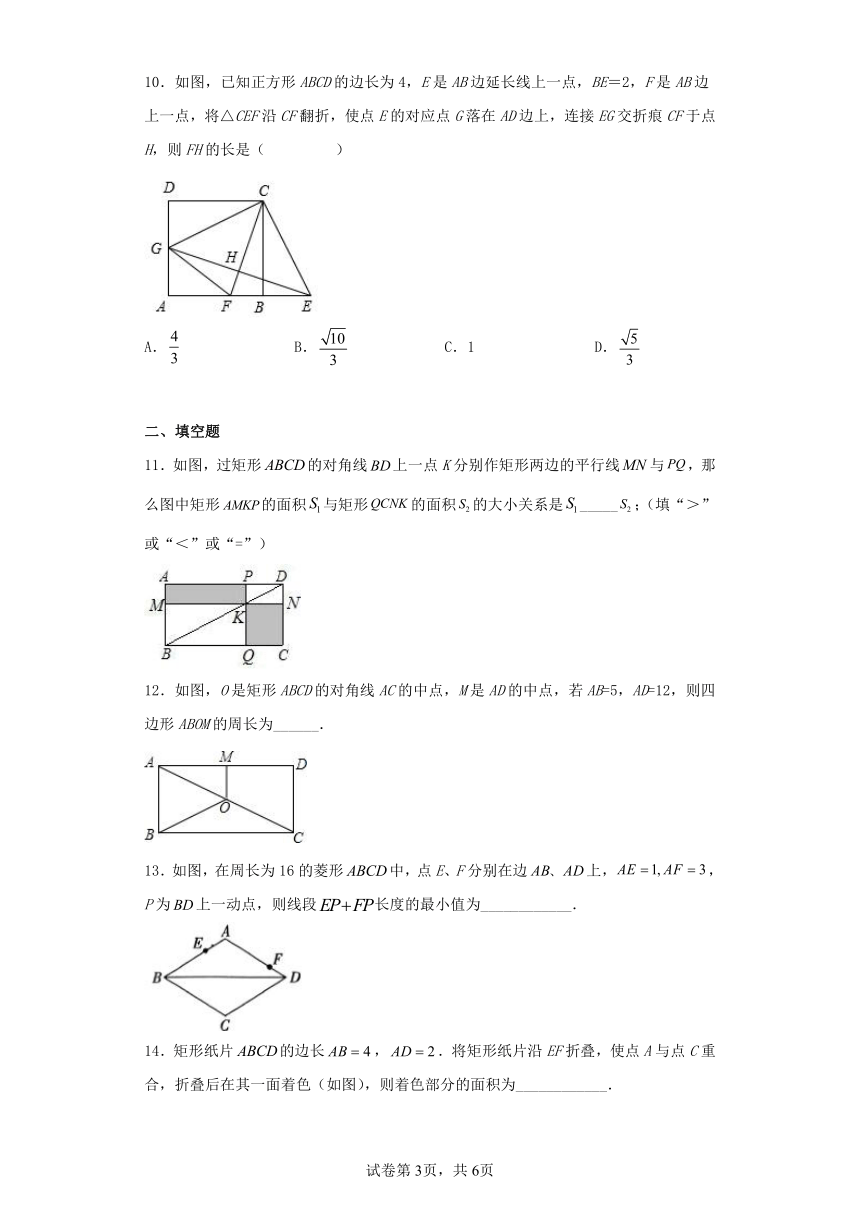
7.如图所示,正方形的面积为12,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A. B. C. D.
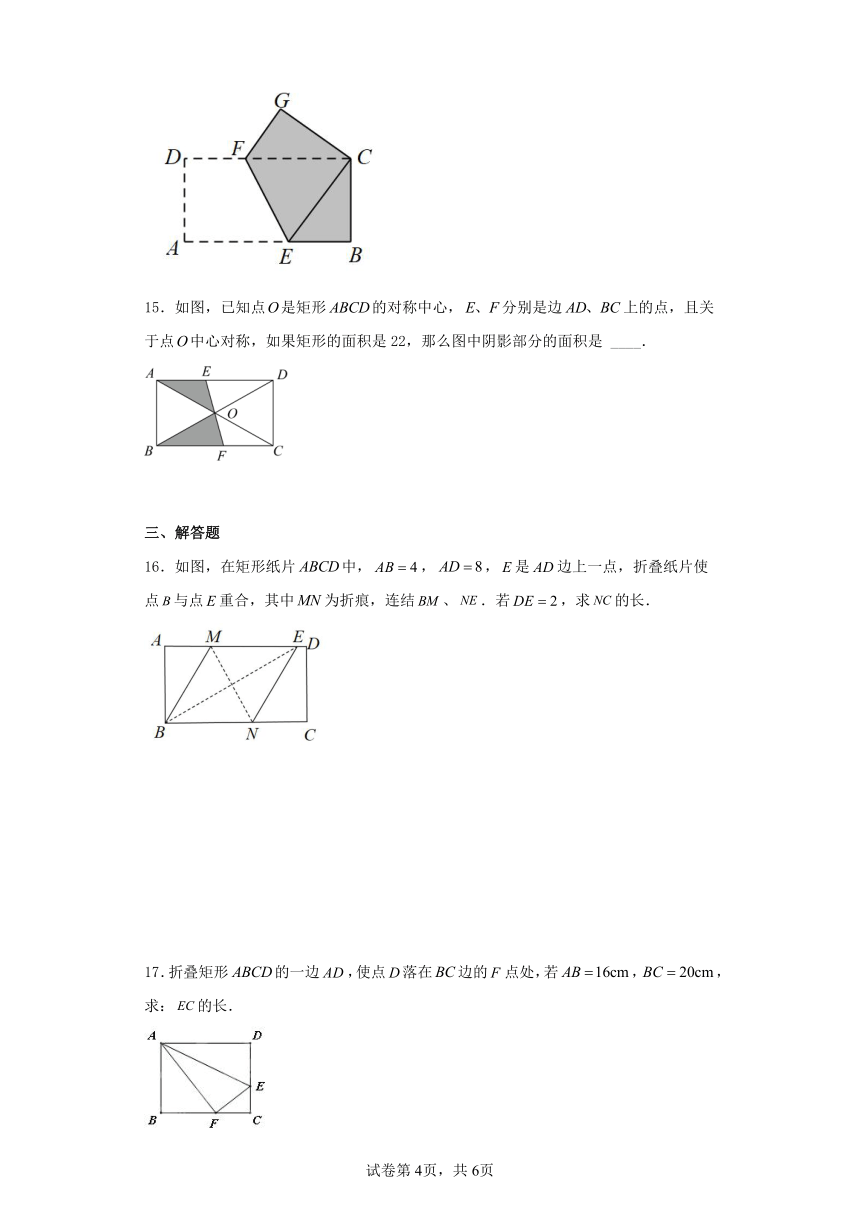
8.一个大矩形按如图方式分割成十二个小矩形,且只有标号为,,,的四个小矩形为正方形,在满足条件的所有分割中,若知道十二个小矩形中个小矩形的周长,就一定能算出这个大矩形的面积,则的最小值是( )
A.2 B.3 C.4 D.5
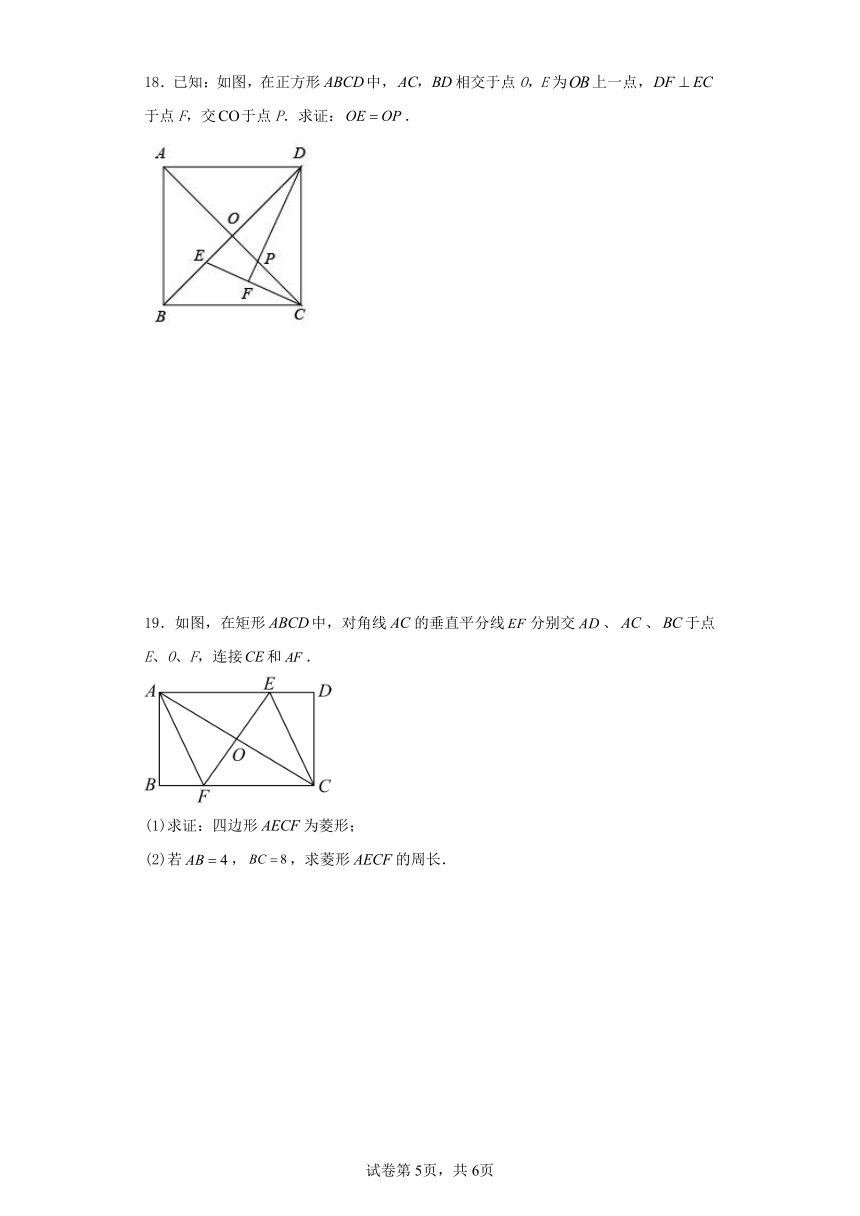
9.如图,正方形和正方形中,点D在上,,H是的中点,那么的长是( )
A.2.5 B. C. D.2
10.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A. B. C.1 D.
二、填空题
11.如图,过矩形的对角线上一点K分别作矩形两边的平行线与,那么图中矩形的面积与矩形的面积的大小关系是_____;(填“>”或“<”或“=”)
12.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为______.
13.如图,在周长为16的菱形中,点E、F分别在边上,,P为上一动点,则线段长度的最小值为____________.
14.矩形纸片的边长,.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为____________.
15.如图,已知点是矩形的对称中心,分别是边上的点,且关于点中心对称,如果矩形的面积是22,那么图中阴影部分的面积是 ____.
三、解答题
16.如图,在矩形纸片中,,,是边上一点,折叠纸片使点与点重合,其中为折痕,连结、.若,求的长.
17.折叠矩形的一边,使点落在边的点处,若,,求:的长.
18.已知:如图,在正方形中,相交于点O,E为上一点,于点F,交于点P.求证:.
19.如图,在矩形中,对角线的垂直平分线分别交、、于点E、O、F,连接和.
(1)求证:四边形为菱形;
(2)若,,求菱形的周长.
20.如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)判断:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的有 ;
(2)如图2,垂美四边形两组对边、与、之间有怎样的数量关系?写出你的猜想,并给出证明;
(3)如图3,分别以的直角边和斜边为边向外作正方形和正方形,连接、、,与交于点O,已知,,求的中线的长.
试卷第6页,共6页
试卷第5页,共6页
参考答案
1.D
2.B
3.A
4.C
5.D
6.D
7.B
8.B
9.B
10.B
11.
12.20
13.
14.
15.
16.解:∵B、E两点关于直线对称,
∴,
在矩形中,,
∴,
∴,
∴,
∴,
∴四边形是菱形;
设菱形的边长为x,
∴,
在中,,
∴,
∴解得:.
∴.
17.解:四边形为矩形,
,,;
折叠矩形的一边,使点落在边的点处,
,
由勾股定理得:,
,
;
设,;
在中,由勾股定理得:,
解得:,
.
18.证明:∵四边形是正方形,
∴,
∴,
∴,
∴,且,,
∴,
∴.
19.(1)证明:是的垂直平分线,
,,
四边形是矩形,
∴,
,
在和中,
,
;
又,
四边形是平行四边形,
又
四边形是菱形;
(2)解:设,
是的垂直平分线,
,
∵,
∴,
∵四边形是矩形,
∴,
∴在中,由勾股定理得:
,
即,
解得:,
,
菱形的周长为.
20.(1)解:∵菱形、正方形的对角线垂直,
∴菱形、正方形都是垂美四边形.
故答案为:菱形和正方形.
(2)解:猜想:.
理由:∵,
∴,
由勾股定理,得,
,
∴.
(3)解:连接、,设,交于点M,如图所示:
∵四边形和为正方形,
∴,,,
∴,
即,
∵在和中,
,
∴,
∴,
∵,
∴,即,
∴四边形是垂美四边形,
∴,
∵,,
∴,, ,
∴,
∴,
∴.
答案第4页,共4页
答案第3页,共4页
一、单选题
1.如图,在矩形中,两条对角线与相交于点,,则的长为( )
A.4 B.8 C. D.
2.如图,矩形中,、交于点,、分别为、的中点.若,,则的长为( )
A.2 B.4 C.8 D.16
3.如图,在中,、分别为、的中点,点在上,且,若,,则的长为( )
A.1.5 B.1 C.0.5 D.2
4.如图,菱形的对角线交于点O,E为边的中点,若菱形的周长为24,则的长是( )
A.1 B.20 C.3 D.4
5.已知在菱形中,,,则菱形的面积为( )
A.160 B.80 C.40 D.96
6.矩形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.每条对角线平分一组对角 D.对角线相等
7.如图所示,正方形的面积为12,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A. B. C. D.
8.一个大矩形按如图方式分割成十二个小矩形,且只有标号为,,,的四个小矩形为正方形,在满足条件的所有分割中,若知道十二个小矩形中个小矩形的周长,就一定能算出这个大矩形的面积,则的最小值是( )
A.2 B.3 C.4 D.5
9.如图,正方形和正方形中,点D在上,,H是的中点,那么的长是( )
A.2.5 B. C. D.2
10.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是( )
A. B. C.1 D.
二、填空题
11.如图,过矩形的对角线上一点K分别作矩形两边的平行线与,那么图中矩形的面积与矩形的面积的大小关系是_____;(填“>”或“<”或“=”)
12.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为______.
13.如图,在周长为16的菱形中,点E、F分别在边上,,P为上一动点,则线段长度的最小值为____________.
14.矩形纸片的边长,.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为____________.
15.如图,已知点是矩形的对称中心,分别是边上的点,且关于点中心对称,如果矩形的面积是22,那么图中阴影部分的面积是 ____.
三、解答题
16.如图,在矩形纸片中,,,是边上一点,折叠纸片使点与点重合,其中为折痕,连结、.若,求的长.
17.折叠矩形的一边,使点落在边的点处,若,,求:的长.
18.已知:如图,在正方形中,相交于点O,E为上一点,于点F,交于点P.求证:.
19.如图,在矩形中,对角线的垂直平分线分别交、、于点E、O、F,连接和.
(1)求证:四边形为菱形;
(2)若,,求菱形的周长.
20.如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)判断:在平行四边形、矩形、菱形、正方形中,一定是垂美四边形的有 ;
(2)如图2,垂美四边形两组对边、与、之间有怎样的数量关系?写出你的猜想,并给出证明;
(3)如图3,分别以的直角边和斜边为边向外作正方形和正方形,连接、、,与交于点O,已知,,求的中线的长.
试卷第6页,共6页
试卷第5页,共6页
参考答案
1.D
2.B
3.A
4.C
5.D
6.D
7.B
8.B
9.B
10.B
11.
12.20
13.
14.
15.
16.解:∵B、E两点关于直线对称,
∴,
在矩形中,,
∴,
∴,
∴,
∴,
∴四边形是菱形;
设菱形的边长为x,
∴,
在中,,
∴,
∴解得:.
∴.
17.解:四边形为矩形,
,,;
折叠矩形的一边,使点落在边的点处,
,
由勾股定理得:,
,
;
设,;
在中,由勾股定理得:,
解得:,
.
18.证明:∵四边形是正方形,
∴,
∴,
∴,
∴,且,,
∴,
∴.
19.(1)证明:是的垂直平分线,
,,
四边形是矩形,
∴,
,
在和中,
,
;
又,
四边形是平行四边形,
又
四边形是菱形;
(2)解:设,
是的垂直平分线,
,
∵,
∴,
∵四边形是矩形,
∴,
∴在中,由勾股定理得:
,
即,
解得:,
,
菱形的周长为.
20.(1)解:∵菱形、正方形的对角线垂直,
∴菱形、正方形都是垂美四边形.
故答案为:菱形和正方形.
(2)解:猜想:.
理由:∵,
∴,
由勾股定理,得,
,
∴.
(3)解:连接、,设,交于点M,如图所示:
∵四边形和为正方形,
∴,,,
∴,
即,
∵在和中,
,
∴,
∴,
∵,
∴,即,
∴四边形是垂美四边形,
∴,
∵,,
∴,, ,
∴,
∴,
∴.
答案第4页,共4页
答案第3页,共4页
