3.2.1函数的单调性 课件(共25张PPT)
文档属性
| 名称 | 3.2.1函数的单调性 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 11:32:52 | ||
图片预览







文档简介
(共25张PPT)
3.2 函数的基本性质
3.2.1 函数的单调性
(第一课时)
前面我们学习了函数的定义和表示法, 知道函数是描述客观世界中变量之间的一种对应关系,这样 我们就可以通过研究函数性质来把握客观世界中事物的变化规律。
那么什么是函数的性质呢?
新课引入
总体而言,函数性质就是变化中的不变性,变化中的规律性。
研究函数性质就是学会在运动变化中发现规律。
请同学们回想一下初中我们学习过哪些函数?
我们是通过什么来研究它们的性质的呢?
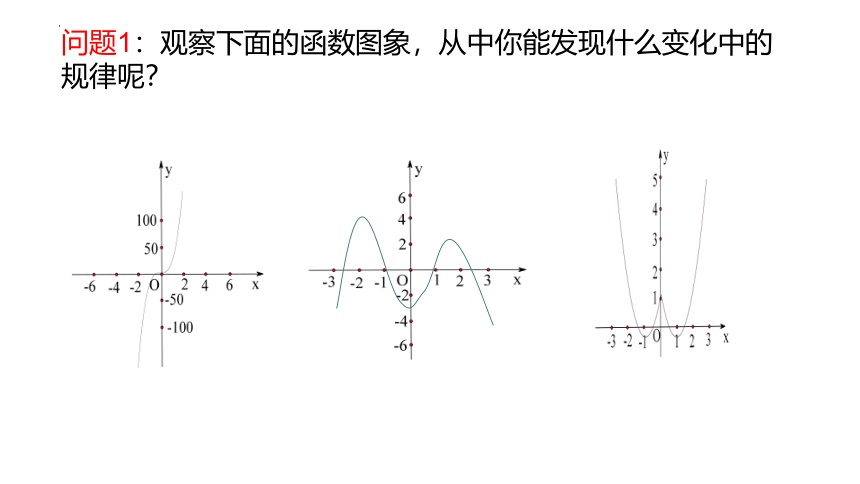
问题1:观察下面的函数图象,从中你能发现什么变化中的规律呢?
函数的单调性
本节课我们主要是用符号语言定量地刻画函数值随自变量的增大而增大或减小的性质
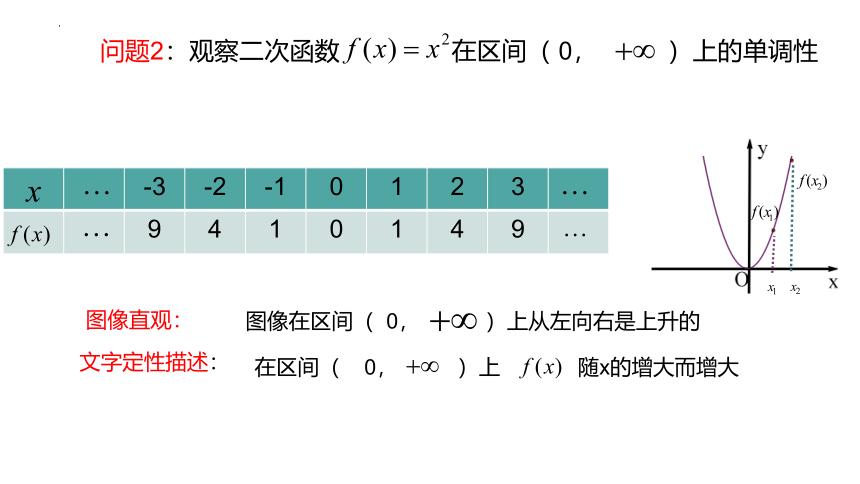
问题2:观察二次函数 在区间( 0, )上的单调性
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
图像在区间( 0, )上从左向右是上升的
在区间( 0, )上 随x的增大而增大
文字定性描述:
图像直观:
如何用符号语言定量刻画二次函数 在区间( 0, )上的单调性?
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
当x1这里x1,x2有多少对?只取(0, )上的某些数对是否可以?应该如何表述更严密呢?
x1、x2∈(0, ),当x1对于函数 你能模仿上述方法给出在区间( ,0)上的单调性吗?
x1、x2∈( , 0),当x1f(x2)
仿照函数 的单调性的描述方法,请你用严格的符号语言来刻画函数 的单调性
问题3:归纳以上两个函数单调性的刻画方法,给出函数 在区间Ⅰ上单调性的定义。
特别地,当函数 在它的定义域上单调递增时,我们就称它是增函数.
当函数 在它的定义域上单调递减时,我们就称它是减函数.
如果y=f(x)在区间I上是单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫做y=f(x)的单调区间.
判断正误:
(1)所有函数在定义域上都具有单调性. ( )
(2)定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;
( )
(3)若f(x)是R上的减函数,则f(-3)>f(2). ( )
(4)若函数f(x)在区间(1,2]和(2,3)上均单调递增,则函数f(x)在区间(1,3)上也单调递增. ( )
y
x
O
1
2
f(1)
f(2)
练习.定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,y=f(x)是单调递增还是单调递减.
解:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5];
在区间[-5,-2),[1,3)上是单调递减,在区间[-2,1),[3,5]上是单调递增.
注意:单调区间之间不可以 用“ ”连接.
例1:根据定义,研究函数 的单调性.
分析:根据函数单调性的定义,需要考察当 时, 还是 .根据实数大小关系的基本事实,只需要考察 与0的大小关系.
函数单调性定义的应用
定义法证明或讨论函数单调性的步骤
(1)取值:在该区间内任取x1、x2,且x1(2)作差变形:作差f(x1)-f(x2),并通过因式分解、通分、配方、有理化等手段,转化为易判断正负的式子;
(3)定号:将变形结果与0作比较,确定f(x1)-f(x2)的符号;
(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性.
例2:
物理学中的玻意耳定律 (为正常数)告诉我们,对于一定量的气体,当其体积V减少时,压强P将增大.试用函数的单调性证明.
【分析】根据题意,只要证明函数 是减函数即可.
例2是一个物理学中的公式,我们可以体会到函数模型可以用来刻画现实世界中的现象,数学的研究是将一类运动变化的现象抽象成一类函数,通过研究这一类函数的性质而获得事物的变化规律。
例2:物理学中的玻意耳定律 (为正常数)告诉我们,对于一定量的气体,当其体积V减少时,压强P将增大.试用函数的单调性证明.
请你以例2为母题从中抽象出一些新的函数模型并说出这些函数模型的单调性。
合作交流
1.函数单调性的定义;
课堂小结
这节课我们学习了哪些内容?
2.函数单调性的判断:(1)定义法;(2)图象法;
3.用定义证明单调性的步骤:
(1)取值;(2)作差变形;(3)定号;(4)结论.
你对函数性质的研究过程有什么体会?
图像直观
定性描述
定量刻画
作业:课本第79页 练习. 第1、2、3题
数学是打开科学大门的钥匙,
数学是人类思考中最高的成就。
Thank you for watching !
3.2 函数的基本性质
3.2.1 函数的单调性
(第一课时)
前面我们学习了函数的定义和表示法, 知道函数是描述客观世界中变量之间的一种对应关系,这样 我们就可以通过研究函数性质来把握客观世界中事物的变化规律。
那么什么是函数的性质呢?
新课引入
总体而言,函数性质就是变化中的不变性,变化中的规律性。
研究函数性质就是学会在运动变化中发现规律。
请同学们回想一下初中我们学习过哪些函数?
我们是通过什么来研究它们的性质的呢?
问题1:观察下面的函数图象,从中你能发现什么变化中的规律呢?
函数的单调性
本节课我们主要是用符号语言定量地刻画函数值随自变量的增大而增大或减小的性质
问题2:观察二次函数 在区间( 0, )上的单调性
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
图像在区间( 0, )上从左向右是上升的
在区间( 0, )上 随x的增大而增大
文字定性描述:
图像直观:
如何用符号语言定量刻画二次函数 在区间( 0, )上的单调性?
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
当x1
x1、x2∈(0, ),当x1
x1、x2∈( , 0),当x1
仿照函数 的单调性的描述方法,请你用严格的符号语言来刻画函数 的单调性
问题3:归纳以上两个函数单调性的刻画方法,给出函数 在区间Ⅰ上单调性的定义。
特别地,当函数 在它的定义域上单调递增时,我们就称它是增函数.
当函数 在它的定义域上单调递减时,我们就称它是减函数.
如果y=f(x)在区间I上是单调递增或单调递减,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫做y=f(x)的单调区间.
判断正误:
(1)所有函数在定义域上都具有单调性. ( )
(2)定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;
( )
(3)若f(x)是R上的减函数,则f(-3)>f(2). ( )
(4)若函数f(x)在区间(1,2]和(2,3)上均单调递增,则函数f(x)在区间(1,3)上也单调递增. ( )
y
x
O
1
2
f(1)
f(2)
练习.定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上,y=f(x)是单调递增还是单调递减.
解:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5];
在区间[-5,-2),[1,3)上是单调递减,在区间[-2,1),[3,5]上是单调递增.
注意:单调区间之间不可以 用“ ”连接.
例1:根据定义,研究函数 的单调性.
分析:根据函数单调性的定义,需要考察当 时, 还是 .根据实数大小关系的基本事实,只需要考察 与0的大小关系.
函数单调性定义的应用
定义法证明或讨论函数单调性的步骤
(1)取值:在该区间内任取x1、x2,且x1
(3)定号:将变形结果与0作比较,确定f(x1)-f(x2)的符号;
(4)结论:根据f(x1)-f(x2)的符号及定义判断单调性.
例2:
物理学中的玻意耳定律 (为正常数)告诉我们,对于一定量的气体,当其体积V减少时,压强P将增大.试用函数的单调性证明.
【分析】根据题意,只要证明函数 是减函数即可.
例2是一个物理学中的公式,我们可以体会到函数模型可以用来刻画现实世界中的现象,数学的研究是将一类运动变化的现象抽象成一类函数,通过研究这一类函数的性质而获得事物的变化规律。
例2:物理学中的玻意耳定律 (为正常数)告诉我们,对于一定量的气体,当其体积V减少时,压强P将增大.试用函数的单调性证明.
请你以例2为母题从中抽象出一些新的函数模型并说出这些函数模型的单调性。
合作交流
1.函数单调性的定义;
课堂小结
这节课我们学习了哪些内容?
2.函数单调性的判断:(1)定义法;(2)图象法;
3.用定义证明单调性的步骤:
(1)取值;(2)作差变形;(3)定号;(4)结论.
你对函数性质的研究过程有什么体会?
图像直观
定性描述
定量刻画
作业:课本第79页 练习. 第1、2、3题
数学是打开科学大门的钥匙,
数学是人类思考中最高的成就。
Thank you for watching !
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
