吉林省长春市朝阳区2022-2023学年九年级下学期3月月考数学试题(无答案)
文档属性
| 名称 | 吉林省长春市朝阳区2022-2023学年九年级下学期3月月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 15:44:24 | ||
图片预览


文档简介
九年级数学测试
一、选择题(本大题共8小题,每小题3分,共24分)
1.如图所示的几何体的左视图是( )
A. B. C. D.
2.已知a>b,则下列各式中一定成立的是( )
A.a-b<0 B.2a-1<2b-1 C. D.
3.下列二次根式是最简二次根式的是( )
A. B. C. D.
4.若关于x的方程有实数根,则实数m的取值范围是( )
A. B. C. D.
5.如图,某大桥主塔的正面示意图是一个轴对称图形,小明测得桥面宽度AB=a米,∠OAB=70°,则点O到桥面的距离(单位:米)是( )
A. B. C. D.
6.如图在中,半径OA垂直于弦BC,点D在圆上且∠ADC=30°,则∠AOB度数是( )
A.15° B.30° C.45° D.60°
7.如图,中,由∠ACB=90°,用圆规和直尺作图,分成两个三角形,其中一定至少有一个三角形是等腰三角形,其作法错误的是( )
A. B. C. D.
8.如图,点E为对角线的交点,点B在y轴正半轴上,CD在x轴上,点M为AB的中点.双曲线过点E,M,连接EM.已知,则k的值是( )
A.-8 B.-6 C.-4 D.-2
二、填空题(本大题共6小题,每小题3分,共18分)
9.直接写出计算结果:_________.
10.当x=_________时,分式的值为零.
11.在我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:由大小两种盛酒的桶,已知五个大桶和一个小桶共可盛酒3斛(斛:一种容量单位),一个大桶和五个小桶共可盛酒2斛,设一个小桶和一个大桶分别可盛酒x斛和y斛,根据题意可列方程组为_________.
12.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,则贴纸部分面积是_________.(结果保留)
13.中国结象征着中华民族的历史文化与精神,小贤家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形,测得BD=24cm,AC=32cm,直线EF⊥AB交两对边于点E,F,则EF的长为_________cm.
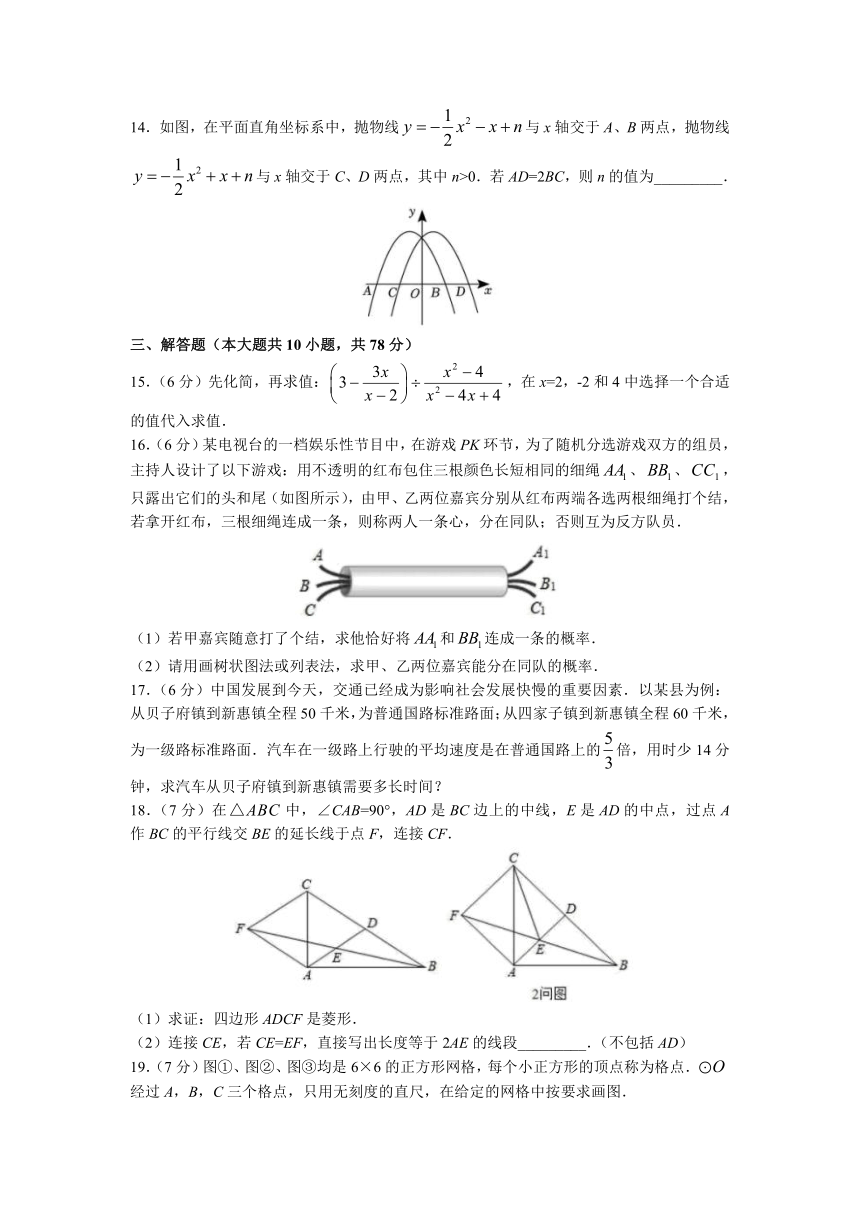
14.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点,抛物线与x轴交于C、D两点,其中n>0.若AD=2BC,则n的值为_________.
三、解答题(本大题共10小题,共78分)
15.(6分)先化简,再求值:,在x=2,-2和4中选择一个合适的值代入求值.
16.(6分)某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的红布包住三根颜色长短相同的细绳、、,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从红布两端各选两根细绳打个结,若拿开红布,三根细绳连成一条,则称两人一条心,分在同队;否则互为反方队员.
(1)若甲嘉宾随意打了个结,求他恰好将和连成一条的概率.
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分在同队的概率.
17.(6分)中国发展到今天,交通已经成为影响社会发展快慢的重要因素.以某县为例:从贝子府镇到新惠镇全程50千米,为普通国路标准路面;从四家子镇到新惠镇全程60千米,为一级路标准路面.汽车在一级路上行驶的平均速度是在普通国路上的倍,用时少14分钟,求汽车从贝子府镇到新惠镇需要多长时间?
18.(7分)在中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)连接CE,若CE=EF,直接写出长度等于2AE的线段_________.(不包括AD)
19.(7分)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点.经过A,B,C三个格点,只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中的圆上找一点D,使得∠ADC=∠ABC.
(2)在图②中的圆上找一点E,使得OE平分AC.
(3)在图③中的圆上找一点F,使得CF平分∠ACB.
20.(7分)为响应“双减”政策,落实好作业减负,某校对本校学生每天完成作业所用时间的情况进行了抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并根据统计结果制成了条形统计图和扇形统计图,请结合图中信息回答下列问题:
(1)本次调查的学生人数为_________;
(2)补全条形统计图;
(3)根据图中提供的信息,可知下列结论正确的是_________(填正确结论的序号);
①由图1知,学生完成作业所用时间的中位数在90~120分钟内
②由图1知,学生完成作业所用时间的众数60~90分钟内
③图2中,90~120时间段对应的扇形圆心角为108°
(4)学生每天完成作业的时间不超过120分钟,视为课业负担适中,根据以上调查,估计该校九年级560名学生中,课业负担适中的学生有多少人?
21.(8分)用充电器给某手机充电时,其屏幕的起始画面如图①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量y(单位:%)与充电时间x(单位:h)的函数图象分别为图②中的线段AB、AC.
根据以上信息,回答下列问题:
(1)在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用_________小时.
(2)求线段AB对应的函数表达式,并写出其自变量的取值范围;
(3)在目前电量20%得情况下,已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电-耗电-充电”的时间恰好是6h,直接写出a的值.
22.(9分)问题呈现:
(1)如图①,在一次数学折纸活动中,有一张矩形纸片,点E在AD上,点F在BC上,小华同学将这张矩形纸片沿EF翻折得到四边形,交AD于点H,小华认为是等腰三角形,你认为小华的判断正确吗?请说明理由:
问题拓展:
(2)如图②,在(1)的条件下,当点C的对应点落在AD上时,已知DE=a,CD=b,CF=c,写出a、b、c满足的数量关系,并证明你的结论;
问题应用:
(3)如图③,在平行四边形中,AB=3,AD=4.将平行四边形沿对角线AC翻折得到,点D、C、E在一条直线上,直接写出平行四边形的面积.
23.(10分)在中,AB=AC=10,的面积为30,点D为AC的中点,动点P由点A以每秒5个单位的速度向点B运动,连结PD,以PD、DC为邻边作,设与的重叠部分面积为S,设点P的运动时间为.
(1)_________
(2)求点Q落在BC上时t的值.
(3)在点P运动的过程中,求S与t之间的函数关系式.
(4)若点A关于PD所在直线的对称点为,当点落在一边上的高上时,直接写出t的值.
24.(12分)已知抛物线(b、c是常数)的顶点B坐标为,抛物线的对称轴为直线l,点A为抛物线与x轴的右交点,作直线AB.点P是抛物线上的任意一点,其横坐标为m,过点P作x轴的垂线交直线AB于点Q,过点P作PN⊥l于点N,以PQ、PN为边作矩形PQMN.
(1)b=_________,c=_________.
(2)当点Q在线段AB上(点Q不与A、B重合)时,求PQ的长度d与m的函数关系式,并直接写出d的最大值.
(3)当抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P的坐标.
(4)矩形PQMN的任意两个顶点到直线AB的距离相等时,直接写出m的值.
一、选择题(本大题共8小题,每小题3分,共24分)
1.如图所示的几何体的左视图是( )
A. B. C. D.
2.已知a>b,则下列各式中一定成立的是( )
A.a-b<0 B.2a-1<2b-1 C. D.
3.下列二次根式是最简二次根式的是( )
A. B. C. D.
4.若关于x的方程有实数根,则实数m的取值范围是( )
A. B. C. D.
5.如图,某大桥主塔的正面示意图是一个轴对称图形,小明测得桥面宽度AB=a米,∠OAB=70°,则点O到桥面的距离(单位:米)是( )
A. B. C. D.
6.如图在中,半径OA垂直于弦BC,点D在圆上且∠ADC=30°,则∠AOB度数是( )
A.15° B.30° C.45° D.60°
7.如图,中,由∠ACB=90°,用圆规和直尺作图,分成两个三角形,其中一定至少有一个三角形是等腰三角形,其作法错误的是( )
A. B. C. D.
8.如图,点E为对角线的交点,点B在y轴正半轴上,CD在x轴上,点M为AB的中点.双曲线过点E,M,连接EM.已知,则k的值是( )
A.-8 B.-6 C.-4 D.-2
二、填空题(本大题共6小题,每小题3分,共18分)
9.直接写出计算结果:_________.
10.当x=_________时,分式的值为零.
11.在我国古代数学著作《九章算术》中记载:“今有大器五小器一容三斛,大器一小器五容二斛.问大小器各容几何.”其大意为:由大小两种盛酒的桶,已知五个大桶和一个小桶共可盛酒3斛(斛:一种容量单位),一个大桶和五个小桶共可盛酒2斛,设一个小桶和一个大桶分别可盛酒x斛和y斛,根据题意可列方程组为_________.
12.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,则贴纸部分面积是_________.(结果保留)
13.中国结象征着中华民族的历史文化与精神,小贤家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形,测得BD=24cm,AC=32cm,直线EF⊥AB交两对边于点E,F,则EF的长为_________cm.
14.如图,在平面直角坐标系中,抛物线与x轴交于A、B两点,抛物线与x轴交于C、D两点,其中n>0.若AD=2BC,则n的值为_________.
三、解答题(本大题共10小题,共78分)
15.(6分)先化简,再求值:,在x=2,-2和4中选择一个合适的值代入求值.
16.(6分)某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的红布包住三根颜色长短相同的细绳、、,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从红布两端各选两根细绳打个结,若拿开红布,三根细绳连成一条,则称两人一条心,分在同队;否则互为反方队员.
(1)若甲嘉宾随意打了个结,求他恰好将和连成一条的概率.
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分在同队的概率.
17.(6分)中国发展到今天,交通已经成为影响社会发展快慢的重要因素.以某县为例:从贝子府镇到新惠镇全程50千米,为普通国路标准路面;从四家子镇到新惠镇全程60千米,为一级路标准路面.汽车在一级路上行驶的平均速度是在普通国路上的倍,用时少14分钟,求汽车从贝子府镇到新惠镇需要多长时间?
18.(7分)在中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形.
(2)连接CE,若CE=EF,直接写出长度等于2AE的线段_________.(不包括AD)
19.(7分)图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点.经过A,B,C三个格点,只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图①中的圆上找一点D,使得∠ADC=∠ABC.
(2)在图②中的圆上找一点E,使得OE平分AC.
(3)在图③中的圆上找一点F,使得CF平分∠ACB.
20.(7分)为响应“双减”政策,落实好作业减负,某校对本校学生每天完成作业所用时间的情况进行了抽样调查,随机调查了九年级部分学生每天完成作业所用的时间,并根据统计结果制成了条形统计图和扇形统计图,请结合图中信息回答下列问题:
(1)本次调查的学生人数为_________;
(2)补全条形统计图;
(3)根据图中提供的信息,可知下列结论正确的是_________(填正确结论的序号);
①由图1知,学生完成作业所用时间的中位数在90~120分钟内
②由图1知,学生完成作业所用时间的众数60~90分钟内
③图2中,90~120时间段对应的扇形圆心角为108°
(4)学生每天完成作业的时间不超过120分钟,视为课业负担适中,根据以上调查,估计该校九年级560名学生中,课业负担适中的学生有多少人?
21.(8分)用充电器给某手机充电时,其屏幕的起始画面如图①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量y(单位:%)与充电时间x(单位:h)的函数图象分别为图②中的线段AB、AC.
根据以上信息,回答下列问题:
(1)在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用_________小时.
(2)求线段AB对应的函数表达式,并写出其自变量的取值范围;
(3)在目前电量20%得情况下,已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电-耗电-充电”的时间恰好是6h,直接写出a的值.
22.(9分)问题呈现:
(1)如图①,在一次数学折纸活动中,有一张矩形纸片,点E在AD上,点F在BC上,小华同学将这张矩形纸片沿EF翻折得到四边形,交AD于点H,小华认为是等腰三角形,你认为小华的判断正确吗?请说明理由:
问题拓展:
(2)如图②,在(1)的条件下,当点C的对应点落在AD上时,已知DE=a,CD=b,CF=c,写出a、b、c满足的数量关系,并证明你的结论;
问题应用:
(3)如图③,在平行四边形中,AB=3,AD=4.将平行四边形沿对角线AC翻折得到,点D、C、E在一条直线上,直接写出平行四边形的面积.
23.(10分)在中,AB=AC=10,的面积为30,点D为AC的中点,动点P由点A以每秒5个单位的速度向点B运动,连结PD,以PD、DC为邻边作,设与的重叠部分面积为S,设点P的运动时间为.
(1)_________
(2)求点Q落在BC上时t的值.
(3)在点P运动的过程中,求S与t之间的函数关系式.
(4)若点A关于PD所在直线的对称点为,当点落在一边上的高上时,直接写出t的值.
24.(12分)已知抛物线(b、c是常数)的顶点B坐标为,抛物线的对称轴为直线l,点A为抛物线与x轴的右交点,作直线AB.点P是抛物线上的任意一点,其横坐标为m,过点P作x轴的垂线交直线AB于点Q,过点P作PN⊥l于点N,以PQ、PN为边作矩形PQMN.
(1)b=_________,c=_________.
(2)当点Q在线段AB上(点Q不与A、B重合)时,求PQ的长度d与m的函数关系式,并直接写出d的最大值.
(3)当抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P的坐标.
(4)矩形PQMN的任意两个顶点到直线AB的距离相等时,直接写出m的值.
同课章节目录
