吉林省长春市朝阳区2022-2023学年九年级下学期3月月考数学试题(无答案)
文档属性
| 名称 | 吉林省长春市朝阳区2022-2023学年九年级下学期3月月考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 414.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 17:38:16 | ||
图片预览

文档简介
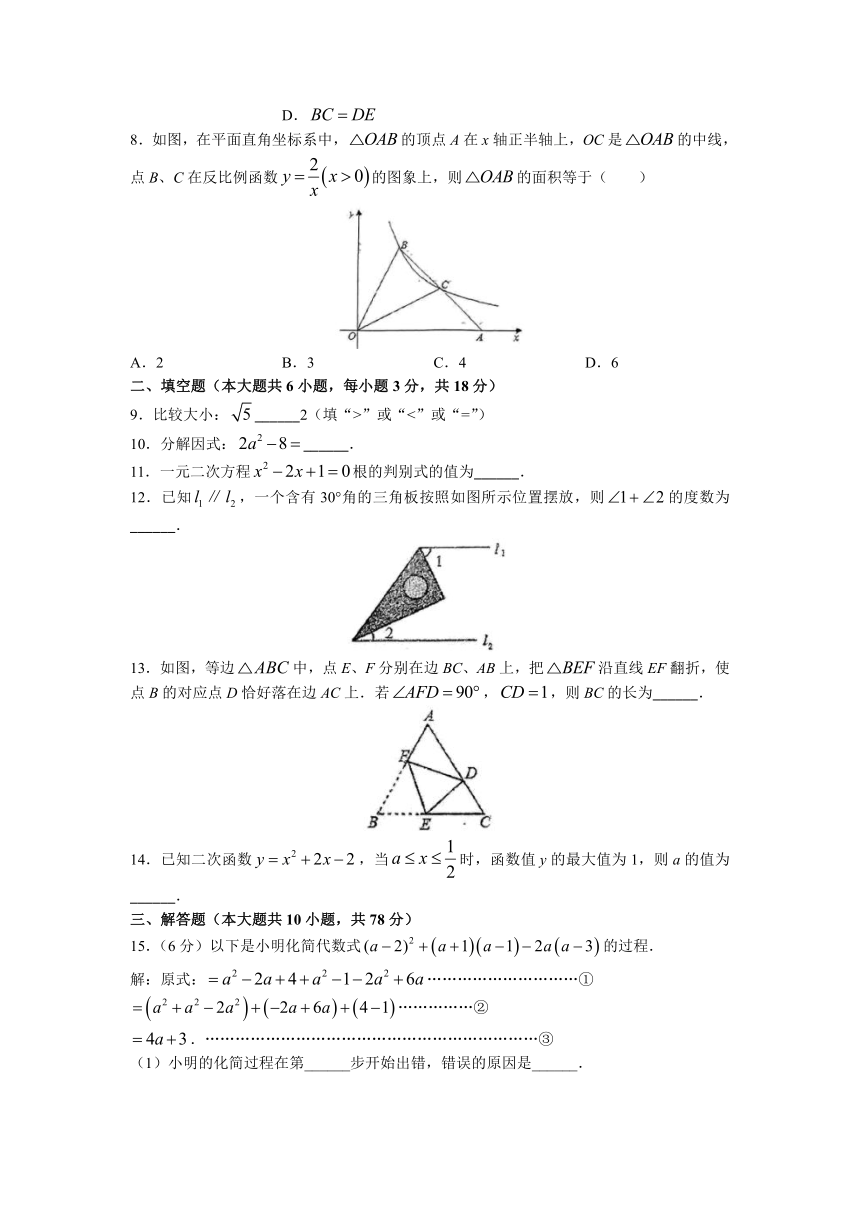
2022-2023学年第二学期九年级阶段性检测数学试题
一、选择题(本大题共8小题,每小题3分,共24分)
1.在数轴上表示下列四个数中,在0和-1之间的数是( )
A. B. C. D.
2.预计到2025年,中国5G用户将超过460000000,将460000000用科学记数法表示为( )
A. B. C. D.
3.如图是某个几何体的三视图,该几何体是( )
A.圆锥 B.圆柱 C.三棱柱 D.六棱柱
4.下列计算正确的是( )
A. B. C. D.
5.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.如图,沿AC的方向开山修路,为了加快速度,要在小山的另一边同时施工,从AC上取一点B,取,已知米,,点A,C,E在同一直线上,那么开挖点E离点D的距离是( )
A.米 B.米 C.米 D.米
7.已知,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A. B. C. D.
8.如图,在平面直角坐标系中,的顶点A在x轴正半轴上,OC是的中线,点B、C在反比例函数的图象上,则的面积等于( )
A.2 B.3 C.4 D.6
二、填空题(本大题共6小题,每小题3分,共18分)
9.比较大小:______2(填“>”或“<”或“=”)
10.分解因式:______.
11.一元二次方程根的判别式的值为______.
12.已知,一个含有30°角的三角板按照如图所示位置摆放,则的度数为______.
13.如图,等边中,点E、F分别在边BC、AB上,把沿直线EF翻折,使点B的对应点D恰好落在边AC上.若,,则BC的长为______.
14.已知二次函数,当时,函数值y的最大值为1,则a的值为______.
三、解答题(本大题共10小题,共78分)
15.(6分)以下是小明化简代数式的过程.
解:原式:…………………………①
……………②
.…………………………………………………………③
(1)小明的化简过程在第______步开始出错,错误的原因是______.
(2)请你帮助小明写出正确的化简过程,并计算当时代数式的值.
16.(6分)甲、乙两个不透明的袋子中分别装有三个标有数字的小球,小球除数字不同外,其余均相同,甲袋中三个小球上分别标有数字1、2、7,乙袋中三个小球上分别标有数字4、5、6,小明分别从甲、乙口袋中通随机摸出一个小球,用画树状图(或列表)的方法,`求小明摸出两个小球上的数字之和为4的倍数的概率.
17.(6分)为迎接五·一国际劳动节,某商店准备采购一批服装,经调查,用1000元采购A种服装的件数与用800元采购B种服装的件数相等,A种服装每件的进价比B种服装多10元,求B种服装每件的进价.
18.(6分)如图、BC为直径,点A是上任意一点(不与点B、C重合),以BC、AB为邻边的平行四边形ABCD的顶点D在外.
(1)当AD与相切时,求的大小.
(2)若的半径为2,,直接写出AC的长.
19.(7分)如图,在的格点图中,为格点三角形,即顶点A、B、C均在格点上,利用无刻度直尺按要求完成下列各题,并保留作图痕迹;
(1)请在图①中AB边上找一点M,使;
(2)请在图②中内部(不含边界)找一点N,使.
20.(8分)东城区为了解各学校中学生在疫情期间体育锻炼的情况,对甲、乙两个学校各180名学生进行了体育测试,从中各随机抽取30名学生的成绩(百分制),并对成绩(单位:分)进行整理、描述和分析.给出了部分成绩信息.
甲校参与测试的学生成绩分布如表:
成绩(分)
甲校 2 3 5 10 10
甲校参与测试的学生成绩在这一组的数据是:
96,96.5,97,97.5,96.5,96.5,97.5,96,96.5,96.5
甲、乙两校参与测试的学生成绩的平均数、中位数、众数如表,根据以上信息,回答下列问题:
学校 平均数 中位数 众数
甲校 96.35 m 99
乙校 95.85 97.5 99
(1)______;
(2)在此次随机抽样测试中,甲校的王同学和乙校的李同学成绩均为97分,则在各自学校参与测试同学中成绩的名次相比较更靠前的是______(填“王”或“李”)同学,请简要说出理由;
(3)在此次随机测试中,乙校大于96分的总人数比甲校大于96分的总人数的2倍少100人,试估计乙校大于96分的总人数.
21.(8分)如图(1),和是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道上从处出发,到达后,以同样的速度返回处,然后重复上述过程;乙在赛道上以1.5 m/s的速度从处出发,到达后以相同的速度回到处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设到池边的距离为y(m),如图2表示甲到池边的距离y(m)与t(s)的函数图象.
(1)赛道的长度是______m,甲的速度是______m/s;
(2)当时,求甲到池边的距离y(m)与t(s)的函数关系式.
(3)第三次相遇时,两人距池边多少米.
22.(9分)【探究】在一次数学课上,老师出示了这样一道题目:“如图,在矩形ABCD中,AC为对角线,,E、F分别为边BC、AD上的点,连结AE、CF,分别将和沿AE、CF翻折,使点B、D的对称点G、H都落在AC上.求证:四边形AECF是平行四边形.”以下是两名学生的解题方法:
甲学生的方法是:首先由矩形的性质和轴对称的性质证得,,,,易得,可得(ASA),由平行四边形的判定定理可得结论.乙学生的方法是:不利用三角形全等知识,依据平行四边形的定义证明.
(1)甲学生证明四边形AECF是平行四边形所用的判定定理的内容是_______________________.
(2)用乙学生的方法完成证明过程.
【应用】当学生们完成证明后,老师又提出了一个问题:
若四边形AECF是菱形,则的值为______.
23.(10分)如图,在中,,,,点P从A出发,沿AC方向以每秒1个单位长度的速度向终点C运动.当点P不与点A、C重合时,将线段AP绕点P逆时针旋转90°,得到线段PQ,以PC、PQ为边作矩形PQHC、点H恰好落在直线BC上.设矩形PQHC与重叠部分的图形面积为S(平方单位),点P的运动时间为t(秒).
(1)证明矩形PQHC的周长是一个定值.
(2)当矩形PQHC为正方形时,求t的值.
(3)在整个运动过程中,存在全等三角形时,求S的值.
(4)矩形PQHC的对角线PH和CQ的交点为M,作点Q关于直线AB的对称点N,当MN与的边平行或者垂直时,直接写出此时的t值.
24.(12分)在平面直角坐标系xOy中,抛物线(b、c为常数)经过点和点,点M在此抛物线上,点M的横坐标为m,点M不与A、B重合.
(1)求此抛物线所对应的函数表达式.
(2)当,求点M的坐标.
(3)作点A关于抛物线对称轴的对称点为点C,当点M到直线AC的距离是点M到x轴距离2倍时,求m的值.
(4)设点E的坐标为,点F的坐标为,连结EF.当抛物线在B、M两点之间的部分(包含B、M两点)与线段EF有1个公共点时,直接写出m的取值范围.
一、选择题(本大题共8小题,每小题3分,共24分)
1.在数轴上表示下列四个数中,在0和-1之间的数是( )
A. B. C. D.
2.预计到2025年,中国5G用户将超过460000000,将460000000用科学记数法表示为( )
A. B. C. D.
3.如图是某个几何体的三视图,该几何体是( )
A.圆锥 B.圆柱 C.三棱柱 D.六棱柱
4.下列计算正确的是( )
A. B. C. D.
5.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.如图,沿AC的方向开山修路,为了加快速度,要在小山的另一边同时施工,从AC上取一点B,取,已知米,,点A,C,E在同一直线上,那么开挖点E离点D的距离是( )
A.米 B.米 C.米 D.米
7.已知,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A. B. C. D.
8.如图,在平面直角坐标系中,的顶点A在x轴正半轴上,OC是的中线,点B、C在反比例函数的图象上,则的面积等于( )
A.2 B.3 C.4 D.6
二、填空题(本大题共6小题,每小题3分,共18分)
9.比较大小:______2(填“>”或“<”或“=”)
10.分解因式:______.
11.一元二次方程根的判别式的值为______.
12.已知,一个含有30°角的三角板按照如图所示位置摆放,则的度数为______.
13.如图,等边中,点E、F分别在边BC、AB上,把沿直线EF翻折,使点B的对应点D恰好落在边AC上.若,,则BC的长为______.
14.已知二次函数,当时,函数值y的最大值为1,则a的值为______.
三、解答题(本大题共10小题,共78分)
15.(6分)以下是小明化简代数式的过程.
解:原式:…………………………①
……………②
.…………………………………………………………③
(1)小明的化简过程在第______步开始出错,错误的原因是______.
(2)请你帮助小明写出正确的化简过程,并计算当时代数式的值.
16.(6分)甲、乙两个不透明的袋子中分别装有三个标有数字的小球,小球除数字不同外,其余均相同,甲袋中三个小球上分别标有数字1、2、7,乙袋中三个小球上分别标有数字4、5、6,小明分别从甲、乙口袋中通随机摸出一个小球,用画树状图(或列表)的方法,`求小明摸出两个小球上的数字之和为4的倍数的概率.
17.(6分)为迎接五·一国际劳动节,某商店准备采购一批服装,经调查,用1000元采购A种服装的件数与用800元采购B种服装的件数相等,A种服装每件的进价比B种服装多10元,求B种服装每件的进价.
18.(6分)如图、BC为直径,点A是上任意一点(不与点B、C重合),以BC、AB为邻边的平行四边形ABCD的顶点D在外.
(1)当AD与相切时,求的大小.
(2)若的半径为2,,直接写出AC的长.
19.(7分)如图,在的格点图中,为格点三角形,即顶点A、B、C均在格点上,利用无刻度直尺按要求完成下列各题,并保留作图痕迹;
(1)请在图①中AB边上找一点M,使;
(2)请在图②中内部(不含边界)找一点N,使.
20.(8分)东城区为了解各学校中学生在疫情期间体育锻炼的情况,对甲、乙两个学校各180名学生进行了体育测试,从中各随机抽取30名学生的成绩(百分制),并对成绩(单位:分)进行整理、描述和分析.给出了部分成绩信息.
甲校参与测试的学生成绩分布如表:
成绩(分)
甲校 2 3 5 10 10
甲校参与测试的学生成绩在这一组的数据是:
96,96.5,97,97.5,96.5,96.5,97.5,96,96.5,96.5
甲、乙两校参与测试的学生成绩的平均数、中位数、众数如表,根据以上信息,回答下列问题:
学校 平均数 中位数 众数
甲校 96.35 m 99
乙校 95.85 97.5 99
(1)______;
(2)在此次随机抽样测试中,甲校的王同学和乙校的李同学成绩均为97分,则在各自学校参与测试同学中成绩的名次相比较更靠前的是______(填“王”或“李”)同学,请简要说出理由;
(3)在此次随机测试中,乙校大于96分的总人数比甲校大于96分的总人数的2倍少100人,试估计乙校大于96分的总人数.
21.(8分)如图(1),和是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道上从处出发,到达后,以同样的速度返回处,然后重复上述过程;乙在赛道上以1.5 m/s的速度从处出发,到达后以相同的速度回到处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设到池边的距离为y(m),如图2表示甲到池边的距离y(m)与t(s)的函数图象.
(1)赛道的长度是______m,甲的速度是______m/s;
(2)当时,求甲到池边的距离y(m)与t(s)的函数关系式.
(3)第三次相遇时,两人距池边多少米.
22.(9分)【探究】在一次数学课上,老师出示了这样一道题目:“如图,在矩形ABCD中,AC为对角线,,E、F分别为边BC、AD上的点,连结AE、CF,分别将和沿AE、CF翻折,使点B、D的对称点G、H都落在AC上.求证:四边形AECF是平行四边形.”以下是两名学生的解题方法:
甲学生的方法是:首先由矩形的性质和轴对称的性质证得,,,,易得,可得(ASA),由平行四边形的判定定理可得结论.乙学生的方法是:不利用三角形全等知识,依据平行四边形的定义证明.
(1)甲学生证明四边形AECF是平行四边形所用的判定定理的内容是_______________________.
(2)用乙学生的方法完成证明过程.
【应用】当学生们完成证明后,老师又提出了一个问题:
若四边形AECF是菱形,则的值为______.
23.(10分)如图,在中,,,,点P从A出发,沿AC方向以每秒1个单位长度的速度向终点C运动.当点P不与点A、C重合时,将线段AP绕点P逆时针旋转90°,得到线段PQ,以PC、PQ为边作矩形PQHC、点H恰好落在直线BC上.设矩形PQHC与重叠部分的图形面积为S(平方单位),点P的运动时间为t(秒).
(1)证明矩形PQHC的周长是一个定值.
(2)当矩形PQHC为正方形时,求t的值.
(3)在整个运动过程中,存在全等三角形时,求S的值.
(4)矩形PQHC的对角线PH和CQ的交点为M,作点Q关于直线AB的对称点N,当MN与的边平行或者垂直时,直接写出此时的t值.
24.(12分)在平面直角坐标系xOy中,抛物线(b、c为常数)经过点和点,点M在此抛物线上,点M的横坐标为m,点M不与A、B重合.
(1)求此抛物线所对应的函数表达式.
(2)当,求点M的坐标.
(3)作点A关于抛物线对称轴的对称点为点C,当点M到直线AC的距离是点M到x轴距离2倍时,求m的值.
(4)设点E的坐标为,点F的坐标为,连结EF.当抛物线在B、M两点之间的部分(包含B、M两点)与线段EF有1个公共点时,直接写出m的取值范围.
同课章节目录
