认识三角形[下学期]
图片预览

文档简介
关于三角形的一些概念
一、 三角形
1、 定义:三角形是由三条线段“首尾顺次相接”组成的。这里要强调“首尾顺次相接”
2、 三个顶点,三条边(线段)
3、 三角形分类:按角,按边。
二、三角形的边
定理:三角形两边的和大于第三边
推论:三角形两边的差小于第三边
(1)判断三条已知线段能否组成三角形
采用一种较为简便的判法:若最短边与较长边的和大于最长边,则可构成三角形,否则不能.
(2)确定三角形第三边的取值范围:两边之差<第三边<两边之和
例1 判断题
(1)等边三角形是等腰三角形
(2)三角形可分为不等边三角形、等腰三角形和等边三角形
(3)已知三线段 满足 ,那么 为边可构成三角形
(4)等腰三角形的腰比底长
例3 一个等腰三角形的周长为18 .
(1) 已知腰长是底边长的2倍,求各边长.
(2) 其中一边长4 cm,求其他两边长.
例4 草原上有4口油井,位于四边形ABCD的4个顶点,如图1现在要建一个维修站H,试问H建在何处,才能使它到4口油井的距离HA+HB+HC+HD为最小,说明理由.
思考题:1、在四边形ABCD中,AC与BD相交于P,求证:
(AB+BC+CD+AD)/2<AC+BD<AB+BC+CD+AD
2、用15根等长的火柴棒摆成的三角形中,最长边最多可以由几根火柴棒组成?
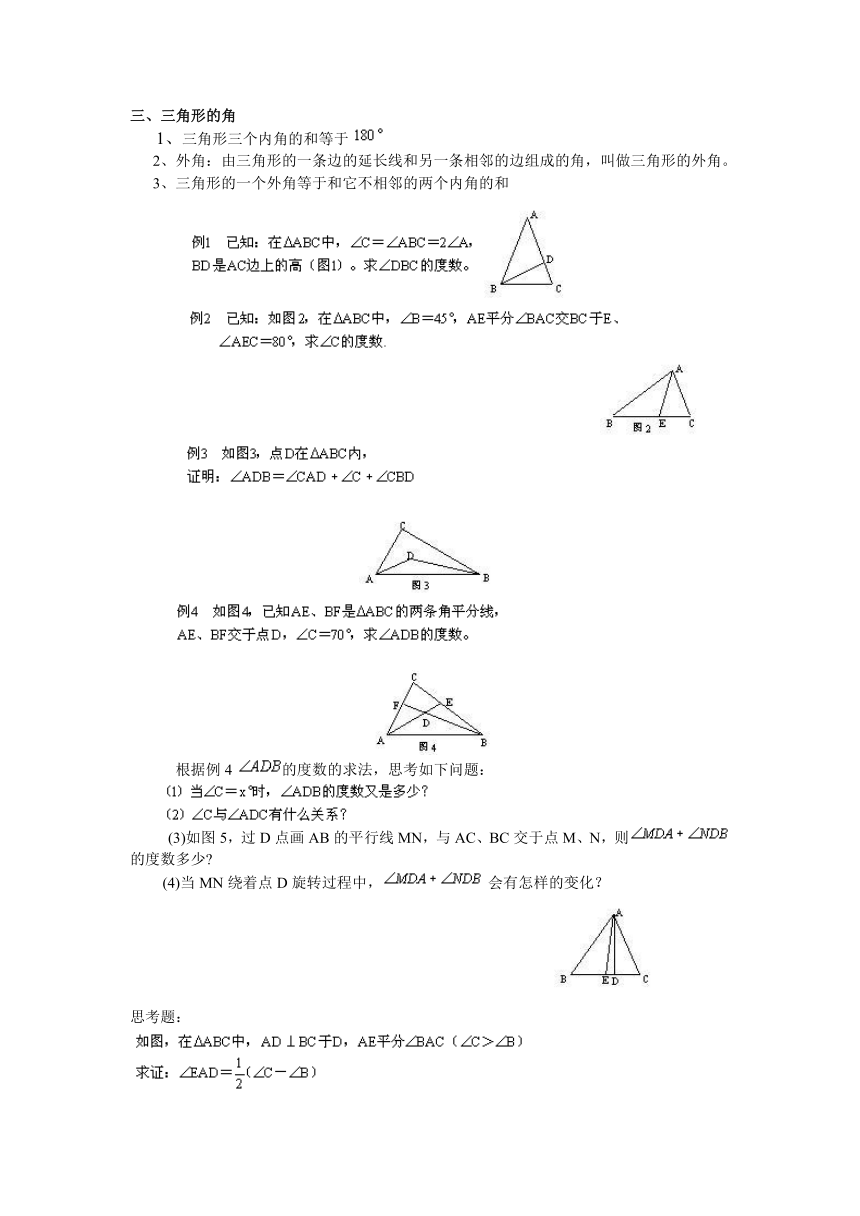
三、三角形的角
1、三角形三个内角的和等于
2、外角:由三角形的一条边的延长线和另一条相邻的边组成的角,叫做三角形的外角。
3、三角形的一个外角等于和它不相邻的两个内角的和
根据例4 的度数的求法,思考如下问题:
(3)如图5,过D点画AB的平行线MN,与AC、BC交于点M、N,则 的度数多少
(4)当MN绕着点D旋转过程中, 会有怎样的变化?
思考题:
四、三角形的角平分线
定义:三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段。强调:三角形的角平分线是一条线段,而角的平分线是一条射线。
角平分线的性质定理:在角平分线上的点到这个角两边距离相等。
强调说明:(1)、定理的条件及结论的符号表示;
(2)、定理的作用:直接证明两线段相等。使用的前提是有角的平分线,关键是图中是
否有“垂直”。
逆定理:到一个角的两边距离相等的点,在这个角的平分线上。
例1、已知:如图1,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
例2、已知:如图2,PB、PC分别是△ABC的外角平分线,相交于点P.求证:P在∠A的平分线上
例3、已知:如图3,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点求证:∠BDP=∠CDP
思考题:
(1)已知:如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC.
求证:∠A+∠C=
(2)求证三角形的三条内角平分线交于一点。
如图,公路南有一学校在铁路的东侧,到公路的距离与到铁路的距离相等,并且与两路交叉
处O的距离为400米,在图上标出学校的位置,并说明理由(比例尺1:10000)。
五、三角形的高
定义:三角形的高:从三角形的一个顶点向它对边画垂线,顶点和垂足间的线段。
强调:三角形的高是线段,而垂线是直线。任何三角形都有三条高。
题1 三角形的一条高是( )
A.直线 B.射线 C.垂线 .D.垂线段
题2 画钝角三角形 的高AE。
题3
六、三角形的中线
定义:三角形的中线:在三角形中,连结一个顶点和它的对边中点的线段。
强调:三角形中线是一条线段。
如图1:试画出 的平分线、BC边上的中线、BC边上的高
思考题1:
思考题2:
探究活动
1、以3根火柴为边,可以组成一个三角形,用6根火柴为边最多可以组成几个三角形 9根火柴最多能组成几个三角形?
2、从三角形一个顶角引出的三角形角平分线、一条中线能否重合?此时这个三角形的形状如何?
一、 三角形
1、 定义:三角形是由三条线段“首尾顺次相接”组成的。这里要强调“首尾顺次相接”
2、 三个顶点,三条边(线段)
3、 三角形分类:按角,按边。
二、三角形的边
定理:三角形两边的和大于第三边
推论:三角形两边的差小于第三边
(1)判断三条已知线段能否组成三角形
采用一种较为简便的判法:若最短边与较长边的和大于最长边,则可构成三角形,否则不能.
(2)确定三角形第三边的取值范围:两边之差<第三边<两边之和
例1 判断题
(1)等边三角形是等腰三角形
(2)三角形可分为不等边三角形、等腰三角形和等边三角形
(3)已知三线段 满足 ,那么 为边可构成三角形
(4)等腰三角形的腰比底长
例3 一个等腰三角形的周长为18 .
(1) 已知腰长是底边长的2倍,求各边长.
(2) 其中一边长4 cm,求其他两边长.
例4 草原上有4口油井,位于四边形ABCD的4个顶点,如图1现在要建一个维修站H,试问H建在何处,才能使它到4口油井的距离HA+HB+HC+HD为最小,说明理由.
思考题:1、在四边形ABCD中,AC与BD相交于P,求证:
(AB+BC+CD+AD)/2<AC+BD<AB+BC+CD+AD
2、用15根等长的火柴棒摆成的三角形中,最长边最多可以由几根火柴棒组成?
三、三角形的角
1、三角形三个内角的和等于
2、外角:由三角形的一条边的延长线和另一条相邻的边组成的角,叫做三角形的外角。
3、三角形的一个外角等于和它不相邻的两个内角的和
根据例4 的度数的求法,思考如下问题:
(3)如图5,过D点画AB的平行线MN,与AC、BC交于点M、N,则 的度数多少
(4)当MN绕着点D旋转过程中, 会有怎样的变化?
思考题:
四、三角形的角平分线
定义:三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段。强调:三角形的角平分线是一条线段,而角的平分线是一条射线。
角平分线的性质定理:在角平分线上的点到这个角两边距离相等。
强调说明:(1)、定理的条件及结论的符号表示;
(2)、定理的作用:直接证明两线段相等。使用的前提是有角的平分线,关键是图中是
否有“垂直”。
逆定理:到一个角的两边距离相等的点,在这个角的平分线上。
例1、已知:如图1,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
例2、已知:如图2,PB、PC分别是△ABC的外角平分线,相交于点P.求证:P在∠A的平分线上
例3、已知:如图3,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点求证:∠BDP=∠CDP
思考题:
(1)已知:如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC.
求证:∠A+∠C=
(2)求证三角形的三条内角平分线交于一点。
如图,公路南有一学校在铁路的东侧,到公路的距离与到铁路的距离相等,并且与两路交叉
处O的距离为400米,在图上标出学校的位置,并说明理由(比例尺1:10000)。
五、三角形的高
定义:三角形的高:从三角形的一个顶点向它对边画垂线,顶点和垂足间的线段。
强调:三角形的高是线段,而垂线是直线。任何三角形都有三条高。
题1 三角形的一条高是( )
A.直线 B.射线 C.垂线 .D.垂线段
题2 画钝角三角形 的高AE。
题3
六、三角形的中线
定义:三角形的中线:在三角形中,连结一个顶点和它的对边中点的线段。
强调:三角形中线是一条线段。
如图1:试画出 的平分线、BC边上的中线、BC边上的高
思考题1:
思考题2:
探究活动
1、以3根火柴为边,可以组成一个三角形,用6根火柴为边最多可以组成几个三角形 9根火柴最多能组成几个三角形?
2、从三角形一个顶角引出的三角形角平分线、一条中线能否重合?此时这个三角形的形状如何?
