三角形[下学期]

第四章 三角形
一、基础知识梳理
（一）主要概念
1．三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形．
三个内角都是锐角的三角形叫做锐角三角形；有一个内角是直角的三角形叫做直角三角形；有一个内角是钝角的三角形叫做钝角三角形．
在三角形中，一个内角的角平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线．
在三角形中，连接一个顶点与它对边中点的线段，叫做这个三角形的中线．从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高线，简称三角形的高．
2．全等图形：两个能够重合的图形称为全等图形．
（二）主要性质
1．三角形任意两边之和大于第三边．
2．三角形任意两边之差小于第三边．
3．三角形三个内角的和等于180°．
4．直角三角形的两个锐角互余．
5．三角形的三条角平分线交于一点，三条中线交于一点，三条高所在的直线交于一点．
6．全等图形的形状和大小都相同．
7．全等三角形的对应边相等，对应角相等．
8．三边对应相等的两个三角形全等，简写为“边边边”或“SSS”．
9．两角和它们的夹边对应相等的两个三角形全等，简写成“角边角”或“ASA”．
10．两角和其中一角的对边应相等的两个三角形全等，简写成“角角边”或“AAS”．
11．两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”．
12．斜边和一条直角边对应相等的两个直角三角形全等，简写成“斜边、直角边”或“HL”．
（三）三角形的三条主要线段的区别和联系
区别 相同点
中线 平分对边 三角形内部 （1）都是线段（2）都从顶点画出（3）所有直线交于一点
角平分线 平分内角 三角形内部
高线 垂直于对边 （或其延长线） 锐角三角形：内部
直角三角形： 两条高线恰好是直角边
钝角三角形：两条高线在外部
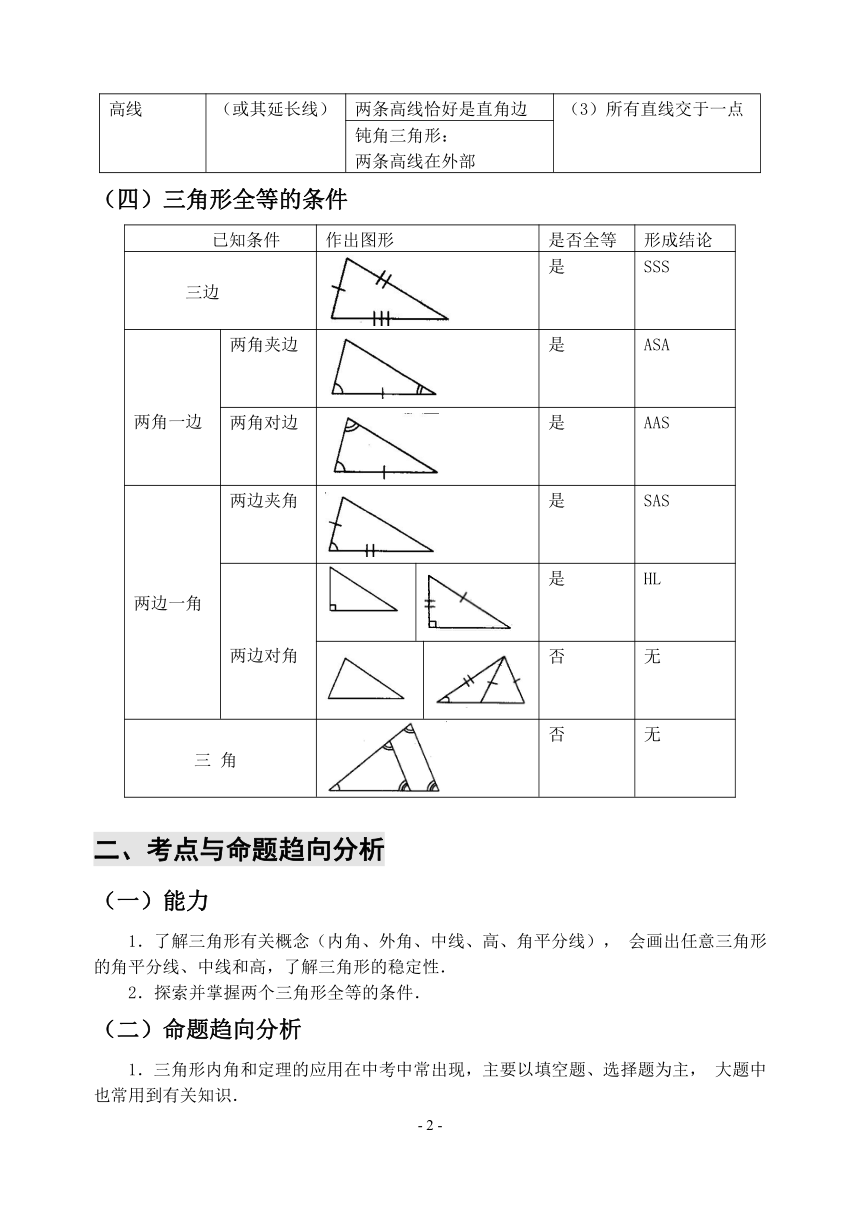
（四）三角形全等的条件
已知条件 作出图形 是否全等 形成结论
三边 是 SSS
两角一边 两角夹边 是 ASA
两角对边 是 AAS
两边一角 两边夹角 是 SAS
两边对角 是 HL
否 无
三 角 否 无
二、考点与命题趋向分析
（一）能力
1．了解三角形有关概念（内角、外角、中线、高、角平分线），会画出任意三角形的角平分线、中线和高，了解三角形的稳定性．
2．探索并掌握两个三角形全等的条件．
（二）命题趋向分析
1．三角形内角和定理的应用在中考中常出现，主要以填空题、选择题为主，大题中也常用到有关知识．
2．三角形的全等在大题中常常配合其他知识出现．
【例】（2003年云南）如图所示，∠α=125°，∠1=50°，则∠β的度数是_____．
【分析】本题考查三角形外角和邻补角定义．
【解】∵∠α+3=180°（平角定义）
∠1+∠2+∠3=180°（三角形内角和等于180°）
∴∠α＝∠1+∠2
∴∠2=∠α-∠1=125°－50°＝75°
∴∠β＝180°－∠2=180°－75°＝105°（平角定义）
三、解题方法与技巧
方法1：变换与转化思想
在证明两个角相等或两条线段相等时，可以把要证的两个角或线段放在两个三角形中，把证角或线段相等的问题转化成证明两个三角形全等的问题．有些问题可以尝试作几何辅助线，把题设与结论联系起来，使复杂问题转化成简单问题，把实际问题转化成数学模型来解决．
【例1】如图，已知在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD．求证：AB=CF.
【分析】AB与CF分别是△ABD和△CFD的斜边，因此可证明这两个三角形全等．
【证明】∵AD⊥BC，CE⊥AB
∴∠1+∠B=∠2+∠B=90°
∴∠1=∠2
在Rt△ABD和Rt△CFD中，
∵∠1=∠2，AD=CD，∠3=∠4=90°
∴△ABD≌△CFD
∴AB=CF
【规律总结】1．在证明两线段相等时，如果两线段分别为某两个三角形的边时，转化为证两个三角形全等．
2．一个三角形有两条高线时，要注意找同角（或等角）的余角相等．如图4-2中的∠1=∠2．
方法2：倍长中线法
【例2】已知：如图，在△ABC中，AD是BC边上的中线，AB=8，AC=6，求AD的取值范围．
【分析】要求的线段AD与两条已知线段AB、AC有共同的端点A，不能构成三角形，加倍延长AD到M，连结BM，则AB、BM、2AD构成三角形．
【解】延长AD到M，使DM=AD．连结BM．则AM=2AD．
在△ADC和△MDB中．
∴△ADC≌△MDB（SAS）
∴BM=CA=6（全等三角形对应边相等）
在△ABM中
AB-BM∴8-6<2AD<8+6
∴1【规律总结】当已知条件中有中点这个条件时，常倍长中线．将位于中线两旁的两条边，两个角集中于同一个三角形之中，以利于问题的解决．
方法3：方程的思想
【例3】如图，AB=12米，CA⊥AB于A，BD⊥AB于B，且AC=4米，P点从B向A运动每分钟走1米，Q点从B向D运动每分钟走2米，P、Q两点同时出发，运动几分钟后，△CAP≌△PQB，试说明理由．
【分析】如果△CAP≌△PQB，那么边的等量关系有两种可能．
（1）AC=BQ，AP=BP； （2）AC=PB，AP=BQ．
【解】设运动x分后，△CAP≌△PQB，
则BP=x（米），BQ=2x（米），那么AP=（12-x）（米）
∵ ① 或②
①无解，②的解为x=4．
∴P、Q运动4分钟后，△CAP≌△PQB
【规律总结】本题通过设未知数列方程求解，体现了变量间的关系，运用了方程的思想方法．
方法4：利用分析法找到解题思路，再用综合法加以叙述
【例4】已知：如图，AB∥DE，DF=EC，∠A=∠D．
求证：AC=DF.
【分析】要证AC=DF
只要证△ABC≌△DEF，∵∠A=∠D
∴只要证∠B=∠E和BC=EF，
由已知AB∥DE，可证∠B=∠E
由已知BF=EC，可证BC=EF
所以可证△ABC≌△DEF，从而证得AC=DF．
【证明】略，证明过程只需反推过去．
【规律总结】分析法和综合法是相辅相成的，一般先用分析法找到解题思路，然后用综合法加以叙述．
方法5：观察与实验
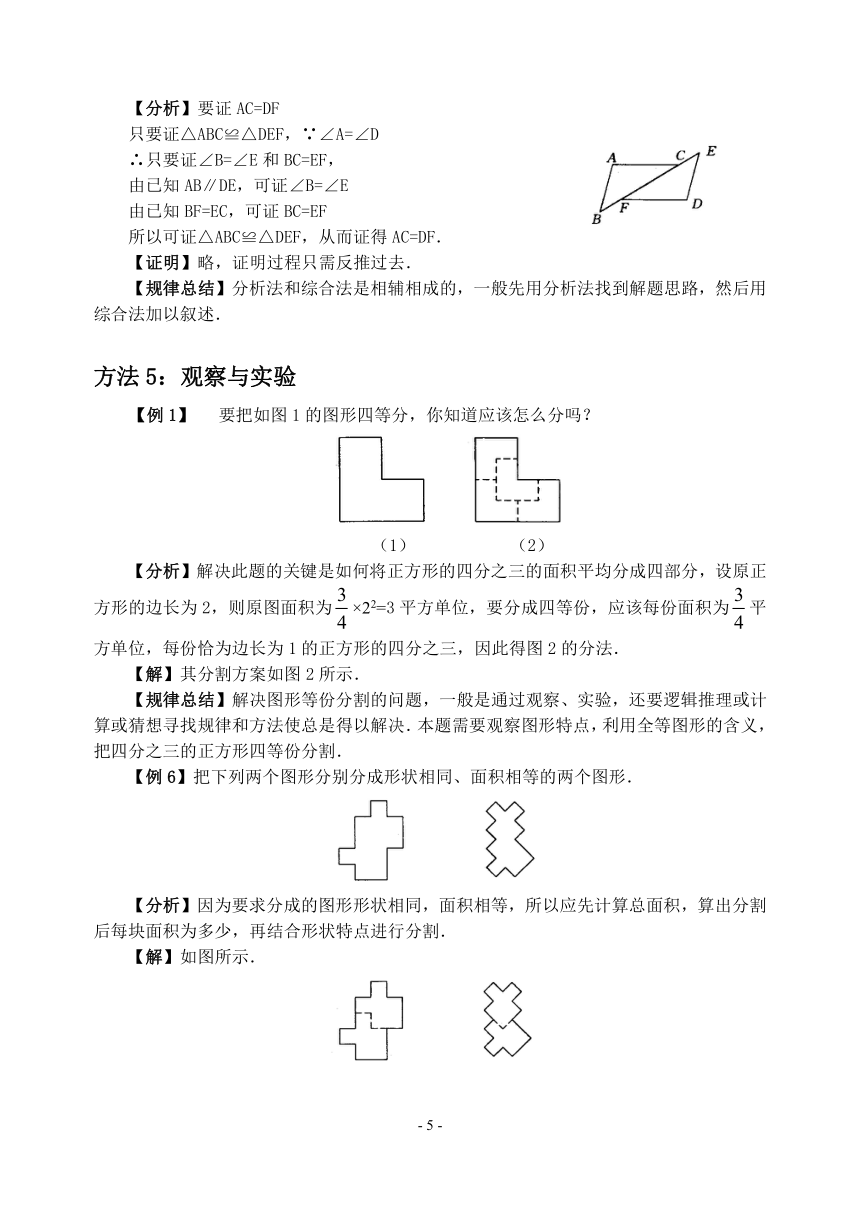
【例1】 要把如图1的图形四等分，你知道应该怎么分吗？
（1） （2）
【分析】解决此题的关键是如何将正方形的四分之三的面积平均分成四部分，设原正方形的边长为2，则原图面积为×22=3平方单位，要分成四等份，应该每份面积为平方单位，每份恰为边长为1的正方形的四分之三，因此得图2的分法．
【解】其分割方案如图2所示．
【规律总结】解决图形等份分割的问题，一般是通过观察、实验，还要逻辑推理或计算或猜想寻找规律和方法使总是得以解决．本题需要观察图形特点，利用全等图形的含义，把四分之三的正方形四等份分割．
【例6】把下列两个图形分别分成形状相同、面积相等的两个图形．
【分析】因为要求分成的图形形状相同，面积相等，所以应先计算总面积，算出分割后每块面积为多少，再结合形状特点进行分割．
【解】如图所示．
四、中考试题归类解析
（一）三角形概念与三边关系定理的运用
【例1】（2004，嘉兴）小华要从长度分别为5cm，6cm，11cm，16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是_________．
【思路分析】本题主要考查三角形三条边的关系，由三角形三边关系可知，只有6cm，11cm，16cm能构成一个三角形．
【解】答案：6cm，11cm，16cm
【规律总结】一般判断三条线段能否构成三角形方法是利用“两边之和大于第三边，两边之差小于第三边”来判断．
【例2】（2004，北京）如图，在△ACB中，∠ACB=90°，CD⊥AB，垂足为D，若∠B=30°，CD=6，求AB的长．
【思路分析】利用三角函数由∠B=30°，CD=6可求出CB，再由CB与∠B可求出AB．
【解】在Rt△BDC中
sin∠B=
BC===12
在Rt△ABC中：cos∠B= AB===8
【规律总结】本题方法很多，但利用三角函数来解比较简单．
（二）全等三角形
【例1】（2003，湛江）如图，∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：
①∠1=∠2 ②BE=CF △ACN≌△ABM ④CD=DN。其中正确的结论是_________．
【思路分析】由∠E＝∠F，∠B=∠C，AE=AF可判定△AEB≌△AFC，
从而得∠EAB=∠FAC．
∴∠1=∠2，又可证出△AEM≌△AFN．
依次类推得①，②，③
【解】答案：①②③
【规律总结】注意已知条件与隐含条件相结合．
【例2】（2004，呼和浩特）如图，已知AC=DB，要使△ABC≌△DCB只需增加的一个条件是________或________．
【思路分析】按着判定两个三角形全等的所有定理进行补充条件即可．
【解】可增加的一个条件是：
①AB=DC ②∠ACB=∠DBC
【规律总结】要准确写出补充的一个条件，对于判定三角形全等的定理必需熟知．
（三）作图
【例1】（2003，桂林）正在修建的中山路有一形状如图所示的三角形空地需要绿化，拟从点A出发，将△ABC分成面积相等的三个三角形，以便种上三种不同的花草，请你帮助规划出图案（保留作图痕迹，不写作法）
【思路分析】要使分割的三个三角形面积相等，只要把BC三等分就可达到目的．
【解】1．过点B作一射线BM．
2．在射线BM上顺次截取BE=EF=FH．
3．连结CH，过E、F作CH的平行线交BC于P、Q分别连线AP、AQ．
所以△ABP，△APQ，△AQC即为所求．
【规律总结】等底、等高的三角形面积相等在实际问题中经常用到．
【例2】（2004，山西）某服装厂里有大量剩余的等腰直角三角形边角布料，现找出其中的一种，测得∠C=90°，AC=BC（如图），现要从这种三角形中剪出几种不同的扇形，做成不同形状的玩具，求要使扇形的半径恰好在△ABC的边上，且扇形的弧与△ABC的其他边相切．请你在下面备用的等腰直角三角形中，设计出所有符合要求的不同的方案示意图．（要求：尺规作图，不写作法，保留作图痕迹）
【思路分析】要注意两点一是扇形的半径应在三角形的边上；二是扇形弧要与△ABC其他边相切，同时具备．
【解】所设计方案如下图所求.
【规律总结】此题比较典型，我们应该重点记忆所出现的种种情况．
五、中考试题集萃
（一）填空题
1．（2003，隋州）在△ABC，∠A：∠B：∠C=1：2：3，已知BC=3cm，则AB=_______cm．
2．（2003，鄂州）有两条线段的长分别为3和5，第三条线段的长为x，若这三条线段不能构成三角形，则x的取值范围________。
3．（2003，海淀）如图1，点D在AB上，点E在AC上，CD与BE相交于点O，且AD=AE，AB=AC，若∠B=20°，则∠C=______．
（1） (2) (3) (4)
4．（2003，南通）已知等腰三角形的两边边长分别是1cm和2cm，则这个等腰三角形的周长为_______cm．
5．（2003，北京海淀）若三角形的两边长分别6和7，则第三边长a的取值范围是________．
6．（2003，福州）如果等腰三角形的一个底角是80°，那么顶角是_______度．
7．（2003，河南）如图2，在等腰梯形ABCD中，AD∥BC，AB=DC，CD=BC，E是BA、CD延长线的交点，∠E=40°，则∠ACD=______度．
8．（2003，吉林）如图3，∠1+∠2+∠3+∠4=_________度．
9．（2004，绍兴）如图4，在△ABC中，CD⊥AB，请你添加一个条件，写出一个正确结论（不在图中添加辅助线），条件：_________，结论：____________．
10．（2004，深圳）等腰三角形的两边长分别为2cm和5cm，则它的周长为______．
11．（2004，昆明）在△ABC中，已知AB=AC，∠B=70°，则∠A=_______．
12．（2004，陕西）如图5，有一腰长为5cm，底边长为4cm的等腰三角形纸片，沿着底边上的中线将纸片剪开，得到两个全等的直角三角形纸片，用这两个直三角形低片拼成的平面图形中有________个不同的四边形．
(5) (6)
13．（2004，郴州）如图6，在△ABC和△A′B′C′中，AB=A′B′，∠A=∠A′，要使△ABC≌△A′B′C′，则需增加条件________．（限写一个）
（二）选择题
1．（2003，隋州）已知，如图7，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1=∠2，则图中全等的三角形共有（ ）
A．1对 B．2对 C．3对 D．4对
2．（2003，菏泽）如图8，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数为（ ）
A．45° B．55° C．60° D．75°
(7) (8) (9)
3．（2003，苏州）在△ABC中，若AB=9，BC=6，则第三边CA的长度的取值范围是（ ）
A．34．（2003，昆明）已知等腰三角形的两边长分别为6cm，3cm，则该等腰三角形的周长是（ ）
A．9cm B．12cm C．12cm或15cm D．15cm
5．（2004，北京）如图9，在菱形ABCD中，E是AB的中点，作EF∥BC，交AC于点F，如果EF=4，那么CD的长为（ ）
A．2 B．4 C．6 D．8
6．（2004，哈尔滨）以下列各组线段长为边，能组成三角形的是（ ）
A．1cm，2cm，4cm B．8cm，6cm，4cm
C．12cm，5cm，6cm D．2cm，3cm，6cm
7．（2004，潍坊）如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中和△ABC全等的图形是（ ）
A．甲和乙 B．乙和丙 C．只有乙 D．只有丙
（三）解答题
1．（2003，南充）如图，四边形ABCD中，AB=AD，AC平分∠BCD，AE⊥BC，AF⊥CD，图中有无和△ABE全等的三角形，请说明理由．
2．（2003，哈尔滨）已知，如图，点A、E、F、C在同一条直线上，AD∥BC，AD=CB，AE=CF，求证：BE=DF．
3．（2004，黄冈）如图，已知在△ABC中，AB=AC，△BAC=120°，AC垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF.
4．（2004，宁夏）如图，AB=AD，BC=CD，AC、BD相交于E，由这些条件可以得出若干结论，请你写出其中三个正确结论．（不要添加字母和辅助线，不要求证明）
结论1：
结论2：
结论3：
5．（2004，嘉兴）如图，四边形ABCD中，对角线AC、BD相交于点E，已知：DA=DC，E为AC中点．求证：（1）AC⊥BD；（2）∠ABD=∠CBD.
答案：
一、填空题：
1．6 2．0二、选择题：
1．D 2．C 3．D 4．D 5．D 6．B 7．B
三、解答题：
1．解：图中△ABE≌△ADF
∵∠1=∠2，AE⊥BC AF⊥CD
∴AE=AF
∵AB=AD
∴Rt△ABE≌Rt△ADF（HL）．
2．证明：∵AD∥BC
∴∠A=∠C
又∵AE=CF
∴AF=CE
在△ADF与△CBE中
∴△ADF≌△CBE
∴BE=DF．
3．连接AF，则在△AFC中，AF=FC，且∠CAF=∠C=30°，
∠BAF=∠BAC-∠FAC=90°，在△ABF中，∵AB=AC，∠BAC=120°
∴∠B=∠C=30° ∴∠AFB=180°-∠B-∠FAB=60°
∴AF=BF
∴FC=BF
∴BF=2CF．
4．①CA平分∠DAB;②CA平分∠DCB;③DE=EB
5．证明：（1）∵DA=DC，E为AC中点
∴AC⊥BD
（2）∵AC⊥BD
∴∠AEB=∠CEB=90°
∵AE=CE，BE=BE
∴△AEB≌△CEB
∴∠ABD=∠CBD．
- 1 -