7.4二项分布与超几何分布(课时2)超几何分布 课件(共31张PPT)
文档属性
| 名称 | 7.4二项分布与超几何分布(课时2)超几何分布 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 17:41:53 | ||
图片预览











文档简介
(共31张PPT)
第七章 随机变量及其分布
7.4 二项分布与超几何分布
课时2 超几何分布
学习目标
1.通过具体实例,了解超几何分布及其均值.(数学抽象、数学运算)
2.能用超几何分布解决简单的实际问题.(数学运算、数据分析)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
1.超几何分布模型是一种放回抽样?
[答案] 不是,超几何分布模型是一种不放回抽样.
2.超几何分布模型在形式上有怎样的特点?
[答案] 超几何分布模型在形式上常由较明显的两部分组成,如“男生、女生”,“正品、次品”等.
预学忆思
自主预习·悟新知
LONGCHENG NO.1 MIDDLE SCHOOL
3.你能写出超几何分布的概率表示吗?
[答案] 假设一批产品共有
4.超几何分布的期望公式是什么?
[答案] 超几何分布的期望
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)在产品检验中,超几何分布描述的是放回抽样.( )
×
(2)从4名男演员和3名女演员中随机选出4名演员,其中所选女演员的人数
√
(3)在超几何分布中,只要知道
√
自学检测
2.从装有3个白球、4个红球的箱子中,随机取出3个球,恰好是2个白球、1个红球的概率是
( ).
A.
A
[解析] 由题意得,所求概率为
3.老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1)抽到他能背诵的课文的数量
(2)他能及格的概率.
[解析] (1)
则
所以
(2)他能及格的概率
探究1 超几何分布
已知一箱节能灯共100个,其中有8个次品.
问题1:有放回地随机抽取4个,设抽取的4个产品中次品数为
[答案] 如果采用有放回抽样,那么每次抽到次品的概率均为0.08,且各次抽样的结果相互独立,此时
情境设置
合作探究·提素养
LONGCHENG NO.1 MIDDLE SCHOOL
问题2:如果采用不放回抽样,那么抽取的4个产品中次品数
[答案] 采用不放回抽样,每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合
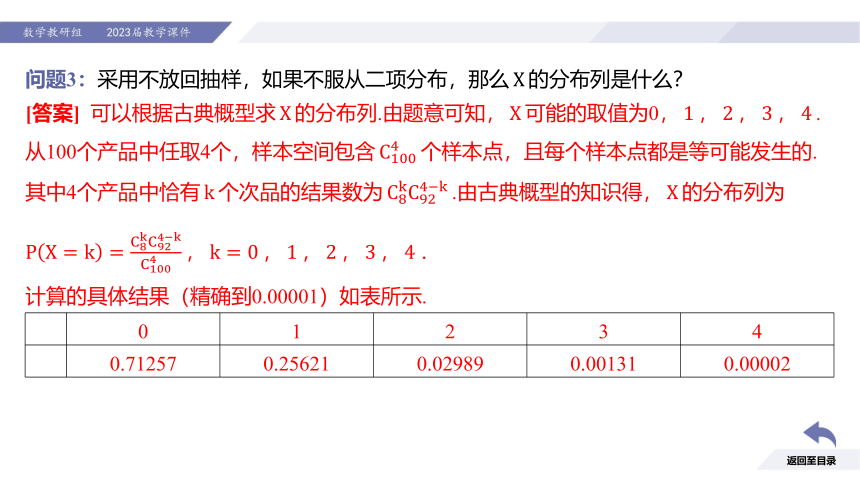
问题3:采用不放回抽样,如果不服从二项分布,那么
[答案] 可以根据古典概型求
计算的具体结果(精确到0.00001)如表所示.
新知生成
超几何分布
一般地,设有
其中
公式中的
若一个随机变量
新知运用
例1 一个袋中装有6个形状大小完全相同的小球,其中红球有3个,编号为1,
(1)求取出的3个球的颜色都不相同的概率;
(2)记取得1号球的个数为随机变量
[解析] (1)从袋中一次随机抽取3个球,基本事件总数
(2)由题意知
方法总结 解决超几何分布问题的两个关键点:
现有10张奖券,其中8张1元的,2张5元的,从中同时任取3张,求所得金额的分布列.
[解析] 设所得金额为
故
巩固训练
探究2 超几何分布的期望
根据国家工信部关于全面推行中国特色企业新型学徒制,加强技能人才培养的通知,我区明确面向各类企业全面推行企业新型学徒制培训,深化产教融合,校企合作,学徒培养以符合企业岗位需要的中、高级技术工人.2022年度某企业共需要学徒制培训200人,培训结束后进行考核,现对考核取得相应岗位证书进行统计,统计情况如下表:
岗位证书 初级工 中级工 高级工 技师 高级技师
人数 20 60 60 40 20
情境设置
问题1:现从这200人中采用分层随机抽样的方式选出10人组成学习技能经验交流团,则交流团中取得技师类(包括技师和高级技师)岗位证书的人数是多少?
[答案] 从200人中采用分层随机抽样的方式选出10人,故抽样比是
故技师和高级技师一共应该抽取的人数是
问题2:再从问题1选出的10人交流团中任意抽出3人作为代表发言,记这3人中技师类的人数为
[答案] 根据问题1中所求可知,10人中有3人是技师,7人是非技师,
则从10人中抽取3人,技师人数
则,
故
所以
故随机变量
问题3:问题2中计算
[答案] 有,
新知生成
超几何分布的期望
新知运用
例2 某厂家生产了两批同种规格的芯片,第一批占
(1)从混合的芯片中任取1个,求这个芯片是合格品的概率;
(2)若在两批产品中采取分层随机抽样的方法抽取一个样本容量为15的样本,再从样本中抽取3片芯片,求这3片芯片含第二批芯片数
[解析] (1)设事件
由全概率公式可知
(2)由题意可知,用分层随机抽样法抽取第一批芯片数是
则
所以
所以
方法总结 超几何分布中,只要知道
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设
巩固训练
[解析] (1)设“选出的3名同学是来自互不相同的学院”为事件
(2)依据条件,随机变量
所以随机变量
所以随机变量
1.在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用
A.
C
[解析] 15个村庄中,7个村庄交通不方便,8个村庄交通方便,
随堂检测·精评价
LONGCHENG NO.1 MIDDLE SCHOOL
2.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量
A.
D
[解析]
3.某10人组成兴趣小组,其中有5名团员,从这10人中任选4人参加某种活动,用
[解析]
4.一个口袋内有
[解析] ∵从口袋中随机取出一个球是红球的概率是
第七章 随机变量及其分布
7.4 二项分布与超几何分布
课时2 超几何分布
学习目标
1.通过具体实例,了解超几何分布及其均值.(数学抽象、数学运算)
2.能用超几何分布解决简单的实际问题.(数学运算、数据分析)
自主预习·悟新知
合作探究·提素养
随堂检测·精评价
1.超几何分布模型是一种放回抽样?
[答案] 不是,超几何分布模型是一种不放回抽样.
2.超几何分布模型在形式上有怎样的特点?
[答案] 超几何分布模型在形式上常由较明显的两部分组成,如“男生、女生”,“正品、次品”等.
预学忆思
自主预习·悟新知
LONGCHENG NO.1 MIDDLE SCHOOL
3.你能写出超几何分布的概率表示吗?
[答案] 假设一批产品共有
4.超几何分布的期望公式是什么?
[答案] 超几何分布的期望
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1)在产品检验中,超几何分布描述的是放回抽样.( )
×
(2)从4名男演员和3名女演员中随机选出4名演员,其中所选女演员的人数
√
(3)在超几何分布中,只要知道
√
自学检测
2.从装有3个白球、4个红球的箱子中,随机取出3个球,恰好是2个白球、1个红球的概率是
( ).
A.
A
[解析] 由题意得,所求概率为
3.老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格.某同学只能背诵其中的6篇,试求:
(1)抽到他能背诵的课文的数量
(2)他能及格的概率.
[解析] (1)
则
所以
(2)他能及格的概率
探究1 超几何分布
已知一箱节能灯共100个,其中有8个次品.
问题1:有放回地随机抽取4个,设抽取的4个产品中次品数为
[答案] 如果采用有放回抽样,那么每次抽到次品的概率均为0.08,且各次抽样的结果相互独立,此时
情境设置
合作探究·提素养
LONGCHENG NO.1 MIDDLE SCHOOL
问题2:如果采用不放回抽样,那么抽取的4个产品中次品数
[答案] 采用不放回抽样,每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合
问题3:采用不放回抽样,如果不服从二项分布,那么
[答案] 可以根据古典概型求
计算的具体结果(精确到0.00001)如表所示.
新知生成
超几何分布
一般地,设有
其中
公式中的
若一个随机变量
新知运用
例1 一个袋中装有6个形状大小完全相同的小球,其中红球有3个,编号为1,
(1)求取出的3个球的颜色都不相同的概率;
(2)记取得1号球的个数为随机变量
[解析] (1)从袋中一次随机抽取3个球,基本事件总数
(2)由题意知
方法总结 解决超几何分布问题的两个关键点:
现有10张奖券,其中8张1元的,2张5元的,从中同时任取3张,求所得金额的分布列.
[解析] 设所得金额为
故
巩固训练
探究2 超几何分布的期望
根据国家工信部关于全面推行中国特色企业新型学徒制,加强技能人才培养的通知,我区明确面向各类企业全面推行企业新型学徒制培训,深化产教融合,校企合作,学徒培养以符合企业岗位需要的中、高级技术工人.2022年度某企业共需要学徒制培训200人,培训结束后进行考核,现对考核取得相应岗位证书进行统计,统计情况如下表:
岗位证书 初级工 中级工 高级工 技师 高级技师
人数 20 60 60 40 20
情境设置
问题1:现从这200人中采用分层随机抽样的方式选出10人组成学习技能经验交流团,则交流团中取得技师类(包括技师和高级技师)岗位证书的人数是多少?
[答案] 从200人中采用分层随机抽样的方式选出10人,故抽样比是
故技师和高级技师一共应该抽取的人数是
问题2:再从问题1选出的10人交流团中任意抽出3人作为代表发言,记这3人中技师类的人数为
[答案] 根据问题1中所求可知,10人中有3人是技师,7人是非技师,
则从10人中抽取3人,技师人数
则
故
所以
故随机变量
问题3:问题2中计算
[答案] 有,
新知生成
超几何分布的期望
新知运用
例2 某厂家生产了两批同种规格的芯片,第一批占
(1)从混合的芯片中任取1个,求这个芯片是合格品的概率;
(2)若在两批产品中采取分层随机抽样的方法抽取一个样本容量为15的样本,再从样本中抽取3片芯片,求这3片芯片含第二批芯片数
[解析] (1)设事件
由全概率公式可知
(2)由题意可知,用分层随机抽样法抽取第一批芯片数是
则
所以
所以
方法总结 超几何分布中,只要知道
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设
巩固训练
[解析] (1)设“选出的3名同学是来自互不相同的学院”为事件
(2)依据条件,随机变量
所以随机变量
所以随机变量
1.在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用
A.
C
[解析] 15个村庄中,7个村庄交通不方便,8个村庄交通方便,
随堂检测·精评价
LONGCHENG NO.1 MIDDLE SCHOOL
2.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量
A.
D
[解析]
3.某10人组成兴趣小组,其中有5名团员,从这10人中任选4人参加某种活动,用
[解析]
4.一个口袋内有
[解析] ∵从口袋中随机取出一个球是红球的概率是
