2023-2024学年湘教版数学九年级上册第1章 反比例函数 章末复习(共18张PPT)
文档属性
| 名称 | 2023-2024学年湘教版数学九年级上册第1章 反比例函数 章末复习(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-09 22:23:41 | ||
图片预览





文档简介
(共18张PPT)
湘教版·九年级数学上册
章末复习
小结复习
1. 举例说明什么是反比例函数.
2. 分别画出当 k>0,k<0时,反比例函数 (k为常数)
的大致图象,并说说反比例函数图象的性质.
3. 请你举出一些生活中应用反比例函数的实例.
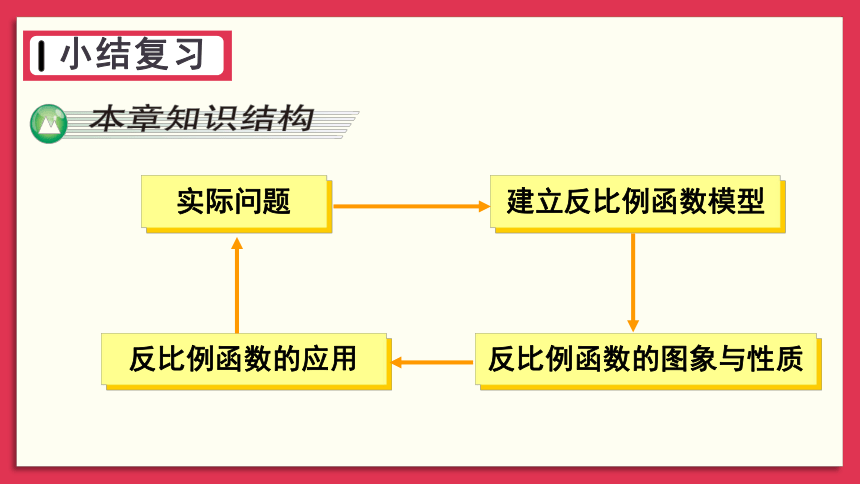
小结复习
实际问题
建立反比例函数模型
反比例函数的图象与性质
反比例函数的应用
巩固练习
1.写出下列函数的表达式,并指出其中哪些是反比例函数.
(1)等边三角形的面积 S (cm2)关于其边长a (cm)的函数;
(2)当平行四边形的面积S (cm2)一定时,它的一条边长 a (cm)关于这条边上的高 h (cm)的函数.
[选自教材P21 复习题1 A组 第1题]
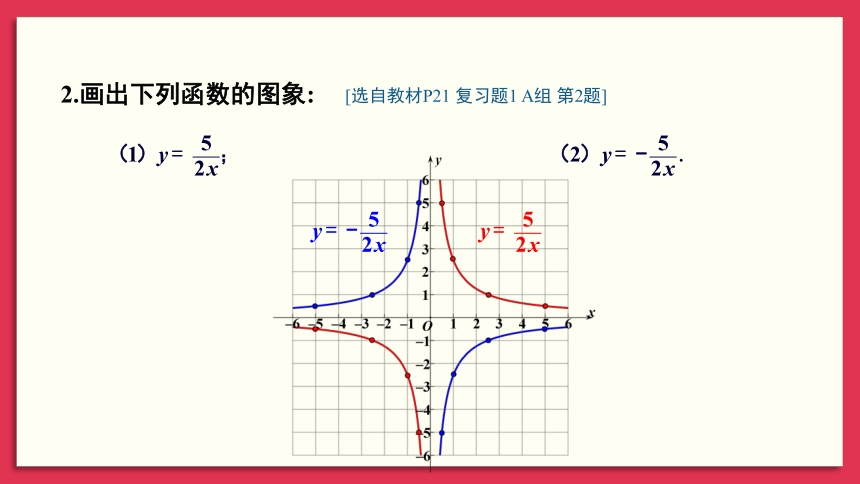
2.画出下列函数的图象:
[选自教材P21 复习题1 A组 第2题]
3.(1)已知点 P (3,-4)在反比例函数 的图象上,求k的值;
(2)已知点 M (7,b)在反比例函数 的图象上,求b的值.
解:(1)
(2)
[选自教材P21 复习题1 A组 第3题]
4.下列哪些点在反比例函数 的图象上,哪些点在反比例函数
的图象上
(1)A(2,7.5); (2)B(-3,5);
(3)C(-5,-3); (4)D(3,5).
[选自教材P21 复习题1 A组 第4题]
解:点A(2,7.5),C(-5,-3),D(3,5)在反比例函数 的图象上,点B(-3,5),在反比例函数 的图象上.
5.已知物体的质量m(kg)、密度ρ(kg/m3)与体积V(m3)满足如下关式:
m= ρV .
(1)当质量m一定时,物体的体积V与它的密度ρ之间有怎样的
函数关系
(2)质量均为1 kg 的铁块与泡沫块,哪个体积大 为什么
(已知铁的密度大于泡沫的密度)
解:(1)V是 ρ 的反比例函数, ;
[选自教材P21 复习题1 A组 第5题]
5.已知物体的质量m(kg)、密度ρ(kg/m3)与体积V(m3)满足如下关式:
m= ρV .
(1)当质量m一定时,物体的体积V与它的密度ρ之间有怎样的
函数关系
(2)质量均为1 kg 的铁块与泡沫块,哪个体积大 为什么
(已知铁的密度大于泡沫的密度)
(2)泡沫块体积大.根据反比例函数 性质可知,
由于m=1,而铁的密度大于泡沫的密度,
因此铁块的体积小于泡沫块的体积.
[选自教材P21 复习题1 A组 第5题]
6.已知反比例函数的图象经过点A(-6,-3).
(1)求这个函数的表达式;
(2)点B(4, ),C(2,-5)是否在这个函数的图象上
(3)这个函数的图象位于哪些象限 函数值 y 随自变量 x 的增大如何变化
解:(1) ;
(2)点B在这个函数的图象上,点C不在这个函数的图象上 ;
[选自教材P21 复习题1 A组 第6题]
6.已知反比例函数的图象经过点A(-6,-3).
(1)求这个函数的表达式;
(2)点B(4, ),C(2,-5)是否在这个函数的图象上
(3)这个函数的图象位于哪些象限 函数值 y 随自变量 x 的增大如何变化
解:(3) 的图象位于第一、三象限,在每个象限内函
数值 y 随自变量 x 的增大而减小 ;
[选自教材P21 复习题1 A组 第6题]
7.已知在反比例函数 图象的每一支曲线上,函数值 y 随着自变
量 x 的增大而增大,求 k 的取值范围.
解:根据反比例函数的性质:k<2.
[选自教材P21 复习题1 A组 第7题]
8.已知反比例函数 的图象与正比例函数y=2x的图象交于点(2,4),
求这个反比例函数的表达式,并在同一平面直角坐标系内,画出这
两个函数的图象.
解:反比例函数的表达式: .
[选自教材P21 复习题1 A组 第8题]
9.如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡.改变托盘B与点О的距离,记录相应的托盘B中的砝码质量,得到下表:
(1)把上表中x , y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出这些点,并用一条光滑曲线连接起来;
解:(1)如图
[选自教材P21 复习题1 A组 第9题]
(2)观察所画的图象,猜测 y 与 x 之间的函数关系,求出该函数表达式;
(3)当砝码质量为24 g时,求托盘B与点О的距离;
(4)当托盘B向左移动(不能移动到点O)时,应往托盘B中添加砝码还是减少砝码 为什么
(2)
(3)
[选自教材P21 复习题1 A组 第9题]
(2)观察所画的图象,猜测 y 与 x 之间的函数关系,求出该函数表达式;
(3)当砝码质量为24 g时,求托盘B与点О的距离;
(4)当托盘B向左移动(不能移动到点O)时,应往托盘B中添加砝码还是减少砝码 为什么
(4)由反比例函数 的性质可知,
当x减小时,y应增大. 因此,应往托盘B中添加砝码.
[选自教材P21 复习题1 A组 第9题]
课堂小结
实际问题
建立反比例函数模型
反比例函数的图象与性质
反比例函数的应用
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
湘教版·九年级数学上册
章末复习
小结复习
1. 举例说明什么是反比例函数.
2. 分别画出当 k>0,k<0时,反比例函数 (k为常数)
的大致图象,并说说反比例函数图象的性质.
3. 请你举出一些生活中应用反比例函数的实例.
小结复习
实际问题
建立反比例函数模型
反比例函数的图象与性质
反比例函数的应用
巩固练习
1.写出下列函数的表达式,并指出其中哪些是反比例函数.
(1)等边三角形的面积 S (cm2)关于其边长a (cm)的函数;
(2)当平行四边形的面积S (cm2)一定时,它的一条边长 a (cm)关于这条边上的高 h (cm)的函数.
[选自教材P21 复习题1 A组 第1题]
2.画出下列函数的图象:
[选自教材P21 复习题1 A组 第2题]
3.(1)已知点 P (3,-4)在反比例函数 的图象上,求k的值;
(2)已知点 M (7,b)在反比例函数 的图象上,求b的值.
解:(1)
(2)
[选自教材P21 复习题1 A组 第3题]
4.下列哪些点在反比例函数 的图象上,哪些点在反比例函数
的图象上
(1)A(2,7.5); (2)B(-3,5);
(3)C(-5,-3); (4)D(3,5).
[选自教材P21 复习题1 A组 第4题]
解:点A(2,7.5),C(-5,-3),D(3,5)在反比例函数 的图象上,点B(-3,5),在反比例函数 的图象上.
5.已知物体的质量m(kg)、密度ρ(kg/m3)与体积V(m3)满足如下关式:
m= ρV .
(1)当质量m一定时,物体的体积V与它的密度ρ之间有怎样的
函数关系
(2)质量均为1 kg 的铁块与泡沫块,哪个体积大 为什么
(已知铁的密度大于泡沫的密度)
解:(1)V是 ρ 的反比例函数, ;
[选自教材P21 复习题1 A组 第5题]
5.已知物体的质量m(kg)、密度ρ(kg/m3)与体积V(m3)满足如下关式:
m= ρV .
(1)当质量m一定时,物体的体积V与它的密度ρ之间有怎样的
函数关系
(2)质量均为1 kg 的铁块与泡沫块,哪个体积大 为什么
(已知铁的密度大于泡沫的密度)
(2)泡沫块体积大.根据反比例函数 性质可知,
由于m=1,而铁的密度大于泡沫的密度,
因此铁块的体积小于泡沫块的体积.
[选自教材P21 复习题1 A组 第5题]
6.已知反比例函数的图象经过点A(-6,-3).
(1)求这个函数的表达式;
(2)点B(4, ),C(2,-5)是否在这个函数的图象上
(3)这个函数的图象位于哪些象限 函数值 y 随自变量 x 的增大如何变化
解:(1) ;
(2)点B在这个函数的图象上,点C不在这个函数的图象上 ;
[选自教材P21 复习题1 A组 第6题]
6.已知反比例函数的图象经过点A(-6,-3).
(1)求这个函数的表达式;
(2)点B(4, ),C(2,-5)是否在这个函数的图象上
(3)这个函数的图象位于哪些象限 函数值 y 随自变量 x 的增大如何变化
解:(3) 的图象位于第一、三象限,在每个象限内函
数值 y 随自变量 x 的增大而减小 ;
[选自教材P21 复习题1 A组 第6题]
7.已知在反比例函数 图象的每一支曲线上,函数值 y 随着自变
量 x 的增大而增大,求 k 的取值范围.
解:根据反比例函数的性质:k<2.
[选自教材P21 复习题1 A组 第7题]
8.已知反比例函数 的图象与正比例函数y=2x的图象交于点(2,4),
求这个反比例函数的表达式,并在同一平面直角坐标系内,画出这
两个函数的图象.
解:反比例函数的表达式: .
[选自教材P21 复习题1 A组 第8题]
9.如图,在左边托盘A(固定)中放置一个重物,在右边托盘B(可左右移动)中放置一定质量的砝码,可使得仪器左右平衡.改变托盘B与点О的距离,记录相应的托盘B中的砝码质量,得到下表:
(1)把上表中x , y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出这些点,并用一条光滑曲线连接起来;
解:(1)如图
[选自教材P21 复习题1 A组 第9题]
(2)观察所画的图象,猜测 y 与 x 之间的函数关系,求出该函数表达式;
(3)当砝码质量为24 g时,求托盘B与点О的距离;
(4)当托盘B向左移动(不能移动到点O)时,应往托盘B中添加砝码还是减少砝码 为什么
(2)
(3)
[选自教材P21 复习题1 A组 第9题]
(2)观察所画的图象,猜测 y 与 x 之间的函数关系,求出该函数表达式;
(3)当砝码质量为24 g时,求托盘B与点О的距离;
(4)当托盘B向左移动(不能移动到点O)时,应往托盘B中添加砝码还是减少砝码 为什么
(4)由反比例函数 的性质可知,
当x减小时,y应增大. 因此,应往托盘B中添加砝码.
[选自教材P21 复习题1 A组 第9题]
课堂小结
实际问题
建立反比例函数模型
反比例函数的图象与性质
反比例函数的应用
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
