17.1(1)勾股定理(上课)
文档属性
| 名称 | 17.1(1)勾股定理(上课) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-19 17:25:17 | ||
图片预览





文档简介
课件26张PPT。人教版八年级数学
千古第一定理——勾股定理
勾股定理(1)
勾股定理的命名 1.约2000年前,我国古代算书《周髀算经》中就记载了公
元前1120年我国古人发现的“勾三股四弦五”.当时把
较短的直角边叫做勾,较长的边叫做股,斜边叫做弦.“
勾三股四弦五”的意思是,在直角三角形中, 如果勾为3,
股为4,那么弦为5.这里32 +42 = 52 .人们还发现, 勾为6,
股为8, 弦一定为10.勾为5,股为12, 弦一定为13等.同
样,有62+82=102 ,52+122 =132 ,…,即勾2 +股2 =弦2 .所以,我国称它为勾股定理.
2.西方国家称勾股定理为毕达哥拉斯定理.
毕达哥拉斯(Pythagoras,约公元前580~前500年)是古希
腊杰出的数学家,天文学家,哲学家.他不仅提出了定理,
而且努力探求证明方法.
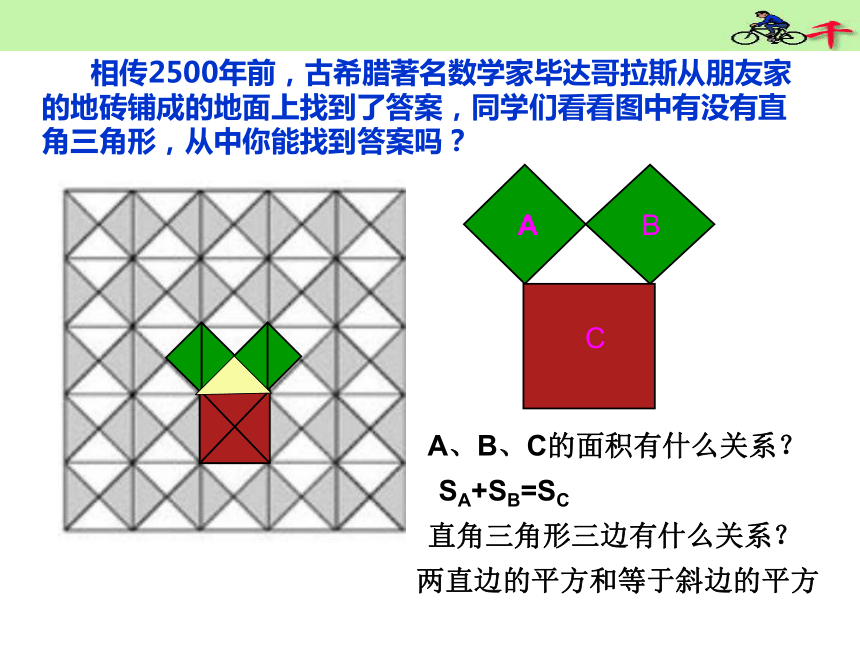
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,我们也来观察下面图中的地面,看看你能发现什么?是否也和大哲学家有同样的发现呢?
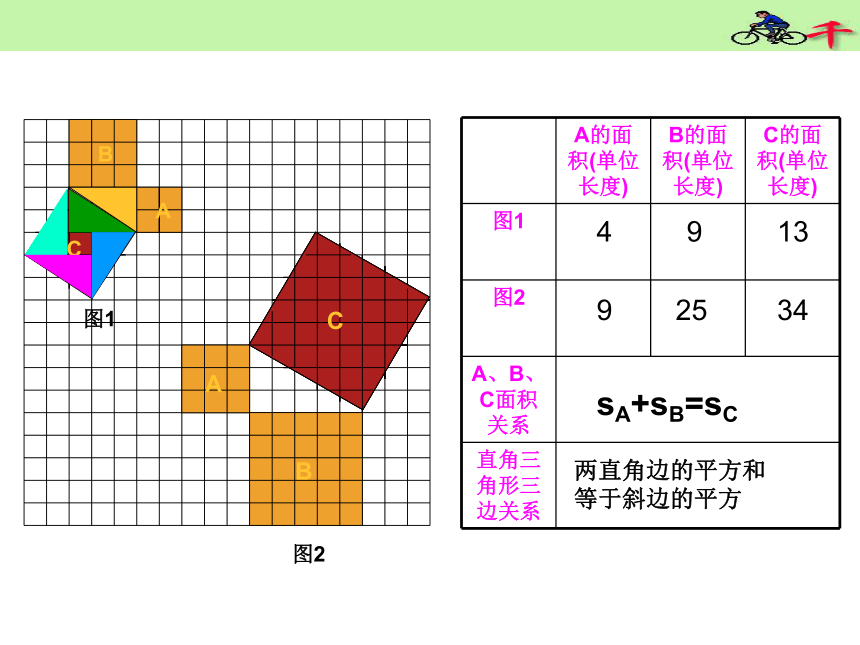
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方ABC图1图2491392534sA+sB=sC两直角边的平方和
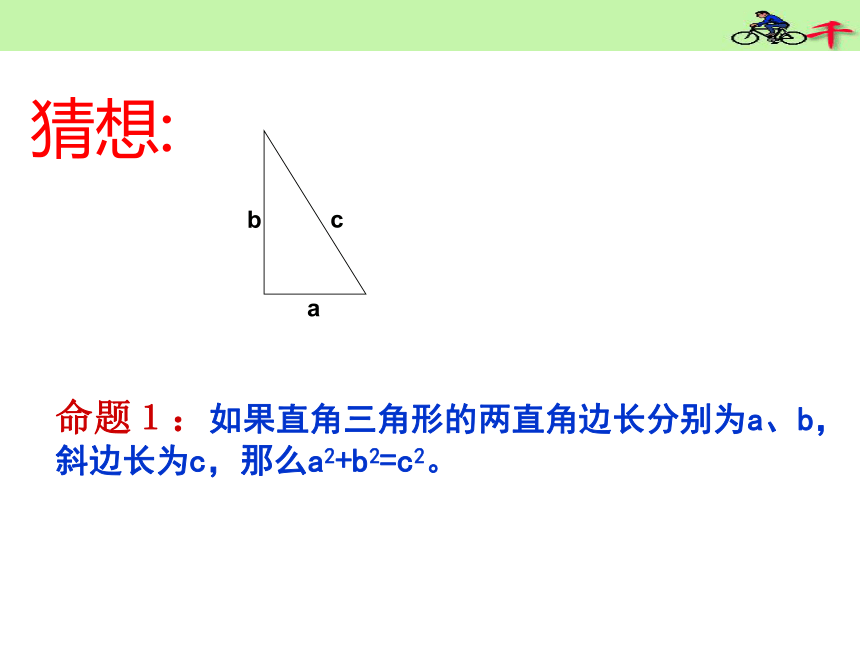
等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。猜想:赵爽的“弦图” 早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
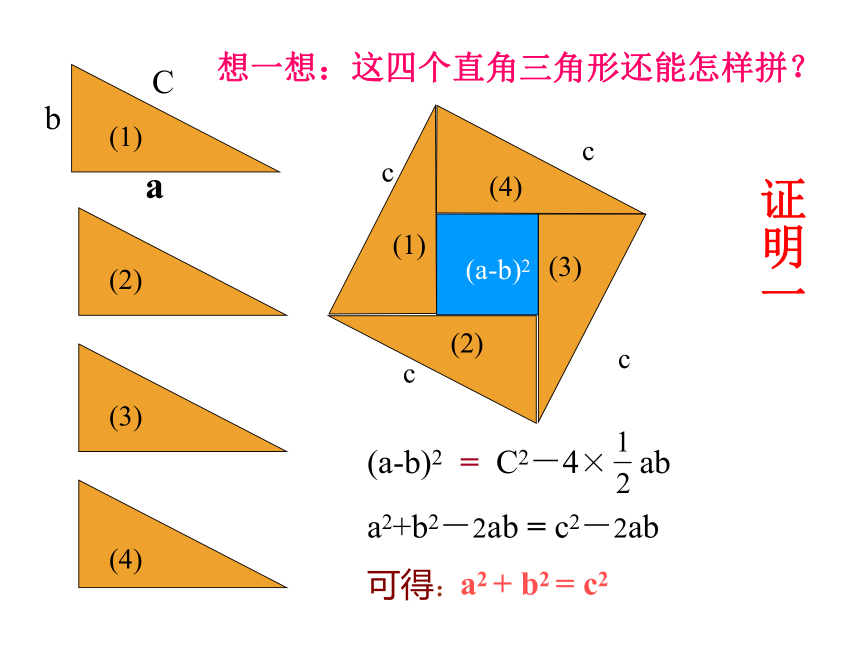
思考:你能验证吗?(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2abbCa想一想:这四个直角三角形还能怎样拼?证明一(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2证明二1、证明:
s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
2、证明:
s大正方形=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+b2
=a2+b2
∵s大正方形=s大正方形
∴c2=a2+b2 3.毕达哥拉斯证法:abcaabbcS大正方形=4× ab+a2+b2
=2ab+a2+b2
S大正方形=4× ab+c2
=2ab+c2
∵S大正方形=S大正方形
∴2ab+a2+b2=2ab+c2
∴a2+b2=c2
定理:经过证明被确认为正确的命题叫做
定理。 勾股定理:如果直角三角形的两直角边长
分别为a、b,斜边为c,那么a2+b2=c2。在我国古代,人们将直角三角形中的短的直角边叫做勾,
长的直角边叫做股,斜边叫做弦.
根据我国古算书《周髀算经》记载,在约公元前1100年,
人们已经知道,如果勾是三,股是四,那么弦是五,
你知道是为什么吗?勾股弦 例 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结⑴已知: a=3, b=4,求c⑵已知: c =10,a=6,求b1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:b815A49B253.求下列图中字母所代表的正方形的面积:学以致用,做一做4.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做做一做: P62540026xP的面积 =______________X=____________225BACAB=__________AC=__________BC=__________2515205, 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 496.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________10 练一练或7、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、12
讨论通过适当添加辅助线构建
直角三角形使用勾股定理. 2.等边△ABC的边长为a,则高AD=
面积S=
384cm21.直角三角形两条直角边的长分别为6和8, 则斜边
上的中线为
2.在Rt△ABC中,∠C=90 ,∠A=30 .则BC:AC:AB=
.
3.在Rt△ABC中,∠C=90 , AC=BC.则AC :BC :AB=
. 若AB=8则AC= .
又若CD⊥AB于D,则CD=
12练习541.勾股定理的内容及证明方法.
2.勾股定理作用:它能把三角形的形的特性(一角为90度)转化为数量关系,即三边满足.
3.利用勾股定理进行计算要注意利用方程的思想求直角三角形有关线段的长.
4.适当添加辅助线构建直角三角形使用勾股定理.小结作业1.阅读课本P79---80
2.P77 1,2,3
勾股定理(1)
勾股定理的命名 1.约2000年前,我国古代算书《周髀算经》中就记载了公
元前1120年我国古人发现的“勾三股四弦五”.当时把
较短的直角边叫做勾,较长的边叫做股,斜边叫做弦.“
勾三股四弦五”的意思是,在直角三角形中, 如果勾为3,
股为4,那么弦为5.这里32 +42 = 52 .人们还发现, 勾为6,
股为8, 弦一定为10.勾为5,股为12, 弦一定为13等.同
样,有62+82=102 ,52+122 =132 ,…,即勾2 +股2 =弦2 .所以,我国称它为勾股定理.
2.西方国家称勾股定理为毕达哥拉斯定理.
毕达哥拉斯(Pythagoras,约公元前580~前500年)是古希
腊杰出的数学家,天文学家,哲学家.他不仅提出了定理,
而且努力探求证明方法.
毕达哥拉斯是古希腊著名的哲学家、数学家、天文学家,相传2500年前,一次,毕达哥拉斯去朋友家作客.在宴席上,其他的宾客都在尽情欢乐,高谈阔论,只有毕达哥拉斯却看着朋友家的方砖地而发起呆来.原来,朋友家的地是用一块块直角三角形形状的砖铺成的,黑白相间,非常美观大方.主人看到毕达哥拉斯的样子非常奇怪,就想过去问他.谁知毕达哥拉斯突破恍然大悟的样子,站起来,大笑着跑回家去了.
同学们,我们也来观察下面图中的地面,看看你能发现什么?是否也和大哲学家有同样的发现呢?
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上找到了答案,同学们看看图中有没有直角三角形,从中你能找到答案吗?A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方ABC图1图2491392534sA+sB=sC两直角边的平方和
等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边长为c,那么a2+b2=c2。猜想:赵爽的“弦图” 早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
思考:你能验证吗?(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2abbCa想一想:这四个直角三角形还能怎样拼?证明一(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2证明二1、证明:
s大正方形=(a+b)2=a2+2ab+b2
s大正方形=c2+4× ab=c2+2ab
∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
2、证明:
s大正方形=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+b2
=a2+b2
∵s大正方形=s大正方形
∴c2=a2+b2 3.毕达哥拉斯证法:abcaabbcS大正方形=4× ab+a2+b2
=2ab+a2+b2
S大正方形=4× ab+c2
=2ab+c2
∵S大正方形=S大正方形
∴2ab+a2+b2=2ab+c2
∴a2+b2=c2
定理:经过证明被确认为正确的命题叫做
定理。 勾股定理:如果直角三角形的两直角边长
分别为a、b,斜边为c,那么a2+b2=c2。在我国古代,人们将直角三角形中的短的直角边叫做勾,
长的直角边叫做股,斜边叫做弦.
根据我国古算书《周髀算经》记载,在约公元前1100年,
人们已经知道,如果勾是三,股是四,那么弦是五,
你知道是为什么吗?勾股弦 例 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.方法小结⑴已知: a=3, b=4,求c⑵已知: c =10,a=6,求b1、已知, Rt△ABC 中,a,b为的两条直角边,c为斜边,求:b815A49B253.求下列图中字母所代表的正方形的面积:学以致用,做一做4.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做做一做: P62540026xP的面积 =______________X=____________225BACAB=__________AC=__________BC=__________2515205, 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和S1S2解:∵ SE= 49S1=SA+SBS2=SC+SD∴ SA+SB+SC+SD
= S1+S2 = SE = 496.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________10 练一练或7、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、12
讨论通过适当添加辅助线构建
直角三角形使用勾股定理. 2.等边△ABC的边长为a,则高AD=
面积S=
384cm21.直角三角形两条直角边的长分别为6和8, 则斜边
上的中线为
2.在Rt△ABC中,∠C=90 ,∠A=30 .则BC:AC:AB=
.
3.在Rt△ABC中,∠C=90 , AC=BC.则AC :BC :AB=
. 若AB=8则AC= .
又若CD⊥AB于D,则CD=
12练习541.勾股定理的内容及证明方法.
2.勾股定理作用:它能把三角形的形的特性(一角为90度)转化为数量关系,即三边满足.
3.利用勾股定理进行计算要注意利用方程的思想求直角三角形有关线段的长.
4.适当添加辅助线构建直角三角形使用勾股定理.小结作业1.阅读课本P79---80
2.P77 1,2,3
