第七章随机变量及其分布 章末小结课件(共32张PPT)
文档属性
| 名称 | 第七章随机变量及其分布 章末小结课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-07 18:59:30 | ||
图片预览










文档简介
(共32张PPT)
第七章 随机变量及其分布
第七章章末小结
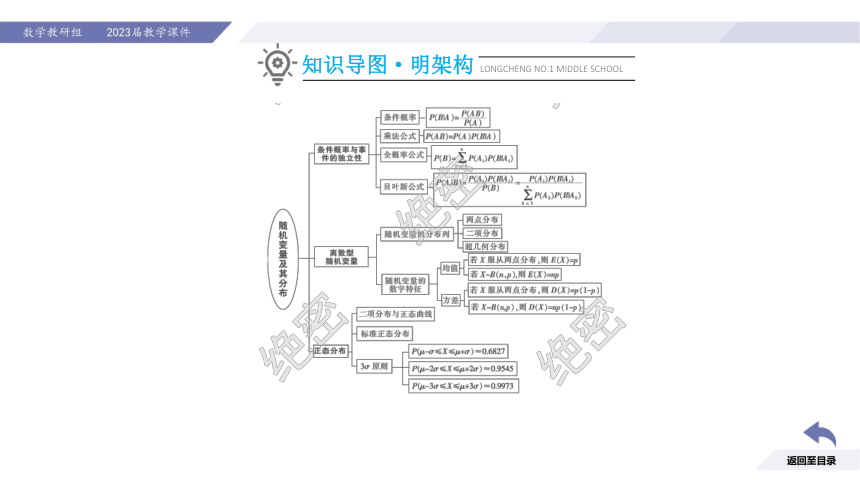
知识导图·明架构
题型探究·悟思路
拓展延伸·育素养
知识导图·明架构
LONGCHENG NO.1 MIDDLE SCHOOL
题型1 条件概率
例1 在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
方法指导 本题是条件概率问题,根据条件概率公式求解即可.
题型探究·悟思路
LONGCHENG NO.1 MIDDLE SCHOOL
[解析] 设“第1次抽到理科题”为事件
(1)从5道题中不放回地依次抽取2道题的事件数为
根据分步乘法计数原理,
于是
(2)因为
(3)(法一)由(1)(2)可得,在第1次抽到理科题的条件下,第2次抽到理科题的概率
(法二)因为
方法总结 求条件概率的主要方法有:(1)利用条件概率公式
题型2 乘法公式与全概率公式
例2 已知甲袋中有3个白球,2个黑球;乙袋中有4个白球,4个黑球.现从甲袋中任取2个球放入乙袋,然后再从乙袋中任取一球,求此球为白球的概率.
[解析] 记事件
记事件
则
由全概率公式可得
方法总结 本题考查利用全概率公式计算事件的概率,解题的关键在于确定从甲袋取出的2个球中白球的个数,结合全概率公式进行计算,本题渗透了数据分析以及数学运算的素养.
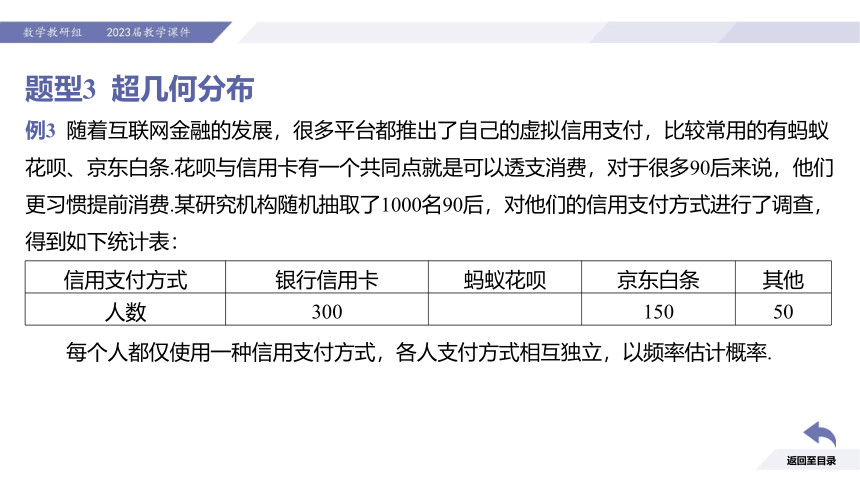
题型3 超几何分布
例3 随着互联网金融的发展,很多平台都推出了自己的虚拟信用支付,比较常用的有蚂蚁花呗、京东白条.花呗与信用卡有一个共同点就是可以透支消费,对于很多90后来说,他们更习惯提前消费.某研究机构随机抽取了1000名90后,对他们的信用支付方式进行了调查,得到如下统计表:
信用支付方式 银行信用卡 蚂蚁花呗 京东白条 其他
人数 300
每个人都仅使用一种信用支付方式,各人支付方式相互独立,以频率估计概率.
(1)估计90后使用蚂蚁花呗的概率;
(2)在所抽取的1000人中用分层随机抽样的方法,先在使用银行信用卡和蚂蚁花呗的人中随机抽取8人,再在这8人中随机抽取4人,记
[解析] (1)
(2)这8人中使用信用卡的人数为
故随机变量
所以,
所以随机变量
故
方法总结 超几何分布的求解步骤:(1)辨模型:结合实际情景分析所求概率分布问题是否具有明显的两部分组成,如“男生、女生”“正品、次品”“优、劣”等.(2)算概率:可以直接借助公式
题型4 独立事件
例4 [2021年新高考全国Ⅰ卷] 有6个相同的球,分别标有数字
A.甲与丙相互独立 B.甲与丁相互独立 C.乙与丙相互独立 D.丙与丁相互独立
B
[解析] 由题意得,
则,
方法总结 求相互独立事件,一般与互斥事件、对立事件结合在一起进行考查,解答此类问题时应分清事件间的内部联系,在此基础上用基本事件之间的交、并、补运算表示出有关事件,并运用相应公式求解.解题过程渗透了数学运算、逻辑推理的素养.
题型5 二项分布
例5 [2021年天津卷] 甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为
[解析] 由题意可得,1次活动中,甲获胜的概率为
则在3次活动中,甲至少获胜2次的概率为
方法总结 解决二项分布问题的两个关注点:(1)对于公式
题型6 离散型随机变量的均值与方差
例6 [2021年新高考全国Ⅰ卷] 某学校组织“一带一路”知识竞赛,有
(1)若小明先回答
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
[解析] (1)由题意可知,
则
所以
(2)由(1)知,小明先回答
若小明先回答
则
所以
因为
方法总结 求离散型随机变量的均值、方差的步骤:
题型7 正态分布
例7 某物理量的测量结果服从正态分布
A.
B.该物理量一次测量结果大于10的概率为0.5
C.该物理量一次测量结果大于10.01的概率与小于9.99的概率相等
D.该物理量一次测量结果落在
D
[解析]
由正态密度曲线的对称性可知该物理量一次测量大于10的概率为0.5,故B正确;
由正态密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等,故C正确;
因为该物理量一次测量结果落在
方法总结 正态曲线的应用及求解策略:解答此类题目的关键在于将待求的问题向
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿(
在达尔文发表了《物种起源》之后,高尔顿也将研究方向转向生物及遗传学,他第一个对同卵双胞胎进行研究,论证了指纹的永久性和独特性.他从遗传的观点研究人类智力并提出“优生学”,是第一个强调把统计学方法应用到生物学中去的人.
拓展延伸·育素养
LONGCHENG NO.1 MIDDLE SCHOOL
二、高尔顿板
高尔顿设计了一个钉板实验,希望用统计的观点来解释遗传现象.
如图所示,木板上钉了数排(
小球在下落的过程中碰到任何钉子后,都将以
让一个个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小钉子碰撞,最后掉入高尔顿板下方的某一球槽内,如果球的数目相当大,它们在底板将组成近似中间高两头低,呈左右对称的图形.上面的钉板试验可绘制成如图所示的曲线,这就是我们学习过的正态曲线.
试验表明,只要小球足够多,它们在底板堆成的形状将近似于正态分布.
三、以高尔顿板为背景的题目
由高尔顿板衍生出的题目很多,下面举一例,供赏析.
案例 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与
层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图1所示的高尔顿板有7层小木块,小球从通道口落下,第一次与第2层中间的小木块碰撞,以
(1)如图1,进行一次高尔顿板试验,求小球掉入5号球槽的概率.
(2)小红和小明在研究了高尔顿板后,利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板,付费6元可以玩一次游戏,小球掉入
[解析] (1)设“这个小球掉入5号球槽”为事件
所以这个小球掉入5号球槽的概率为
(2)小红的收益计算如下:每一次游戏中,
则
所以
一次游戏付出的奖金
小明的收益计算如下:每一次游戏中,
则
所以
一次游戏付出的奖金
显然,
点评 本题以高尔顿板为背景,考查独立重复试验的概率问题以及离散型随机变量的分布列和数学期望,渗透了数学文化,意在考查考生的数据分析、数学运算以及逻辑推理的素养.解题关键是根据具体情况确定
第七章 随机变量及其分布
第七章章末小结
知识导图·明架构
题型探究·悟思路
拓展延伸·育素养
知识导图·明架构
LONGCHENG NO.1 MIDDLE SCHOOL
题型1 条件概率
例1 在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
方法指导 本题是条件概率问题,根据条件概率公式求解即可.
题型探究·悟思路
LONGCHENG NO.1 MIDDLE SCHOOL
[解析] 设“第1次抽到理科题”为事件
(1)从5道题中不放回地依次抽取2道题的事件数为
根据分步乘法计数原理,
于是
(2)因为
(3)(法一)由(1)(2)可得,在第1次抽到理科题的条件下,第2次抽到理科题的概率
(法二)因为
方法总结 求条件概率的主要方法有:(1)利用条件概率公式
题型2 乘法公式与全概率公式
例2 已知甲袋中有3个白球,2个黑球;乙袋中有4个白球,4个黑球.现从甲袋中任取2个球放入乙袋,然后再从乙袋中任取一球,求此球为白球的概率.
[解析] 记事件
记事件
则
由全概率公式可得
方法总结 本题考查利用全概率公式计算事件的概率,解题的关键在于确定从甲袋取出的2个球中白球的个数,结合全概率公式进行计算,本题渗透了数据分析以及数学运算的素养.
题型3 超几何分布
例3 随着互联网金融的发展,很多平台都推出了自己的虚拟信用支付,比较常用的有蚂蚁花呗、京东白条.花呗与信用卡有一个共同点就是可以透支消费,对于很多90后来说,他们更习惯提前消费.某研究机构随机抽取了1000名90后,对他们的信用支付方式进行了调查,得到如下统计表:
信用支付方式 银行信用卡 蚂蚁花呗 京东白条 其他
人数 300
每个人都仅使用一种信用支付方式,各人支付方式相互独立,以频率估计概率.
(1)估计90后使用蚂蚁花呗的概率;
(2)在所抽取的1000人中用分层随机抽样的方法,先在使用银行信用卡和蚂蚁花呗的人中随机抽取8人,再在这8人中随机抽取4人,记
[解析] (1)
(2)这8人中使用信用卡的人数为
故随机变量
所以
所以随机变量
故
方法总结 超几何分布的求解步骤:(1)辨模型:结合实际情景分析所求概率分布问题是否具有明显的两部分组成,如“男生、女生”“正品、次品”“优、劣”等.(2)算概率:可以直接借助公式
题型4 独立事件
例4 [2021年新高考全国Ⅰ卷] 有6个相同的球,分别标有数字
A.甲与丙相互独立 B.甲与丁相互独立 C.乙与丙相互独立 D.丙与丁相互独立
B
[解析] 由题意得,
则
方法总结 求相互独立事件,一般与互斥事件、对立事件结合在一起进行考查,解答此类问题时应分清事件间的内部联系,在此基础上用基本事件之间的交、并、补运算表示出有关事件,并运用相应公式求解.解题过程渗透了数学运算、逻辑推理的素养.
题型5 二项分布
例5 [2021年天津卷] 甲、乙两人在每次猜谜活动中各猜一个谜语,若一方猜对且另一方猜错,则猜对的一方获胜,否则本次平局.已知每次活动中,甲、乙猜对的概率分别为
[解析] 由题意可得,1次活动中,甲获胜的概率为
则在3次活动中,甲至少获胜2次的概率为
方法总结 解决二项分布问题的两个关注点:(1)对于公式
题型6 离散型随机变量的均值与方差
例6 [2021年新高考全国Ⅰ卷] 某学校组织“一带一路”知识竞赛,有
(1)若小明先回答
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
[解析] (1)由题意可知,
则
所以
(2)由(1)知,小明先回答
若小明先回答
则
所以
因为
方法总结 求离散型随机变量的均值、方差的步骤:
题型7 正态分布
例7 某物理量的测量结果服从正态分布
A.
B.该物理量一次测量结果大于10的概率为0.5
C.该物理量一次测量结果大于10.01的概率与小于9.99的概率相等
D.该物理量一次测量结果落在
D
[解析]
由正态密度曲线的对称性可知该物理量一次测量大于10的概率为0.5,故B正确;
由正态密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等,故C正确;
因为该物理量一次测量结果落在
方法总结 正态曲线的应用及求解策略:解答此类题目的关键在于将待求的问题向
高尔顿与高尔顿板
一、高尔顿简介
弗朗西斯·高尔顿(
在达尔文发表了《物种起源》之后,高尔顿也将研究方向转向生物及遗传学,他第一个对同卵双胞胎进行研究,论证了指纹的永久性和独特性.他从遗传的观点研究人类智力并提出“优生学”,是第一个强调把统计学方法应用到生物学中去的人.
拓展延伸·育素养
LONGCHENG NO.1 MIDDLE SCHOOL
二、高尔顿板
高尔顿设计了一个钉板实验,希望用统计的观点来解释遗传现象.
如图所示,木板上钉了数排(
小球在下落的过程中碰到任何钉子后,都将以
让一个个小球从高尔顿板上方的通道口落下,小球在下落过程中与层层小钉子碰撞,最后掉入高尔顿板下方的某一球槽内,如果球的数目相当大,它们在底板将组成近似中间高两头低,呈左右对称的图形.上面的钉板试验可绘制成如图所示的曲线,这就是我们学习过的正态曲线.
试验表明,只要小球足够多,它们在底板堆成的形状将近似于正态分布.
三、以高尔顿板为背景的题目
由高尔顿板衍生出的题目很多,下面举一例,供赏析.
案例 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与
层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图1所示的高尔顿板有7层小木块,小球从通道口落下,第一次与第2层中间的小木块碰撞,以
(1)如图1,进行一次高尔顿板试验,求小球掉入5号球槽的概率.
(2)小红和小明在研究了高尔顿板后,利用高尔顿板来到社团文化节上进行盈利性“抽奖”活动.小红使用图1所示的高尔顿板,付费6元可以玩一次游戏,小球掉入
[解析] (1)设“这个小球掉入5号球槽”为事件
所以这个小球掉入5号球槽的概率为
(2)小红的收益计算如下:每一次游戏中,
则
所以
一次游戏付出的奖金
小明的收益计算如下:每一次游戏中,
则
所以
一次游戏付出的奖金
显然,
点评 本题以高尔顿板为背景,考查独立重复试验的概率问题以及离散型随机变量的分布列和数学期望,渗透了数学文化,意在考查考生的数据分析、数学运算以及逻辑推理的素养.解题关键是根据具体情况确定
