高一下学期物理人教版(2019)必修第二册8.4机械能守恒定律(功能关系) 课件 (共13张PPT)
文档属性
| 名称 | 高一下学期物理人教版(2019)必修第二册8.4机械能守恒定律(功能关系) 课件 (共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-07 21:38:22 | ||
图片预览




文档简介
(共13张PPT)
§8.43 机械能守恒定律
(功能关系、能量守恒)
第八章 机械能守恒定律
课前练. 3.(多选)如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,物体A置于光滑水平桌面上,A右端连接一根细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让A处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是( )
A.A物体与B物体组成的系统机械能守恒
B.A物体与B物体组成的系统机械能不守恒
C.B物体机械能的减少量小于弹簧弹性势能的增加量
D.当弹簧的拉力等于B物体的重力时,A物体的动能最大
BD
系统集成 第127页
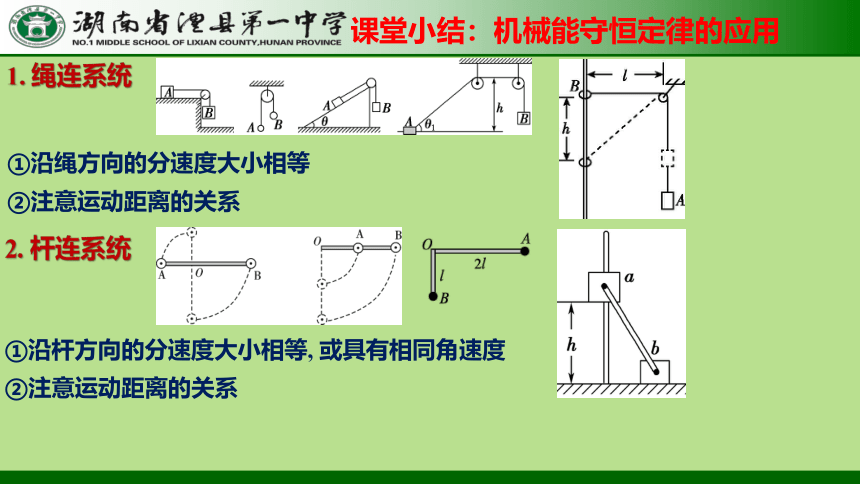
课堂小结:机械能守恒定律的应用
1. 绳连系统
①沿绳方向的分速度大小相等
②注意运动距离的关系
2. 杆连系统
①沿杆方向的分速度大小相等, 或具有相同角速度
②注意运动距离的关系
[拓展] 如图所示,位于竖直平面内的光滑轨道,由一段斜面轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的物块从斜面轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.
2.5R≤h≤5R
系统集成 第125页
[拓展] 如图所示,位于竖直平面内的光滑轨道,由一段斜面轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的物块从斜面轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.
2.5R≤h≤5R
系统集成 第125页
解 ① 恰通过最高点时: mg =
由动能定理 mg(h1-2R)=mv12
得 h1=2.5R
② 最高点压力为5mg时: 5mg+mg =
由动能定理 mg(h2-2R)=mv22
得 h2=5R
即 2.5R ≤ h ≤ 5R
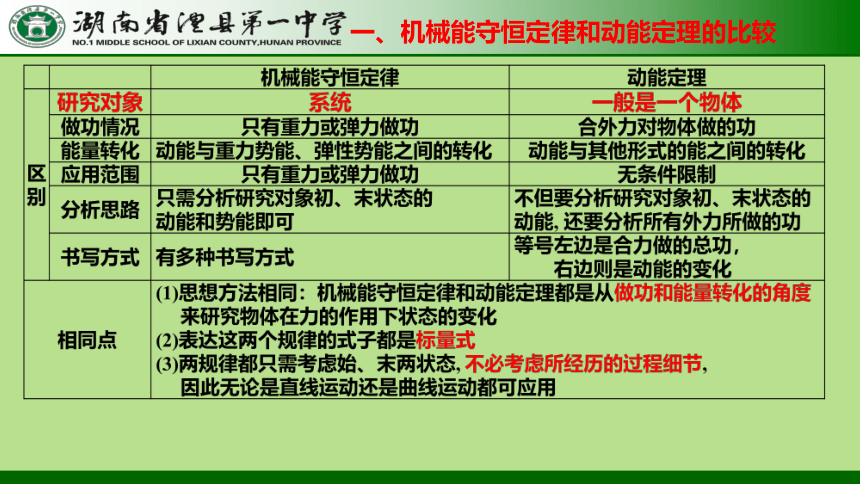
一、机械能守恒定律和动能定理的比较
[例3] 如图所示,某段滑雪雪道倾角为30°,总质量为m(包括雪具在内)的滑雪运动员从距底端高为h处的雪道上由静止开始匀加速下滑,加速度为g.在他从上向下滑到底端的过程中,下列说法正确的是( )
A.运动员减少的重力势能全部转化为动能
B.运动员获得的动能为mgh
C.运动员克服摩擦力做的功为mgh
D.下滑过程中系统减少的机械能为mgh
课堂探究一:
(1)机械能不守恒时, 如何计算机械能的变化量
(2)试从功能关系推导机械能的变化与什么力做功有关
D
系统集成 第126页
W其它=ΔE机
二、功能关系
二、功能关系
2.质量为m的物体,由静止开始下落,由于阻力作用,下落的加速度为g,在物体下落h的过程中,下列说法不正确的是( )
A.物体的动能增加了mgh
B.物体的重力势能减少了mgh
C.物体的机械能减少了mgh
D.物体克服阻力所做的功为mgh
C
系统集成 第127页
[针对训练2] 如图所示,AB和CD为两个对称斜面,其上部足够长,下部分别与一个光滑的圆弧面的两端相切,圆弧圆心角为120°,半径R=2.0 m,一个质量m=1 kg的物体(可看成质点)在离圆弧底端高度为h=3.0 m处,以4.0 m/s的初速度沿斜面向下运动,若物体与斜面间的动摩擦因数μ=0.2,重力加速度g=10 m/s2,则:
(1)试描述物体最终的运动情况.
(2)物体在斜面上(不包括圆弧部分)
走过路程的最大值为多少?
(3)物体对圆弧轨道最低点的最大压力和
最小压力分别为多少?(结果中可以保留根号)
系统集成 第126页
课堂小结:功能关系
一、机械能守恒定律和动能定理的比较
二、功能关系
1.如图所示,质量分别为m和3m的小球A和B,系在长为L的细线两端,桌面水平光滑,离地高度为h(hA
系统集成 第127页
§8.43 机械能守恒定律
(功能关系、能量守恒)
第八章 机械能守恒定律
课前练. 3.(多选)如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,物体A置于光滑水平桌面上,A右端连接一根细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让A处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是( )
A.A物体与B物体组成的系统机械能守恒
B.A物体与B物体组成的系统机械能不守恒
C.B物体机械能的减少量小于弹簧弹性势能的增加量
D.当弹簧的拉力等于B物体的重力时,A物体的动能最大
BD
系统集成 第127页
课堂小结:机械能守恒定律的应用
1. 绳连系统
①沿绳方向的分速度大小相等
②注意运动距离的关系
2. 杆连系统
①沿杆方向的分速度大小相等, 或具有相同角速度
②注意运动距离的关系
[拓展] 如图所示,位于竖直平面内的光滑轨道,由一段斜面轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的物块从斜面轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.
2.5R≤h≤5R
系统集成 第125页
[拓展] 如图所示,位于竖直平面内的光滑轨道,由一段斜面轨道和与之相切的圆形轨道连接而成,圆形轨道的半径为R.一质量为m的物块从斜面轨道上某处由静止开始下滑,然后沿圆形轨道运动.要求物块能通过圆形轨道最高点,且在该最高点与轨道间的压力不能超过5mg(g为重力加速度).求物块初始位置相对于圆形轨道底部的高度h的取值范围.
2.5R≤h≤5R
系统集成 第125页
解 ① 恰通过最高点时: mg =
由动能定理 mg(h1-2R)=mv12
得 h1=2.5R
② 最高点压力为5mg时: 5mg+mg =
由动能定理 mg(h2-2R)=mv22
得 h2=5R
即 2.5R ≤ h ≤ 5R
一、机械能守恒定律和动能定理的比较
[例3] 如图所示,某段滑雪雪道倾角为30°,总质量为m(包括雪具在内)的滑雪运动员从距底端高为h处的雪道上由静止开始匀加速下滑,加速度为g.在他从上向下滑到底端的过程中,下列说法正确的是( )
A.运动员减少的重力势能全部转化为动能
B.运动员获得的动能为mgh
C.运动员克服摩擦力做的功为mgh
D.下滑过程中系统减少的机械能为mgh
课堂探究一:
(1)机械能不守恒时, 如何计算机械能的变化量
(2)试从功能关系推导机械能的变化与什么力做功有关
D
系统集成 第126页
W其它=ΔE机
二、功能关系
二、功能关系
2.质量为m的物体,由静止开始下落,由于阻力作用,下落的加速度为g,在物体下落h的过程中,下列说法不正确的是( )
A.物体的动能增加了mgh
B.物体的重力势能减少了mgh
C.物体的机械能减少了mgh
D.物体克服阻力所做的功为mgh
C
系统集成 第127页
[针对训练2] 如图所示,AB和CD为两个对称斜面,其上部足够长,下部分别与一个光滑的圆弧面的两端相切,圆弧圆心角为120°,半径R=2.0 m,一个质量m=1 kg的物体(可看成质点)在离圆弧底端高度为h=3.0 m处,以4.0 m/s的初速度沿斜面向下运动,若物体与斜面间的动摩擦因数μ=0.2,重力加速度g=10 m/s2,则:
(1)试描述物体最终的运动情况.
(2)物体在斜面上(不包括圆弧部分)
走过路程的最大值为多少?
(3)物体对圆弧轨道最低点的最大压力和
最小压力分别为多少?(结果中可以保留根号)
系统集成 第126页
课堂小结:功能关系
一、机械能守恒定律和动能定理的比较
二、功能关系
1.如图所示,质量分别为m和3m的小球A和B,系在长为L的细线两端,桌面水平光滑,离地高度为h(h
系统集成 第127页
