高一下学期物理人教版(2019)必修第二册 8.4机械能守恒定律(系统机械能守恒) 课件 (共14张PPT)
文档属性
| 名称 | 高一下学期物理人教版(2019)必修第二册 8.4机械能守恒定律(系统机械能守恒) 课件 (共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-07 21:41:36 | ||
图片预览



文档简介
(共14张PPT)
§8.42 机械能守恒定律
(系统机械能守恒)
第八章 机械能守恒定律
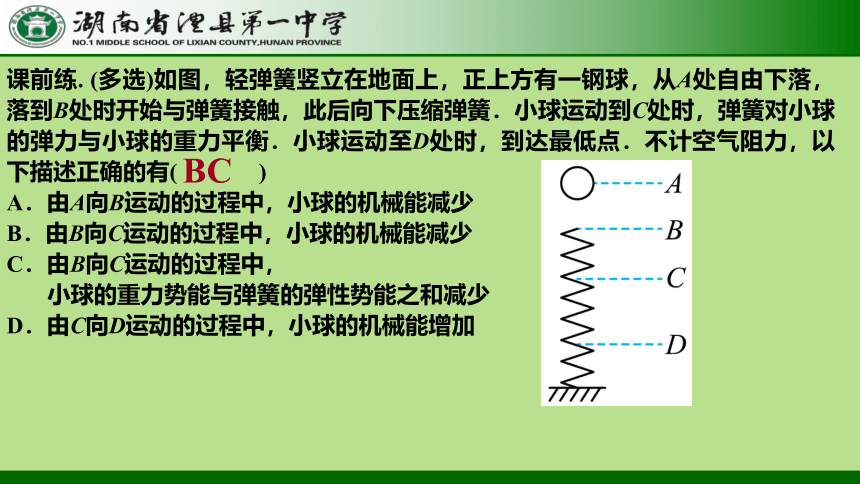
课前练. (多选)如图,轻弹簧竖立在地面上,正上方有一钢球,从A处自由下落,落到B处时开始与弹簧接触,此后向下压缩弹簧.小球运动到C处时,弹簧对小球的弹力与小球的重力平衡.小球运动至D处时,到达最低点.不计空气阻力,以下描述正确的有( )
A.由A向B运动的过程中,小球的机械能减少
B.由B向C运动的过程中,小球的机械能减少
C.由B向C运动的过程中,
小球的重力势能与弹簧的弹性势能之和减少
D.由C向D运动的过程中,小球的机械能增加
BC
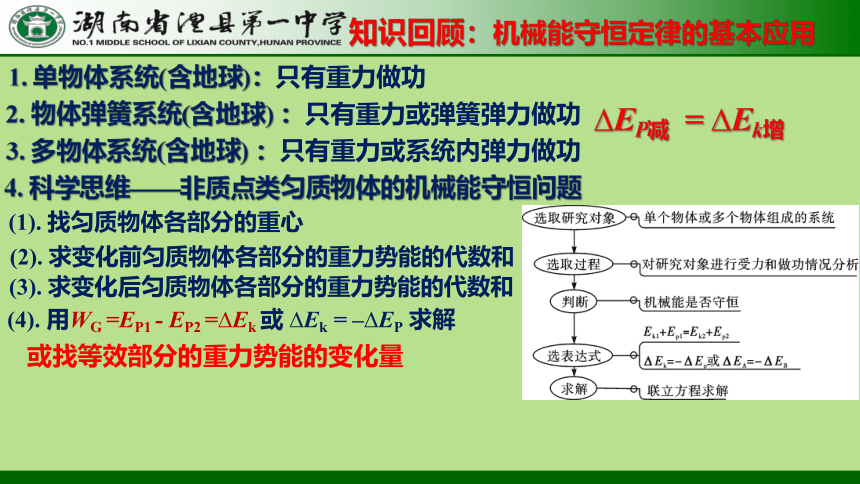
1. 单物体系统(含地球):只有重力做功
2. 物体弹簧系统(含地球) :只有重力或弹簧弹力做功
3. 多物体系统(含地球) :只有重力或系统内弹力做功
4. 科学思维——非质点类匀质物体的机械能守恒问题
(2). 求变化前匀质物体各部分的重力势能的代数和
(4). 用WG =EP1 - EP2 = Ek 或 Ek = – EP 求解
(3). 求变化后匀质物体各部分的重力势能的代数和
(1). 找匀质物体各部分的重心
或找等效部分的重力势能的变化量
EP减 = Ek增
知识回顾:机械能守恒定律的基本应用
[例3] 如图所示,两小球A、B系在跨过定滑轮的细绳两端, 小球A的质量mA=2 kg, 小球B的质量mB=1 kg, 最初用手将A、B托住处于静止, 绳上恰好没有张力, 此时A比B高h=1.2 m.将A、B同时释放, g取10 m/s2, 求:
(1)释放前, 以B所在位置的水平面为参考平面, A的重力势能;
(2)释放后, 当A、B到达同一高度时, A、B的速度大小.
(1)24 J (2)2 m/s
系统集成 第121页
[例3] 如图所示,两小球A、B系在跨过定滑轮的细绳两端, 小球A的质量mA=2 kg, 小球B的质量mB=1 kg, 最初用手将A、B托住处于静止, 绳上恰好没有张力, 此时A比B高h=1.2 m.将A、B同时释放, g取10 m/s2, 求:
(1)释放前, 以B所在位置的水平面为参考平面, A的重力势能;
(2)释放后, 当A、B到达同一高度时, A、B的速度大小.
系统集成 第121页
解 (2)对AB, 该过程由机械能守恒定律:
mA g ─ mB g =mAv2 + mBv2
得 v=2 m/s
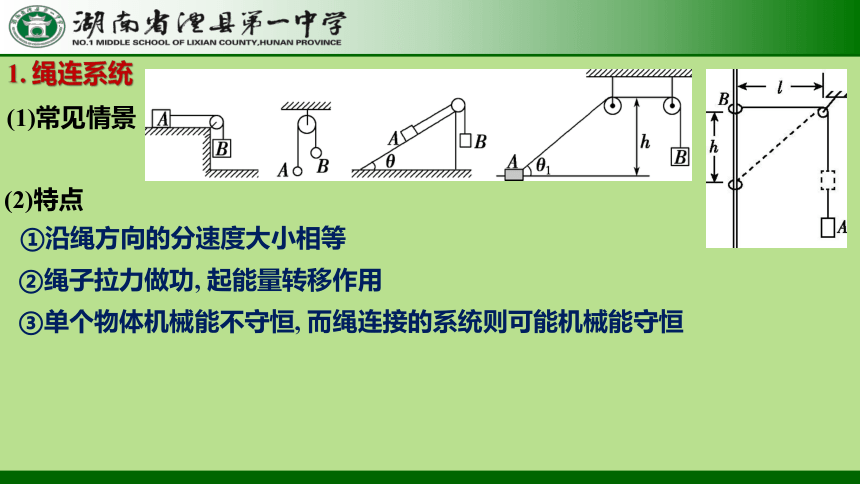
1. 绳连系统
(1)常见情景
①沿绳方向的分速度大小相等
(2)特点
②绳子拉力做功, 起能量转移作用
③单个物体机械能不守恒, 而绳连接的系统则可能机械能守恒
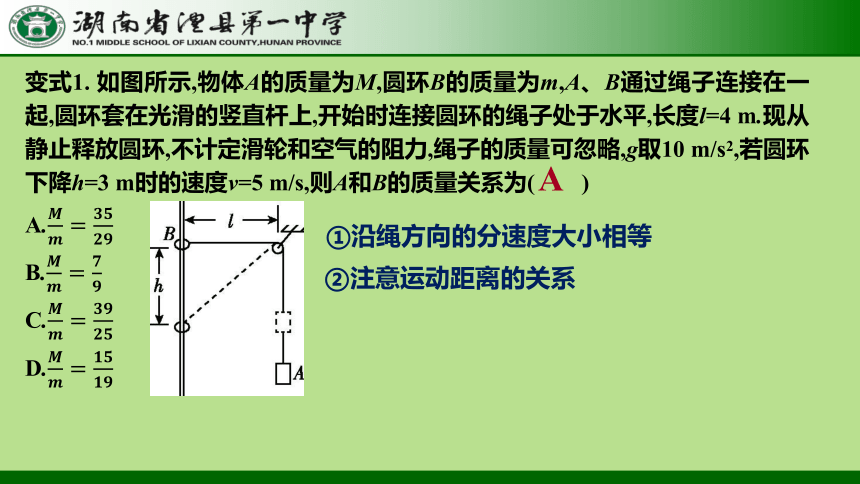
变式1. 如图所示,物体A的质量为M,圆环B的质量为m,A、B通过绳子连接在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,长度l=4 m.现从静止释放圆环,不计定滑轮和空气的阻力,绳子的质量可忽略,g取10 m/s2,若圆环下降h=3 m时的速度v=5 m/s,则A和B的质量关系为( )
A.
B.
C.
D.
A
①沿绳方向的分速度大小相等
②注意运动距离的关系
[例1] 如图所示,A、B两小球分别固定在一刚性轻杆的两端,两球球心间相距L=1.0 m,两球质量分别为mA=4.0 kg, mB=1.0 kg,杆上距A球球心0.40 m处有一水平轴O,杆可绕轴无摩擦转动,现先使杆保持水平,然后从静止释放.当杆转到竖直位置,则:(重力加速度g取10 m/s2)
(1)两球的速度大小各是多少?
(2)转动过程中杆对A球做的功为多少?
系统集成 第124页
2. 杆连系统
(1)常见情景
①沿杆方向的分速度大小相等, 或具有相同角速度
(2)特点
②杆中弹力做功, 起能量转移作用
③单个物体机械能不守恒, 而杆连接的系统则可能机械能守恒
变式2. 如图所示,在长为的轻杆中点A和端点B各固定一质量为的小球,杆可绕轴在竖直面内转动(无摩擦),不计空气阻力,将杆拉至水平位置后无初速度释放.根据圆周运动的特点,转动过程中任意时刻B球的速度大小均是A球的两倍,重力加速度大小为g,则当杆转到竖直位置时,求:
(1)A球的速度
(2)该过程轻杆对A球做的功
;
变式2. 如图所示,在长为的轻杆中点A和端点B各固定一质量为的小球,杆可绕轴在竖直面内转动(无摩擦),不计空气阻力,将杆拉至水平位置后无初速度释放.根据圆周运动的特点,转动过程中任意时刻B球的速度大小均是A球的两倍,重力加速度大小为g,则当杆转到竖直位置时,求:
(1)A球的速度
(2)该过程轻杆对A球做的功WA
解 (1)对AB, 该过程, 由机械能守恒定律:
mg + mgL=mvA2 + mvB2
得 vA=
(2)对A, 由动能定理:
mg + WA=mvA2
得 WA=-0.2mgL
课堂小结:机械能守恒定律的应用
1. 绳连系统
①沿绳方向的分速度大小相等
②注意运动距离的关系
2. 杆连系统
①沿杆方向的分速度大小相等, 或具有相同角速度
②注意运动距离的关系
[针对训练1] 如图所示,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上半径为R的光滑圆柱,A的质量为B的两倍.当B位于地面时,A恰好与圆柱轴心等高.将A由静止释放,B上升的最大高度是( )
A.2R
B.
C.
D.
C
系统集成 第124页
变式3. 如图,两质量相等可视为质点的小球 A、B,用一根长为 0.2m 的轻杆相连,开始时两小球置于光滑水平面上,给两小球一个 2m/s 水平向左的初速度,经一段时间,两小球滑上倾角为 30°的足够长光滑斜面,不计球与斜面碰撞时的机械能损失,g 取 10m/s2,在两小球的速度减小为零的过称中,下列说法正确的是( )
A.轻杆对小球 A 做负功
B.轻杆对小球 B 做正功
C.运动过程中,小球 A、B 的速度大小始终相等
D.小球 B 距水平面的最大高度为 0.15m
D
§8.42 机械能守恒定律
(系统机械能守恒)
第八章 机械能守恒定律
课前练. (多选)如图,轻弹簧竖立在地面上,正上方有一钢球,从A处自由下落,落到B处时开始与弹簧接触,此后向下压缩弹簧.小球运动到C处时,弹簧对小球的弹力与小球的重力平衡.小球运动至D处时,到达最低点.不计空气阻力,以下描述正确的有( )
A.由A向B运动的过程中,小球的机械能减少
B.由B向C运动的过程中,小球的机械能减少
C.由B向C运动的过程中,
小球的重力势能与弹簧的弹性势能之和减少
D.由C向D运动的过程中,小球的机械能增加
BC
1. 单物体系统(含地球):只有重力做功
2. 物体弹簧系统(含地球) :只有重力或弹簧弹力做功
3. 多物体系统(含地球) :只有重力或系统内弹力做功
4. 科学思维——非质点类匀质物体的机械能守恒问题
(2). 求变化前匀质物体各部分的重力势能的代数和
(4). 用WG =EP1 - EP2 = Ek 或 Ek = – EP 求解
(3). 求变化后匀质物体各部分的重力势能的代数和
(1). 找匀质物体各部分的重心
或找等效部分的重力势能的变化量
EP减 = Ek增
知识回顾:机械能守恒定律的基本应用
[例3] 如图所示,两小球A、B系在跨过定滑轮的细绳两端, 小球A的质量mA=2 kg, 小球B的质量mB=1 kg, 最初用手将A、B托住处于静止, 绳上恰好没有张力, 此时A比B高h=1.2 m.将A、B同时释放, g取10 m/s2, 求:
(1)释放前, 以B所在位置的水平面为参考平面, A的重力势能;
(2)释放后, 当A、B到达同一高度时, A、B的速度大小.
(1)24 J (2)2 m/s
系统集成 第121页
[例3] 如图所示,两小球A、B系在跨过定滑轮的细绳两端, 小球A的质量mA=2 kg, 小球B的质量mB=1 kg, 最初用手将A、B托住处于静止, 绳上恰好没有张力, 此时A比B高h=1.2 m.将A、B同时释放, g取10 m/s2, 求:
(1)释放前, 以B所在位置的水平面为参考平面, A的重力势能;
(2)释放后, 当A、B到达同一高度时, A、B的速度大小.
系统集成 第121页
解 (2)对AB, 该过程由机械能守恒定律:
mA g ─ mB g =mAv2 + mBv2
得 v=2 m/s
1. 绳连系统
(1)常见情景
①沿绳方向的分速度大小相等
(2)特点
②绳子拉力做功, 起能量转移作用
③单个物体机械能不守恒, 而绳连接的系统则可能机械能守恒
变式1. 如图所示,物体A的质量为M,圆环B的质量为m,A、B通过绳子连接在一起,圆环套在光滑的竖直杆上,开始时连接圆环的绳子处于水平,长度l=4 m.现从静止释放圆环,不计定滑轮和空气的阻力,绳子的质量可忽略,g取10 m/s2,若圆环下降h=3 m时的速度v=5 m/s,则A和B的质量关系为( )
A.
B.
C.
D.
A
①沿绳方向的分速度大小相等
②注意运动距离的关系
[例1] 如图所示,A、B两小球分别固定在一刚性轻杆的两端,两球球心间相距L=1.0 m,两球质量分别为mA=4.0 kg, mB=1.0 kg,杆上距A球球心0.40 m处有一水平轴O,杆可绕轴无摩擦转动,现先使杆保持水平,然后从静止释放.当杆转到竖直位置,则:(重力加速度g取10 m/s2)
(1)两球的速度大小各是多少?
(2)转动过程中杆对A球做的功为多少?
系统集成 第124页
2. 杆连系统
(1)常见情景
①沿杆方向的分速度大小相等, 或具有相同角速度
(2)特点
②杆中弹力做功, 起能量转移作用
③单个物体机械能不守恒, 而杆连接的系统则可能机械能守恒
变式2. 如图所示,在长为的轻杆中点A和端点B各固定一质量为的小球,杆可绕轴在竖直面内转动(无摩擦),不计空气阻力,将杆拉至水平位置后无初速度释放.根据圆周运动的特点,转动过程中任意时刻B球的速度大小均是A球的两倍,重力加速度大小为g,则当杆转到竖直位置时,求:
(1)A球的速度
(2)该过程轻杆对A球做的功
;
变式2. 如图所示,在长为的轻杆中点A和端点B各固定一质量为的小球,杆可绕轴在竖直面内转动(无摩擦),不计空气阻力,将杆拉至水平位置后无初速度释放.根据圆周运动的特点,转动过程中任意时刻B球的速度大小均是A球的两倍,重力加速度大小为g,则当杆转到竖直位置时,求:
(1)A球的速度
(2)该过程轻杆对A球做的功WA
解 (1)对AB, 该过程, 由机械能守恒定律:
mg + mgL=mvA2 + mvB2
得 vA=
(2)对A, 由动能定理:
mg + WA=mvA2
得 WA=-0.2mgL
课堂小结:机械能守恒定律的应用
1. 绳连系统
①沿绳方向的分速度大小相等
②注意运动距离的关系
2. 杆连系统
①沿杆方向的分速度大小相等, 或具有相同角速度
②注意运动距离的关系
[针对训练1] 如图所示,可视为质点的小球A、B用不可伸长的细软轻线连接,跨过固定在地面上半径为R的光滑圆柱,A的质量为B的两倍.当B位于地面时,A恰好与圆柱轴心等高.将A由静止释放,B上升的最大高度是( )
A.2R
B.
C.
D.
C
系统集成 第124页
变式3. 如图,两质量相等可视为质点的小球 A、B,用一根长为 0.2m 的轻杆相连,开始时两小球置于光滑水平面上,给两小球一个 2m/s 水平向左的初速度,经一段时间,两小球滑上倾角为 30°的足够长光滑斜面,不计球与斜面碰撞时的机械能损失,g 取 10m/s2,在两小球的速度减小为零的过称中,下列说法正确的是( )
A.轻杆对小球 A 做负功
B.轻杆对小球 B 做正功
C.运动过程中,小球 A、B 的速度大小始终相等
D.小球 B 距水平面的最大高度为 0.15m
D
