生活中的轴对称[下学期]
图片预览

文档简介
第五章 生活中的轴对称
一、基础知识梳理
(一)主要概念
1.轴对称图形:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
角是轴对称图形,角平分线所在的直线是它的对称轴.
2.线段的垂直平分线:线段是轴对称图形,它的一条对称轴垂直于这条线段并且平分它,这样的直线叫做这条线段的垂直平分线(简称中垂线).
3.等腰三角形:有两条边相等的三角形叫做等腰三角形.
(二)主要性质
1.角的平分线上的点到这个角的两边的距离相等.
2.线段垂直平分线上的点到这条线段两个端点的距离相等.
3.等腰三角形是轴对称图形
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.等腰三角形的两个底角相等.
4.两个图形关于某条直线成轴对称,则对应点所连的线段被对称轴垂直平分.
对应线段相等,对就角相等.
二、考点与命题趋向分析
(一)能力
1.通过具体实例认识轴对称,探索它的基本性质,理解对应点所连的线段被对称轴垂直平分的性质.
2.能够按要求作出简单平面图形经过一次或两次轴对称后的图形;探索简单图形之间的轴对称关系,并能指出对称轴.
3.探索基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称性及其相关性质.
4.欣赏现实生活中的轴对称图形,结合现实生活中典型实例了解并欣赏物体的镜面对称,能利用轴对称进行图案设计.
5.了解角平分线及其性质.
6.了解线段垂直平分线及其性质.
7.了解等腰三角形的有关概念,探索并掌握等腰三角形的性质.
(二)命题趋向分析
1.中考中常在拼图中考查轴对称的有关概念,考查学生动手操作能力.
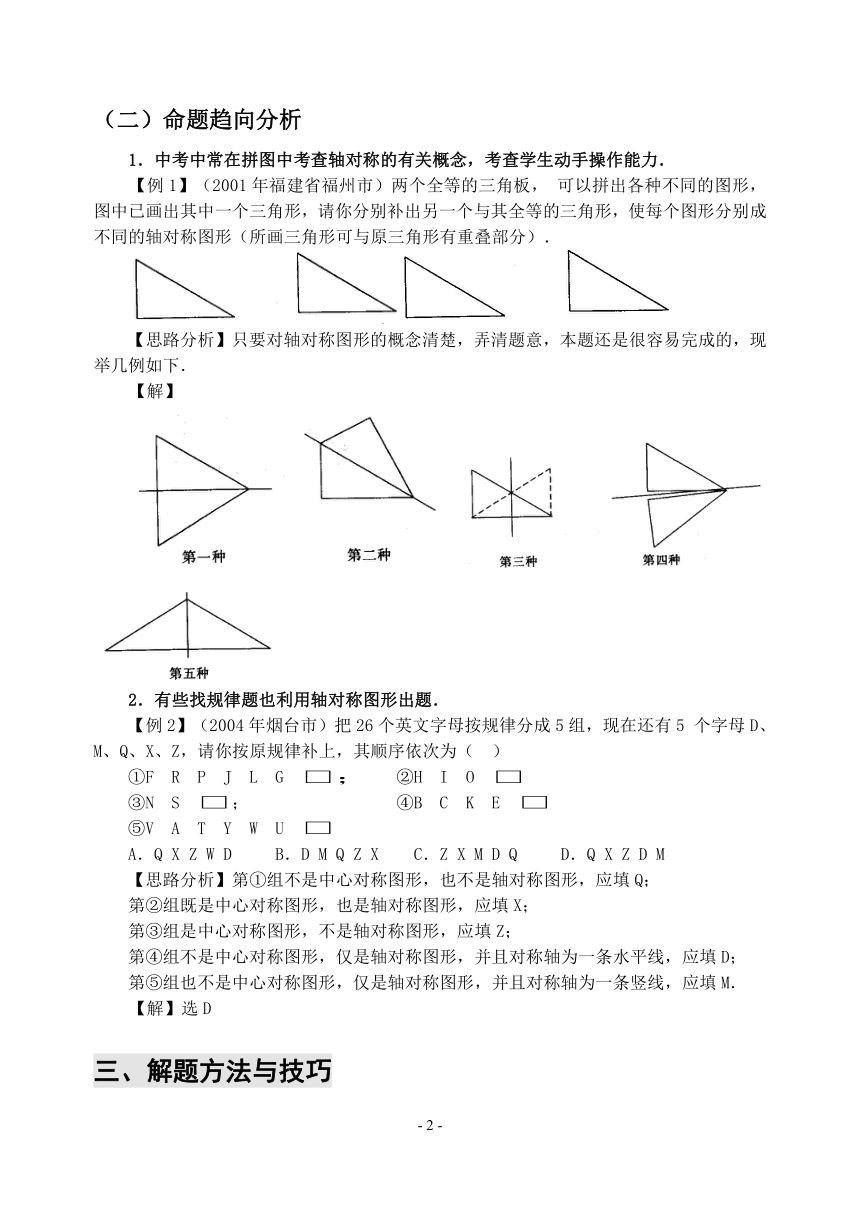
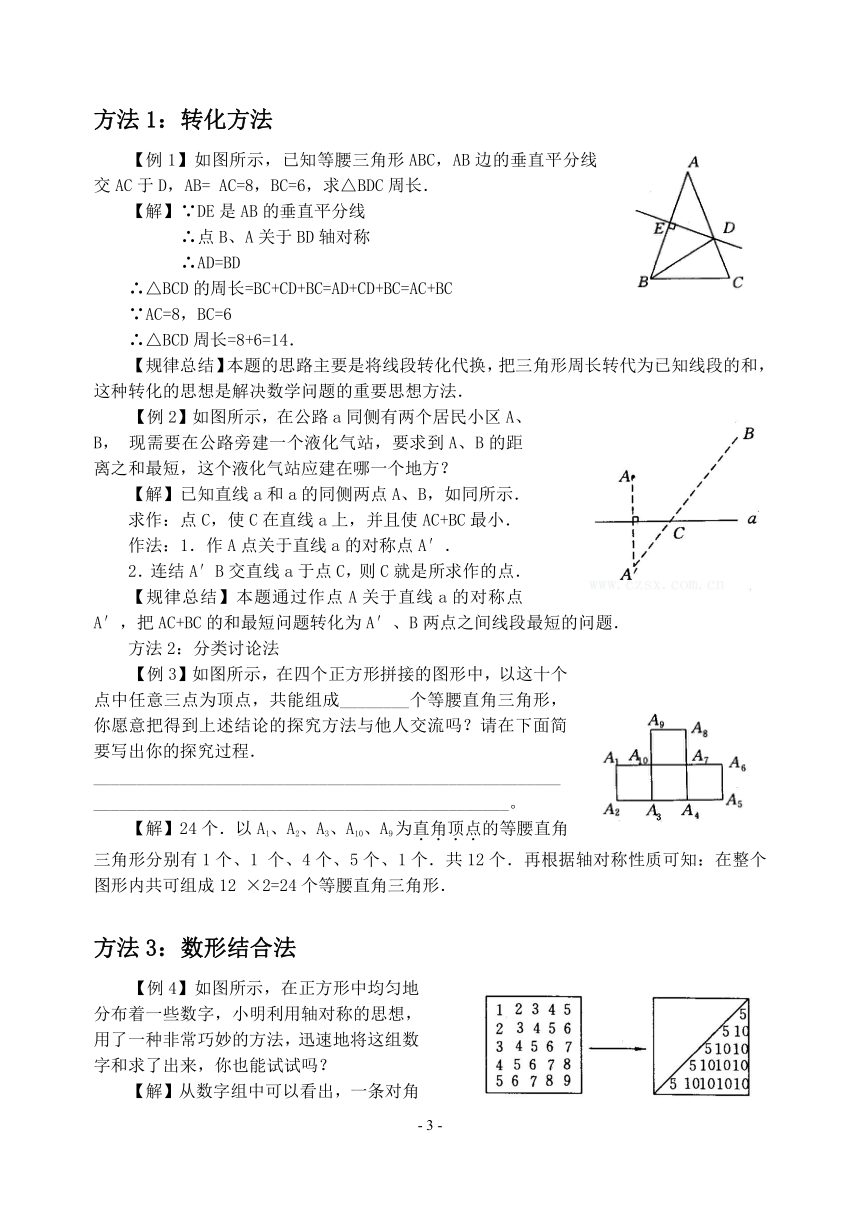
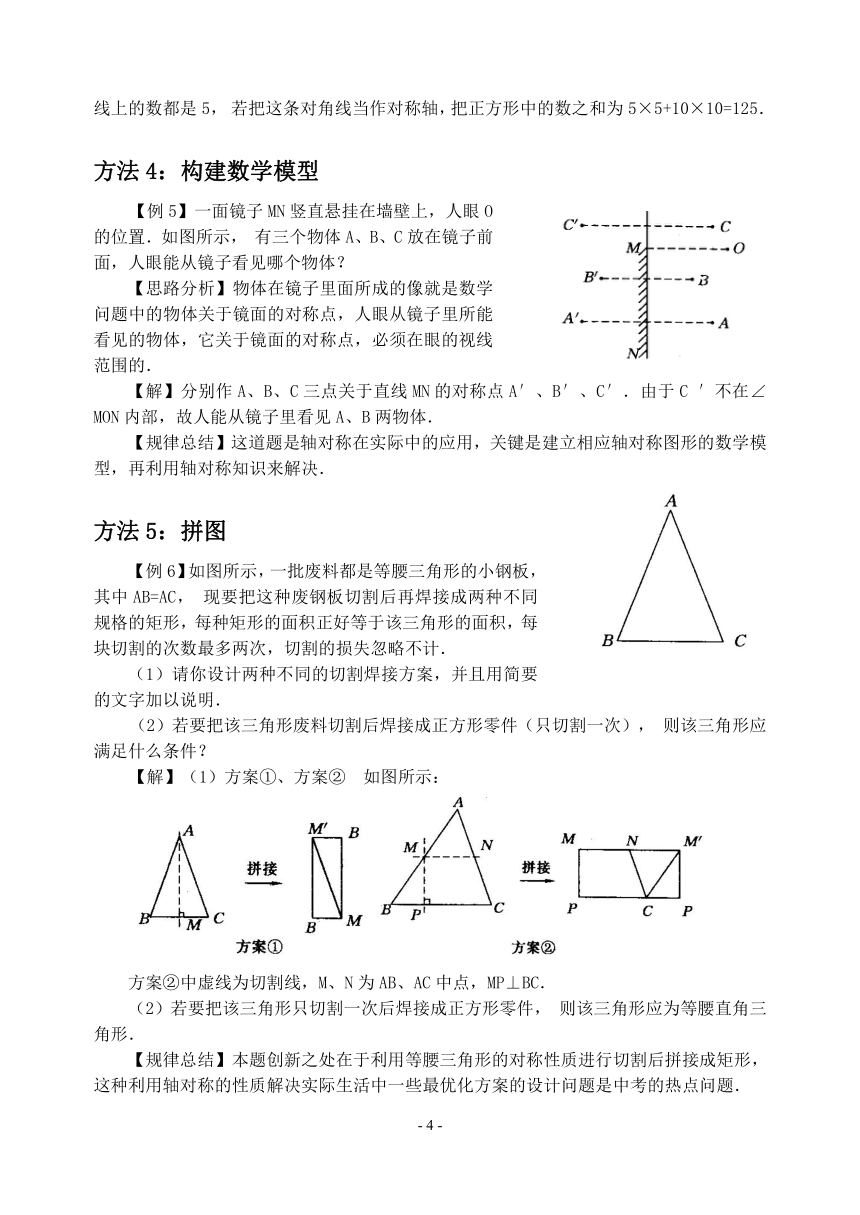
【例1】(2001年福建省福州市)两个全等的三角板,可以拼出各种不同的图形,图中已画出其中一个三角形,请你分别补出另一个与其全等的三角形,使每个图形分别成不同的轴对称图形(所画三角形可与原三角形有重叠部分).
【思路分析】只要对轴对称图形的概念清楚,弄清题意,本题还是很容易完成的,现举几例如下.
【解】
2.有些找规律题也利用轴对称图形出题.
【例2】(2004年烟台市)把26个英文字母按规律分成5组,现在还有5个字母D、M、Q、X、Z,请你按原规律补上,其顺序依次为( )
①F R P J L G □; ②H I O □
③N S □; ④B C K E □
⑤V A T Y W U □
A.Q X Z W D B.D M Q Z X C.Z X M D Q D.Q X Z D M
【思路分析】第①组不是中心对称图形,也不是轴对称图形,应填Q;
第②组既是中心对称图形,也是轴对称图形,应填X;
第③组是中心对称图形,不是轴对称图形,应填Z;
第④组不是中心对称图形,仅是轴对称图形,并且对称轴为一条水平线,应填D;
第⑤组也不是中心对称图形,仅是轴对称图形,并且对称轴为一条竖线,应填M.
【解】选D
三、解题方法与技巧
方法1:转化方法
【例1】如图所示,已知等腰三角形ABC,AB边的垂直平分线交AC于D,AB=AC=8,BC=6,求△BDC周长.
【解】∵DE是AB的垂直平分线
∴点B、A关于BD轴对称
∴AD=BD
∴△BCD的周长=BC+CD+BC=AD+CD+BC=AC+BC
∵AC=8,BC=6
∴△BCD周长=8+6=14.
【规律总结】本题的思路主要是将线段转化代换,把三角形周长转代为已知线段的和,这种转化的思想是解决数学问题的重要思想方法.
【例2】如图所示,在公路a同侧有两个居民小区A、B,现需要在公路旁建一个液化气站,要求到A、B的距离之和最短,这个液化气站应建在哪一个地方?
【解】已知直线a和a的同侧两点A、B,如同所示.
求作:点C,使C在直线a上,并且使AC+BC最小.
作法:1.作A点关于直线a的对称点A′.
2.连结A′B交直线a于点C,则C就是所求作的点.
【规律总结】本题通过作点A关于直线a的对称点A′,把AC+BC的和最短问题转化为A′、B两点之间线段最短的问题.
方法2:分类讨论法
【例3】如图所示,在四个正方形拼接的图形中,以这十个点中任意三点为顶点,共能组成________个等腰直角三角形,你愿意把得到上述结论的探究方法与他人交流吗?请在下面简要写出你的探究过程.
______________________________________________________________________________________________________。
【解】24个.以A1、A2、A3、A10、A9为直角顶点的等腰直角三角形分别有1个、1个、4个、5个、1个.共12个.再根据轴对称性质可知:在整个图形内共可组成12×2=24个等腰直角三角形.
方法3:数形结合法
【例4】如图所示,在正方形中均匀地分布着一些数字,小明利用轴对称的思想,用了一种非常巧妙的方法,迅速地将这组数字和求了出来,你也能试试吗?
【解】从数字组中可以看出,一条对角线上的数都是5,若把这条对角线当作对称轴,把正方形中的数之和为5×5+10×10=125.
方法4:构建数学模型
【例5】一面镜子MN竖直悬挂在墙壁上,人眼O的位置.如图所示,有三个物体A、B、C放在镜子前面,人眼能从镜子看见哪个物体?
【思路分析】物体在镜子里面所成的像就是数学问题中的物体关于镜面的对称点,人眼从镜子里所能看见的物体,它关于镜面的对称点,必须在眼的视线范围的.
【解】分别作A、B、C三点关于直线MN的对称点A′、B′、C′.由于C′不在∠MON内部,故人能从镜子里看见A、B两物体.
【规律总结】这道题是轴对称在实际中的应用,关键是建立相应轴对称图形的数学模型,再利用轴对称知识来解决.
方法5:拼图
【例6】如图所示,一批废料都是等腰三角形的小钢板,其中AB=AC,现要把这种废钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每块切割的次数最多两次,切割的损失忽略不计.
(1)请你设计两种不同的切割焊接方案,并且用简要的文字加以说明.
(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形应满足什么条件?
【解】(1)方案①、方案② 如图所示:
方案②中虚线为切割线,M、N为AB、AC中点,MP⊥BC.
(2)若要把该三角形只切割一次后焊接成正方形零件,则该三角形应为等腰直角三角形.
【规律总结】本题创新之处在于利用等腰三角形的对称性质进行切割后拼接成矩形,这种利用轴对称的性质解决实际生活中一些最优化方案的设计问题是中考的热点问题.
【例7】两个“十”字形纸板如图所示,每一个都由五个正方形组成,试将其中一个切成大小和形状相同的四块,与另一个“十”字形纸板拼合在一起,得到一个正方形.
【解】切拼方法如下:每块都完全一样.
四、中考试题归类解析
(一)判断图形是否是轴对称图形
【例1】(2003,北京市海淀区)羊年话“羊”字象征着美好和吉祥,下列图案都与“羊”字有关,其中是轴对称图形的个数是( )
A.1; B.2; B.3; D.4
【思路分析】沿着一条直线折叠后,直线两旁的部分能够互相重合的图形是第一个图和第三个图
【解】答案应是:B
【规律总结】判断一个图形是否是轴对称图形关键是根据定义来确定.
【例2】(2004,泸州)下列各种图形不是轴对称图形的是( )
【思路分析】沿着一条直线折叠,直线两旁的部分不能够互相重合的图形只有C图.
【解】应选:C.
【规律总结】要注意轴对称图形有时对称轴不只是一条.
(二)利用轴对称性质解题
【例1】(2004,河南)如图,直线L是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB∥CD ②AC⊥BD ③AO=OC ④AB⊥BC,其中正确的结论有_______.
【思路分析】因为L是四边形ABCD的对称轴可得到AB=AD、BC=DC,又因为AB=CD所以AB=AD=DC=CB可推出四边形ABCD为菱形,根据菱形性质可得出:AB∥CD;AC⊥BD、AO=OC.
故应填:①②③
【规律总结】解此类题的关键是要记住轴对称图形的性质.
【例2】(2003,南宁市)尺规:把右图(实线部分)补成以虚线L为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案(不用写作法、保留作图痕迹).
【解】
【规律总结】关于作轴对称图形一般是先作出对称点然后连接对称点得到对称图形.
五、中考试题集萃
一、填空题
1.(2003,吉林)下面四个图形中,从几何图形的性质考虑,哪一个与其他三个不同? 请指出这个图形,并简述你的理由.
答:图形__________;理由是__________.
2.(2003,安徽)如图1,L是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD ②AB=BC ③AB⊥BC ④AO=OC.其中正确的结论是_________.(把你认为正确的结论的序号都填上)
(1) (2) (3) (4)
3.(2004,南平)已知:如图2,在△ABC中,BC=8,AD是BC边上的高,D为垂足, 将△ABC折叠使点A与点D重合,则折痕EF的长为_________.
4.(2004,潍坊)如图3,请写出等腰梯形ABCD(AB∥CD).特有而一般梯形不具有的三个特征:__________;__________;_________.
5.(2003,长沙)如图4,请根据小文在镜中的像写出他的运动衣上的实际号码:_______.
二、选择题
1.(2003,河北省)下列图案中,有且只有三条对称轴的是( )
2.(2003,四川)我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下列我国四大银行的商标图案中是轴对称图形而不是中心对称图形的是( )
3.(2004,北京)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.等腰梯形 C.正方形 D.平行四边形
4.(2004,天津)在下列图形中,既是轴对称图形,又是中心对称图形的是( )
三、解答题
1.(2003,福州)用若干根火柴棒可以摆出一些优美的图案,下图是用火柴棒摆出的一个图案,此图案表示的含义可以是:天平(或公正).
请你用5根或5根以上火柴棒摆成一个轴对称图案,并说明你画出的图案的含义.
图案:
含义:
2.(2004,福州)图中是一个在19×16的点阵图上画出的“中国结”,点阵的每行及每列之间的距离都是1,请你画出“中国结”的对称轴,并直接写出图中阴影部分的面积.
3.(2004,陕西)已知:如图,在△ABC中,AB=BC=2∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).
(1)画出△ABC关于y轴对称的△A′B′C′;
(2)求以点A、B、B′、A′为顶点的四边形的面积.
答案:
一、填空题:
1.(1)② (2)四个图形中,只有图②不是轴对称图形.
2.①、②、④ 3.4 4.如∠A=∠B;∠C=∠D;AD=BC.是轴对称图形 5.108
二、选择题:1.D 2.C 3.C 4.C
三、解答题:
1.答案不惟一,略.
2.画出“中国结”的对称轴.
S=2×16×2=64
答:阴影部分的面积是64.
3.解:(1)画图正确
(2)过A点作AD⊥BC,交BC的延长线于点D,则
∠ABD=180°-∠ABC=180°-120°=60°
在Rt△ABD中
BD=AB·cos∠ABD=2×=1
AD=AB·sin∠ABD=2×=
又知点B的坐标为(-3,1)
∵点A的坐标为(-4,1+)
∵AA′⊥y轴,BB′⊥y轴 ∴AA′∥BB′
∵AB与A′B′不平行
∴以点A、B、B′、A′为顶点的四边形是等腰梯形
由点A、B的坐标可求得
AA′=2×4=8 BB′=2×3=6
∴梯形ABB′A′的面积=(AA′+BB′)·AD=×(8+6)×=7.毛
- 1 -
一、基础知识梳理
(一)主要概念
1.轴对称图形:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
角是轴对称图形,角平分线所在的直线是它的对称轴.
2.线段的垂直平分线:线段是轴对称图形,它的一条对称轴垂直于这条线段并且平分它,这样的直线叫做这条线段的垂直平分线(简称中垂线).
3.等腰三角形:有两条边相等的三角形叫做等腰三角形.
(二)主要性质
1.角的平分线上的点到这个角的两边的距离相等.
2.线段垂直平分线上的点到这条线段两个端点的距离相等.
3.等腰三角形是轴对称图形
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.等腰三角形的两个底角相等.
4.两个图形关于某条直线成轴对称,则对应点所连的线段被对称轴垂直平分.
对应线段相等,对就角相等.
二、考点与命题趋向分析
(一)能力
1.通过具体实例认识轴对称,探索它的基本性质,理解对应点所连的线段被对称轴垂直平分的性质.
2.能够按要求作出简单平面图形经过一次或两次轴对称后的图形;探索简单图形之间的轴对称关系,并能指出对称轴.
3.探索基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称性及其相关性质.
4.欣赏现实生活中的轴对称图形,结合现实生活中典型实例了解并欣赏物体的镜面对称,能利用轴对称进行图案设计.
5.了解角平分线及其性质.
6.了解线段垂直平分线及其性质.
7.了解等腰三角形的有关概念,探索并掌握等腰三角形的性质.
(二)命题趋向分析
1.中考中常在拼图中考查轴对称的有关概念,考查学生动手操作能力.
【例1】(2001年福建省福州市)两个全等的三角板,可以拼出各种不同的图形,图中已画出其中一个三角形,请你分别补出另一个与其全等的三角形,使每个图形分别成不同的轴对称图形(所画三角形可与原三角形有重叠部分).
【思路分析】只要对轴对称图形的概念清楚,弄清题意,本题还是很容易完成的,现举几例如下.
【解】
2.有些找规律题也利用轴对称图形出题.
【例2】(2004年烟台市)把26个英文字母按规律分成5组,现在还有5个字母D、M、Q、X、Z,请你按原规律补上,其顺序依次为( )
①F R P J L G □; ②H I O □
③N S □; ④B C K E □
⑤V A T Y W U □
A.Q X Z W D B.D M Q Z X C.Z X M D Q D.Q X Z D M
【思路分析】第①组不是中心对称图形,也不是轴对称图形,应填Q;
第②组既是中心对称图形,也是轴对称图形,应填X;
第③组是中心对称图形,不是轴对称图形,应填Z;
第④组不是中心对称图形,仅是轴对称图形,并且对称轴为一条水平线,应填D;
第⑤组也不是中心对称图形,仅是轴对称图形,并且对称轴为一条竖线,应填M.
【解】选D
三、解题方法与技巧
方法1:转化方法
【例1】如图所示,已知等腰三角形ABC,AB边的垂直平分线交AC于D,AB=AC=8,BC=6,求△BDC周长.
【解】∵DE是AB的垂直平分线
∴点B、A关于BD轴对称
∴AD=BD
∴△BCD的周长=BC+CD+BC=AD+CD+BC=AC+BC
∵AC=8,BC=6
∴△BCD周长=8+6=14.
【规律总结】本题的思路主要是将线段转化代换,把三角形周长转代为已知线段的和,这种转化的思想是解决数学问题的重要思想方法.
【例2】如图所示,在公路a同侧有两个居民小区A、B,现需要在公路旁建一个液化气站,要求到A、B的距离之和最短,这个液化气站应建在哪一个地方?
【解】已知直线a和a的同侧两点A、B,如同所示.
求作:点C,使C在直线a上,并且使AC+BC最小.
作法:1.作A点关于直线a的对称点A′.
2.连结A′B交直线a于点C,则C就是所求作的点.
【规律总结】本题通过作点A关于直线a的对称点A′,把AC+BC的和最短问题转化为A′、B两点之间线段最短的问题.
方法2:分类讨论法
【例3】如图所示,在四个正方形拼接的图形中,以这十个点中任意三点为顶点,共能组成________个等腰直角三角形,你愿意把得到上述结论的探究方法与他人交流吗?请在下面简要写出你的探究过程.
______________________________________________________________________________________________________。
【解】24个.以A1、A2、A3、A10、A9为直角顶点的等腰直角三角形分别有1个、1个、4个、5个、1个.共12个.再根据轴对称性质可知:在整个图形内共可组成12×2=24个等腰直角三角形.
方法3:数形结合法
【例4】如图所示,在正方形中均匀地分布着一些数字,小明利用轴对称的思想,用了一种非常巧妙的方法,迅速地将这组数字和求了出来,你也能试试吗?
【解】从数字组中可以看出,一条对角线上的数都是5,若把这条对角线当作对称轴,把正方形中的数之和为5×5+10×10=125.
方法4:构建数学模型
【例5】一面镜子MN竖直悬挂在墙壁上,人眼O的位置.如图所示,有三个物体A、B、C放在镜子前面,人眼能从镜子看见哪个物体?
【思路分析】物体在镜子里面所成的像就是数学问题中的物体关于镜面的对称点,人眼从镜子里所能看见的物体,它关于镜面的对称点,必须在眼的视线范围的.
【解】分别作A、B、C三点关于直线MN的对称点A′、B′、C′.由于C′不在∠MON内部,故人能从镜子里看见A、B两物体.
【规律总结】这道题是轴对称在实际中的应用,关键是建立相应轴对称图形的数学模型,再利用轴对称知识来解决.
方法5:拼图
【例6】如图所示,一批废料都是等腰三角形的小钢板,其中AB=AC,现要把这种废钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每块切割的次数最多两次,切割的损失忽略不计.
(1)请你设计两种不同的切割焊接方案,并且用简要的文字加以说明.
(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形应满足什么条件?
【解】(1)方案①、方案② 如图所示:
方案②中虚线为切割线,M、N为AB、AC中点,MP⊥BC.
(2)若要把该三角形只切割一次后焊接成正方形零件,则该三角形应为等腰直角三角形.
【规律总结】本题创新之处在于利用等腰三角形的对称性质进行切割后拼接成矩形,这种利用轴对称的性质解决实际生活中一些最优化方案的设计问题是中考的热点问题.
【例7】两个“十”字形纸板如图所示,每一个都由五个正方形组成,试将其中一个切成大小和形状相同的四块,与另一个“十”字形纸板拼合在一起,得到一个正方形.
【解】切拼方法如下:每块都完全一样.
四、中考试题归类解析
(一)判断图形是否是轴对称图形
【例1】(2003,北京市海淀区)羊年话“羊”字象征着美好和吉祥,下列图案都与“羊”字有关,其中是轴对称图形的个数是( )
A.1; B.2; B.3; D.4
【思路分析】沿着一条直线折叠后,直线两旁的部分能够互相重合的图形是第一个图和第三个图
【解】答案应是:B
【规律总结】判断一个图形是否是轴对称图形关键是根据定义来确定.
【例2】(2004,泸州)下列各种图形不是轴对称图形的是( )
【思路分析】沿着一条直线折叠,直线两旁的部分不能够互相重合的图形只有C图.
【解】应选:C.
【规律总结】要注意轴对称图形有时对称轴不只是一条.
(二)利用轴对称性质解题
【例1】(2004,河南)如图,直线L是四边形ABCD的对称轴,若AB=CD,有下面的结论:①AB∥CD ②AC⊥BD ③AO=OC ④AB⊥BC,其中正确的结论有_______.
【思路分析】因为L是四边形ABCD的对称轴可得到AB=AD、BC=DC,又因为AB=CD所以AB=AD=DC=CB可推出四边形ABCD为菱形,根据菱形性质可得出:AB∥CD;AC⊥BD、AO=OC.
故应填:①②③
【规律总结】解此类题的关键是要记住轴对称图形的性质.
【例2】(2003,南宁市)尺规:把右图(实线部分)补成以虚线L为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案(不用写作法、保留作图痕迹).
【解】
【规律总结】关于作轴对称图形一般是先作出对称点然后连接对称点得到对称图形.
五、中考试题集萃
一、填空题
1.(2003,吉林)下面四个图形中,从几何图形的性质考虑,哪一个与其他三个不同? 请指出这个图形,并简述你的理由.
答:图形__________;理由是__________.
2.(2003,安徽)如图1,L是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD ②AB=BC ③AB⊥BC ④AO=OC.其中正确的结论是_________.(把你认为正确的结论的序号都填上)
(1) (2) (3) (4)
3.(2004,南平)已知:如图2,在△ABC中,BC=8,AD是BC边上的高,D为垂足, 将△ABC折叠使点A与点D重合,则折痕EF的长为_________.
4.(2004,潍坊)如图3,请写出等腰梯形ABCD(AB∥CD).特有而一般梯形不具有的三个特征:__________;__________;_________.
5.(2003,长沙)如图4,请根据小文在镜中的像写出他的运动衣上的实际号码:_______.
二、选择题
1.(2003,河北省)下列图案中,有且只有三条对称轴的是( )
2.(2003,四川)我国主要银行的商标设计基本上都融入了中国古代钱币的图案,下列我国四大银行的商标图案中是轴对称图形而不是中心对称图形的是( )
3.(2004,北京)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.等腰梯形 C.正方形 D.平行四边形
4.(2004,天津)在下列图形中,既是轴对称图形,又是中心对称图形的是( )
三、解答题
1.(2003,福州)用若干根火柴棒可以摆出一些优美的图案,下图是用火柴棒摆出的一个图案,此图案表示的含义可以是:天平(或公正).
请你用5根或5根以上火柴棒摆成一个轴对称图案,并说明你画出的图案的含义.
图案:
含义:
2.(2004,福州)图中是一个在19×16的点阵图上画出的“中国结”,点阵的每行及每列之间的距离都是1,请你画出“中国结”的对称轴,并直接写出图中阴影部分的面积.
3.(2004,陕西)已知:如图,在△ABC中,AB=BC=2∠ABC=120°,BC∥x轴,点B的坐标是(-3,1).
(1)画出△ABC关于y轴对称的△A′B′C′;
(2)求以点A、B、B′、A′为顶点的四边形的面积.
答案:
一、填空题:
1.(1)② (2)四个图形中,只有图②不是轴对称图形.
2.①、②、④ 3.4 4.如∠A=∠B;∠C=∠D;AD=BC.是轴对称图形 5.108
二、选择题:1.D 2.C 3.C 4.C
三、解答题:
1.答案不惟一,略.
2.画出“中国结”的对称轴.
S=2×16×2=64
答:阴影部分的面积是64.
3.解:(1)画图正确
(2)过A点作AD⊥BC,交BC的延长线于点D,则
∠ABD=180°-∠ABC=180°-120°=60°
在Rt△ABD中
BD=AB·cos∠ABD=2×=1
AD=AB·sin∠ABD=2×=
又知点B的坐标为(-3,1)
∵点A的坐标为(-4,1+)
∵AA′⊥y轴,BB′⊥y轴 ∴AA′∥BB′
∵AB与A′B′不平行
∴以点A、B、B′、A′为顶点的四边形是等腰梯形
由点A、B的坐标可求得
AA′=2×4=8 BB′=2×3=6
∴梯形ABB′A′的面积=(AA′+BB′)·AD=×(8+6)×=7.毛
- 1 -
