6.3.1实数课件2022—2023学年人教版数学七年级下册(17张PPT)
文档属性
| 名称 | 6.3.1实数课件2022—2023学年人教版数学七年级下册(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 08:16:12 | ||
图片预览






文档简介
(共17张PPT)
敏而好学,不耻下问。
——孔子
课前准备:草稿本,笔,数学书,全品学习手册
1、请同学们回忆一下,我们学过哪些数? 举例说明。
导
2、 属于哪一类数呢?
学习目标:
1.了解无理数和实数的概念,掌握实数的分类.(重点)
2.知道实数和数轴上的点一一对应,进一步体会 “数形结合”
思想(难点)
6.3.1 实数
自学指导:自学课本P53-55的内容,思考并回答下列问题.
问题1:什么是实数?请你对实数进行分类。
问题2:实数与数轴上的点有什么关系?
问题3:如何求一个实数的相反数,绝对值?
学
议
1.学习之后你有什么疑惑,相互交流.
2.小组之间核对自学指导问题的答案,讨论梳理各问题的思路.
要求:组员积极讨论,展示并汇总易错点.
展
问题1 我们知道有理数包括整数和分数,把下列分数写成小数的形式,你有什么发现?
它们都可以写成有限小数或无限循环小数的形式
活动1 无理数和实数的概念,实数分类
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
展
想一想:所有的数都可以写成有限小数或无限循环小数的形式吗?
π=3.1415926535897932384626…
无限不循环小数叫做无理数.
不是.如:
1.01001000100001…(两个1之间依次多一个0)
活动1 无理数和实数的概念,实数分类
思考: 是无理数吗?
它是无限不循环小数,是无理数
常见的一些无理数:
(1)含 的一些数;
(2)开方开不尽的数;
(3)有规律但不循环的小数,如1.01001000100001…
有理数和无理数统称为实数
(两个1之间依次多一个0)
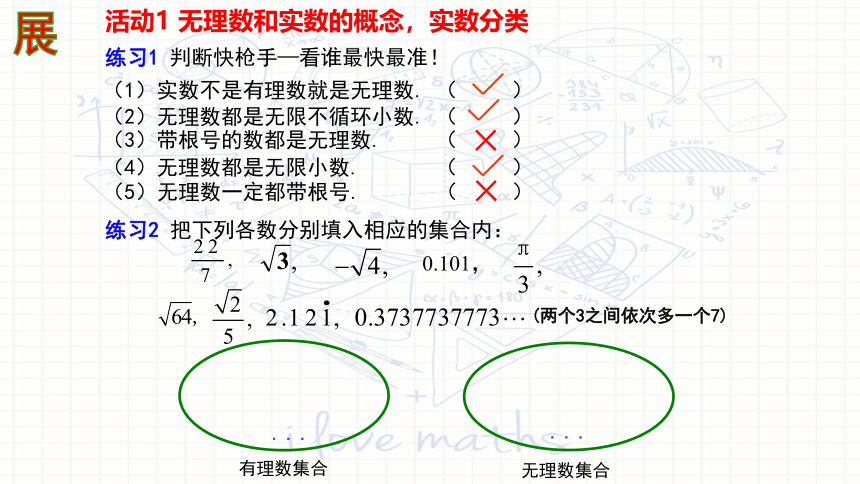
练习1 判断快枪手—看谁最快最准!
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
活动1 无理数和实数的概念,实数分类
练习2 把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
展
(两个3之间依次多一个7)
展
思考:我们将有理数和无理数统称为实数,类比有理数的分类方法,你能给实数分类吗?
无理数
有理数
实数
(1)按定义分
分数
整数
负无理数
正无理数
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
(2)按大小分
活动1 无理数和实数的概念,实数分类
无限不循环小数
有限小数或无限不循环小数
展
无理数:
有理数:
负实数:
正实数:
练习3 将下列各数分别填入下列相应的括号内:
活动1 无理数和实数的概念,实数分类
(两个3之间依次多一个2)
(两个3之间依次多一个2)
(两个3之间依次多一个2)
展
活动2 实数与数轴上的点的关系,及实数大小比较
思考1: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
因为圆的周长为π,所以数轴上点A表示的数是无理数π.
思考2:你能在数轴上表示出 和- 吗?
1
1
1
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
★实数和数轴上的点是一一对应的.
活动2 实数与数轴上的点的关系,及实数大小比较
展
每一个无理数都可以用数轴上的一个点来表示;
与规定有理数的大小一样,对于数轴上任意的两个点,右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
展
练习4 我们知道实数和数轴上的点一一对应,如下图,正方形的边长为1,以数轴上表示数1的点为圆心,正方形的对角线长为半径画弧,与数轴正半轴交于点P,则点P对应的实数为( )
A. B. C.2.4 D.2.5
B
-2 -1 0 1 2 3
1
-2
-2< < 1< <
解:如图所示:
用“<”连接为:
练习5 在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
活动3 求实数的相反数、绝对值
思考:(1) 的相反数是_____,-π的相反数是_____,0的相反数是_____;
(2) _______, |-π| =_____, |0|= _____.
0
π
0
π
有理数关于相反数和绝对值的意义同样适合于实数。
1、a是一个实数,数a的相反数为-a.
2、①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③0的绝对值是0.
展
展
2和-2
活动3 求实数的相反数、绝对值
1.下列实数中,是无理数的为( )
3.-的相反数是 ;绝对值是 -= .
C
4.将实数√5,π,0,-6由小到大用“<”号连接起来: .
A
测
测
④⑥⑦⑧
①⑤⑥⑧
③④
②⑦
实数
无理数:无限不循环小数
实数:有理数和无理数的统称
实数的分类
实数的数轴表示
实数的大小比较
作业布置 完成《全品》课时作业(十七)
理
求实数的相反数、绝对值
敏而好学,不耻下问。
——孔子
课前准备:草稿本,笔,数学书,全品学习手册
1、请同学们回忆一下,我们学过哪些数? 举例说明。
导
2、 属于哪一类数呢?
学习目标:
1.了解无理数和实数的概念,掌握实数的分类.(重点)
2.知道实数和数轴上的点一一对应,进一步体会 “数形结合”
思想(难点)
6.3.1 实数
自学指导:自学课本P53-55的内容,思考并回答下列问题.
问题1:什么是实数?请你对实数进行分类。
问题2:实数与数轴上的点有什么关系?
问题3:如何求一个实数的相反数,绝对值?
学
议
1.学习之后你有什么疑惑,相互交流.
2.小组之间核对自学指导问题的答案,讨论梳理各问题的思路.
要求:组员积极讨论,展示并汇总易错点.
展
问题1 我们知道有理数包括整数和分数,把下列分数写成小数的形式,你有什么发现?
它们都可以写成有限小数或无限循环小数的形式
活动1 无理数和实数的概念,实数分类
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
展
想一想:所有的数都可以写成有限小数或无限循环小数的形式吗?
π=3.1415926535897932384626…
无限不循环小数叫做无理数.
不是.如:
1.01001000100001…(两个1之间依次多一个0)
活动1 无理数和实数的概念,实数分类
思考: 是无理数吗?
它是无限不循环小数,是无理数
常见的一些无理数:
(1)含 的一些数;
(2)开方开不尽的数;
(3)有规律但不循环的小数,如1.01001000100001…
有理数和无理数统称为实数
(两个1之间依次多一个0)
练习1 判断快枪手—看谁最快最准!
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
活动1 无理数和实数的概念,实数分类
练习2 把下列各数分别填入相应的集合内:
0.101,
有理数集合
无理数集合
...
...
展
(两个3之间依次多一个7)
展
思考:我们将有理数和无理数统称为实数,类比有理数的分类方法,你能给实数分类吗?
无理数
有理数
实数
(1)按定义分
分数
整数
负无理数
正无理数
负实数
正实数
数实
正有理数
负有理数
0
正无理数
负无理数
(2)按大小分
活动1 无理数和实数的概念,实数分类
无限不循环小数
有限小数或无限不循环小数
展
无理数:
有理数:
负实数:
正实数:
练习3 将下列各数分别填入下列相应的括号内:
活动1 无理数和实数的概念,实数分类
(两个3之间依次多一个2)
(两个3之间依次多一个2)
(两个3之间依次多一个2)
展
活动2 实数与数轴上的点的关系,及实数大小比较
思考1: 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
●
A
因为圆的周长为π,所以数轴上点A表示的数是无理数π.
思考2:你能在数轴上表示出 和- 吗?
1
1
1
-2
-1
0
1
2
-
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
★实数和数轴上的点是一一对应的.
活动2 实数与数轴上的点的关系,及实数大小比较
展
每一个无理数都可以用数轴上的一个点来表示;
与规定有理数的大小一样,对于数轴上任意的两个点,右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
展
练习4 我们知道实数和数轴上的点一一对应,如下图,正方形的边长为1,以数轴上表示数1的点为圆心,正方形的对角线长为半径画弧,与数轴正半轴交于点P,则点P对应的实数为( )
A. B. C.2.4 D.2.5
B
-2 -1 0 1 2 3
1
-2
-2< < 1< <
解:如图所示:
用“<”连接为:
练习5 在数轴上表示下列各点,比较它们的大小,并用“<”连接它们.
活动3 求实数的相反数、绝对值
思考:(1) 的相反数是_____,-π的相反数是_____,0的相反数是_____;
(2) _______, |-π| =_____, |0|= _____.
0
π
0
π
有理数关于相反数和绝对值的意义同样适合于实数。
1、a是一个实数,数a的相反数为-a.
2、①一个正实数的绝对值是它本身;
②一个负实数的绝对值是它的相反数;
③0的绝对值是0.
展
展
2和-2
活动3 求实数的相反数、绝对值
1.下列实数中,是无理数的为( )
3.-的相反数是 ;绝对值是 -= .
C
4.将实数√5,π,0,-6由小到大用“<”号连接起来: .
A
测
测
④⑥⑦⑧
①⑤⑥⑧
③④
②⑦
实数
无理数:无限不循环小数
实数:有理数和无理数的统称
实数的分类
实数的数轴表示
实数的大小比较
作业布置 完成《全品》课时作业(十七)
理
求实数的相反数、绝对值
