勾股定理的证明[上学期]
图片预览



文档简介
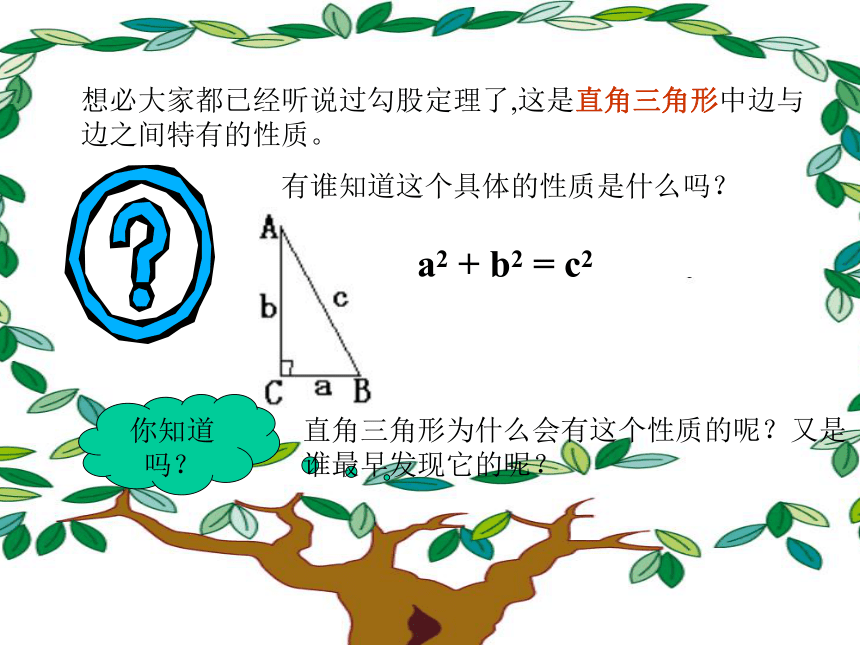
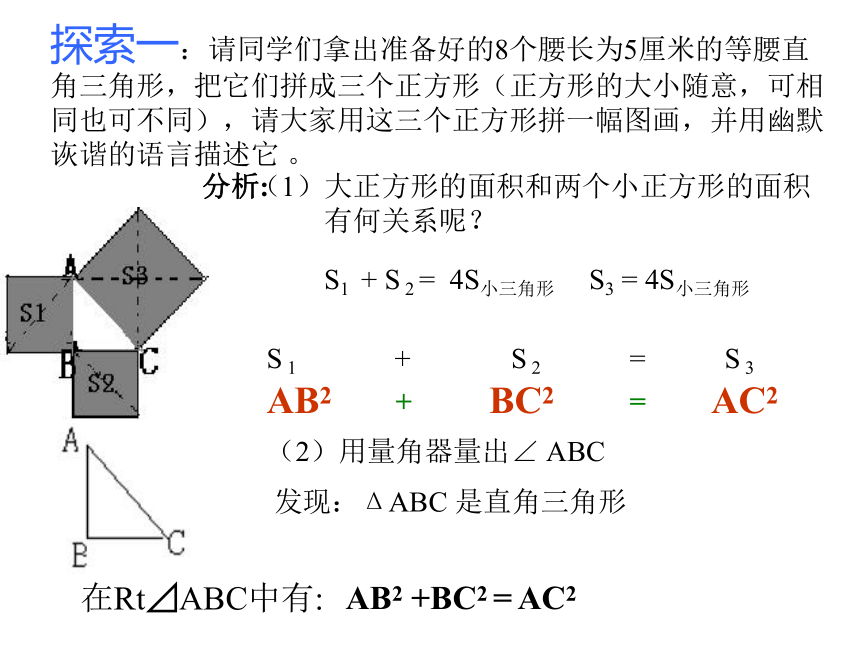
课件16张PPT。19.2勾股定理(一)西门中学 岑晓玲想必大家都已经听说过勾股定理了,这是直角三角形中边与边之间特有的性质。有谁知道这个具体的性质是什么吗?a2 + b2 = c2你知道吗?直角三角形为什么会有这个性质的呢?又是谁最早发现它的呢?探索一:请同学们拿出准备好的8个腰长为5厘米的等腰直
角三角形,把它们拼成三个正方形(正方形的大小随意,可相
同也可不同),请大家用这三个正方形拼一幅图画,并用幽默
诙谐的语言描述它 。(1)大正方形的面积和两个小正方形的面积
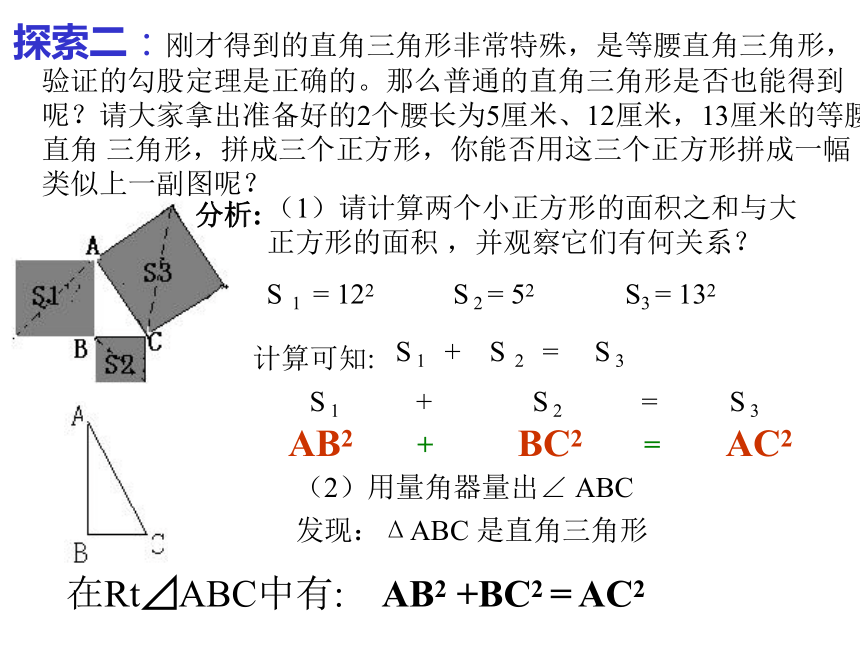
有何关系呢? S1 + S 2 = 4S小三角形S3 = 4S小三角形(2)用量角器量出∠ ABC发现:ΔABC 是直角三角形AB2 +BC2 = AC2在Rt⊿ABC中有:分析:S 1 + S 2 = S 3AB2BC2AC2+ = 探索二:刚才得到的直角三角形非常特殊,是等腰直角三角形,
验证的勾股定理是正确的。那么普通的直角三角形是否也能得到
呢?请大家拿出准备好的2个腰长为5厘米、12厘米,13厘米的等腰
直角 三角形,拼成三个正方形,你能否用这三个正方形拼成一幅
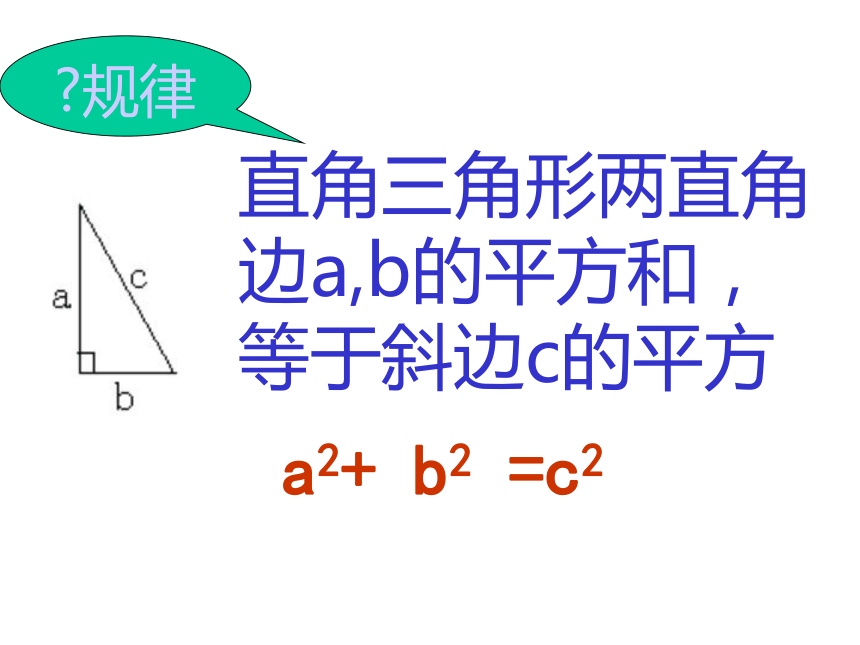
类似上一副图呢?(1)请计算两个小正方形的面积之和与大正方形的面积 ,并观察它们有何关系?S 1 = 122 S 2 = 52S3 = 132S 1 + S 2 = S 3AB2 +BC2 = AC2在Rt⊿ABC中有:(2)用量角器量出∠ ABC计算可知:发现:ΔABC 是直角三角形 S 1 + S 2 = S 3AB2+BC2 = AC2分析:?规律直角三角形两直角边a,b的平方和,等于斜边c的平方a2+ b2 =c2 做一做请在课本中的方格图中,用三角尺画出两条直角边分别是5cm, 12cm的直角三角形,然后用刻度尺量出斜边长想一想:你能在测量之前猜想出斜边长吗?
经测量可知:斜边的长度也为13厘米左右。斜边2 = 52 + 122 = 169所以 斜边 = 13 (厘米) 毕达哥拉斯定理
西方人认为最早发现直角三角形具有“勾2+股2=弦2”这一性质并且最先给出严格证明的是古希腊的数学家毕达哥拉斯(Pythagoras)我国至今可查的有关勾股定理的最早记载,是大约公元前1世纪前后成书的《周髀算经》比毕达哥拉斯要早发现500多年。勾股定理
直角三角形两直角边 a,b的平方和,等于斜边c的平方. 即 a2+ b2 =c2a2 + b2c2 - b2c2 - a2如果直角三角形知道其中两边 ,是否一定可以得出第三边呢?=c2 =a2=b2 比一比,看谁做的快 32511464如图,在Rt△ABC中, ∠c = 90°因为 2a = 3b , 所以a = b 由a2 + b2 = c2 得:: b = 4 例2:如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)分析:先把实际问题转化成数学问题。求:AB的长。解:在Rt⊿ABC中,∠ABC = 90o ,
BC = 2.16 , CA = 5.41
根据勾股定理得: AB =答:梯子上端A到墙的底端B的距离AB长约4.96米。(米) 勾股定理
1、 Rt△中边与边的关系 两直角
边的平方和 等于斜边的平方2、在Rt△ABC中,根据勾股定理 :
c2=a2+b2
a2=c2-b2
b2=c2-a2 小结想一想:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt⊿ABC中,∠BAC = 90o ,所以有: ( x + 0.5 )2 = x2 + 22画一画 :你能在格点图中画出面积
为169的正方形吗?在做一做中我们已经会在格点图中
画出斜边长为13的直角三角形了。
角三角形,把它们拼成三个正方形(正方形的大小随意,可相
同也可不同),请大家用这三个正方形拼一幅图画,并用幽默
诙谐的语言描述它 。(1)大正方形的面积和两个小正方形的面积
有何关系呢? S1 + S 2 = 4S小三角形S3 = 4S小三角形(2)用量角器量出∠ ABC发现:ΔABC 是直角三角形AB2 +BC2 = AC2在Rt⊿ABC中有:分析:S 1 + S 2 = S 3AB2BC2AC2+ = 探索二:刚才得到的直角三角形非常特殊,是等腰直角三角形,
验证的勾股定理是正确的。那么普通的直角三角形是否也能得到
呢?请大家拿出准备好的2个腰长为5厘米、12厘米,13厘米的等腰
直角 三角形,拼成三个正方形,你能否用这三个正方形拼成一幅
类似上一副图呢?(1)请计算两个小正方形的面积之和与大正方形的面积 ,并观察它们有何关系?S 1 = 122 S 2 = 52S3 = 132S 1 + S 2 = S 3AB2 +BC2 = AC2在Rt⊿ABC中有:(2)用量角器量出∠ ABC计算可知:发现:ΔABC 是直角三角形 S 1 + S 2 = S 3AB2+BC2 = AC2分析:?规律直角三角形两直角边a,b的平方和,等于斜边c的平方a2+ b2 =c2 做一做请在课本中的方格图中,用三角尺画出两条直角边分别是5cm, 12cm的直角三角形,然后用刻度尺量出斜边长想一想:你能在测量之前猜想出斜边长吗?
经测量可知:斜边的长度也为13厘米左右。斜边2 = 52 + 122 = 169所以 斜边 = 13 (厘米) 毕达哥拉斯定理
西方人认为最早发现直角三角形具有“勾2+股2=弦2”这一性质并且最先给出严格证明的是古希腊的数学家毕达哥拉斯(Pythagoras)我国至今可查的有关勾股定理的最早记载,是大约公元前1世纪前后成书的《周髀算经》比毕达哥拉斯要早发现500多年。勾股定理
直角三角形两直角边 a,b的平方和,等于斜边c的平方. 即 a2+ b2 =c2a2 + b2c2 - b2c2 - a2如果直角三角形知道其中两边 ,是否一定可以得出第三边呢?=c2 =a2=b2 比一比,看谁做的快 32511464如图,在Rt△ABC中, ∠c = 90°因为 2a = 3b , 所以a = b 由a2 + b2 = c2 得:: b = 4 例2:如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)分析:先把实际问题转化成数学问题。求:AB的长。解:在Rt⊿ABC中,∠ABC = 90o ,
BC = 2.16 , CA = 5.41
根据勾股定理得: AB =答:梯子上端A到墙的底端B的距离AB长约4.96米。(米) 勾股定理
1、 Rt△中边与边的关系 两直角
边的平方和 等于斜边的平方2、在Rt△ABC中,根据勾股定理 :
c2=a2+b2
a2=c2-b2
b2=c2-a2 小结想一想:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt⊿ABC中,∠BAC = 90o ,所以有: ( x + 0.5 )2 = x2 + 22画一画 :你能在格点图中画出面积
为169的正方形吗?在做一做中我们已经会在格点图中
画出斜边长为13的直角三角形了。
