勾股定理[上学期]
图片预览


文档简介
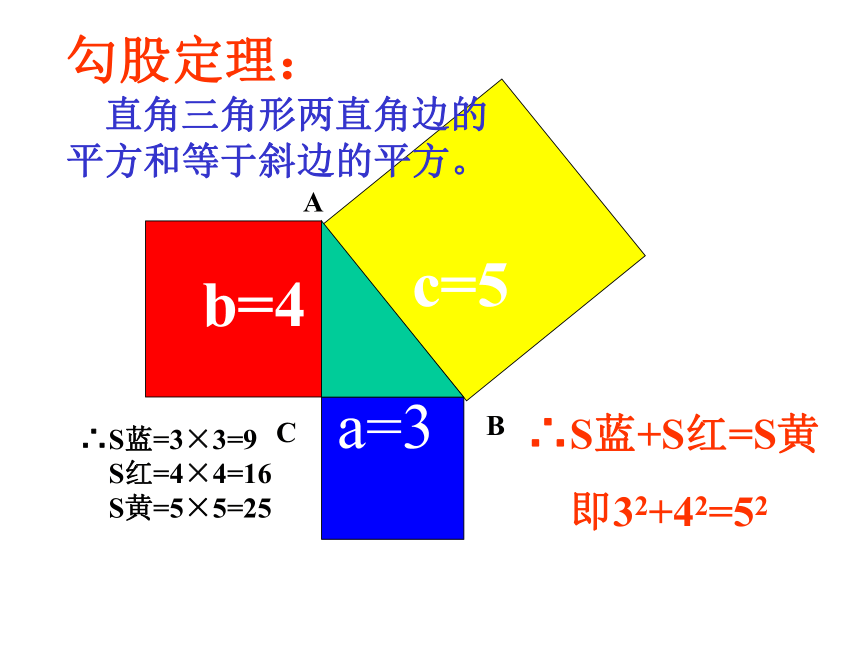
课件8张PPT。19.2勾股定理ABCa=3b=4c=5∴S蓝=3×3=9
S红=4×4=16
S黄=5×5=25∴S蓝+S红=S黄
即32+42=52勾股定理:
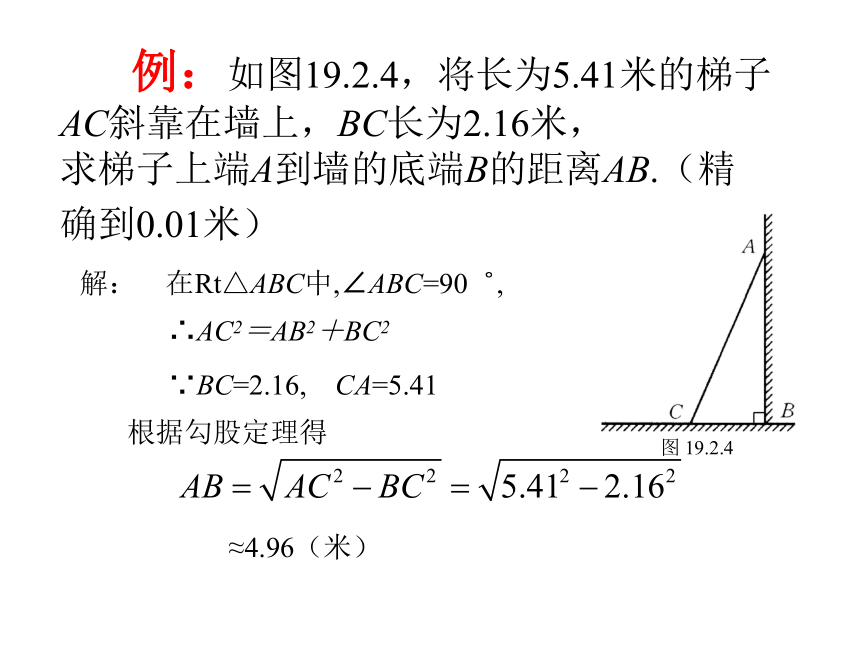
直角三角形两直角边的平方和等于斜边的平方。勾股史话:我国古代:公元前1100多年《周髀算经》古埃及:公元25世纪前,金字塔底部的直角三角形古希腊:公元前550年,毕达哥拉斯定理 例:如图19.2.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米, 求梯子上端A到墙的底端B的距离AB.(精确到0.01米) 解: 在Rt△ABC中,∠ABC=90゜, ∴AC2=AB2+BC2∵BC=2.16, CA=5.41 根据勾股定理得
≈4.96(米) 练习:在Rt△ABC中,AB=c,BC=a,AC=b, ∠B=90゜.
(1)已知a=6,b=10,求c;?
(2)已知a=24,c=25,求b1、在Rt△ABC中,AB=c,BC=a,AC=b, 若a=6, b=8,则:
(1) 当∠C=90゜时,c= ;
(2) 当∠B=90゜时,c= 。2、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?巩固练习:引葭(jia)赴岸:“今有池方一丈,葭生其中央分水一尺,引葭赴岸适与岸齐,问水深,葭长各几何.”本题的意思是:有一水池一丈见方,池中间生有棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?思考题:
1、等腰三角形的面积为8,则 它的周长是多少? 2、一段楼梯,高BC是2米,斜边AB为4米,在楼梯上铺地毯,至少需要 米
S红=4×4=16
S黄=5×5=25∴S蓝+S红=S黄
即32+42=52勾股定理:
直角三角形两直角边的平方和等于斜边的平方。勾股史话:我国古代:公元前1100多年《周髀算经》古埃及:公元25世纪前,金字塔底部的直角三角形古希腊:公元前550年,毕达哥拉斯定理 例:如图19.2.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米, 求梯子上端A到墙的底端B的距离AB.(精确到0.01米) 解: 在Rt△ABC中,∠ABC=90゜, ∴AC2=AB2+BC2∵BC=2.16, CA=5.41 根据勾股定理得
≈4.96(米) 练习:在Rt△ABC中,AB=c,BC=a,AC=b, ∠B=90゜.
(1)已知a=6,b=10,求c;?
(2)已知a=24,c=25,求b1、在Rt△ABC中,AB=c,BC=a,AC=b, 若a=6, b=8,则:
(1) 当∠C=90゜时,c= ;
(2) 当∠B=90゜时,c= 。2、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?巩固练习:引葭(jia)赴岸:“今有池方一丈,葭生其中央分水一尺,引葭赴岸适与岸齐,问水深,葭长各几何.”本题的意思是:有一水池一丈见方,池中间生有棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?思考题:
1、等腰三角形的面积为8,则 它的周长是多少? 2、一段楼梯,高BC是2米,斜边AB为4米,在楼梯上铺地毯,至少需要 米
