勾股定理1[上学期]
图片预览





文档简介
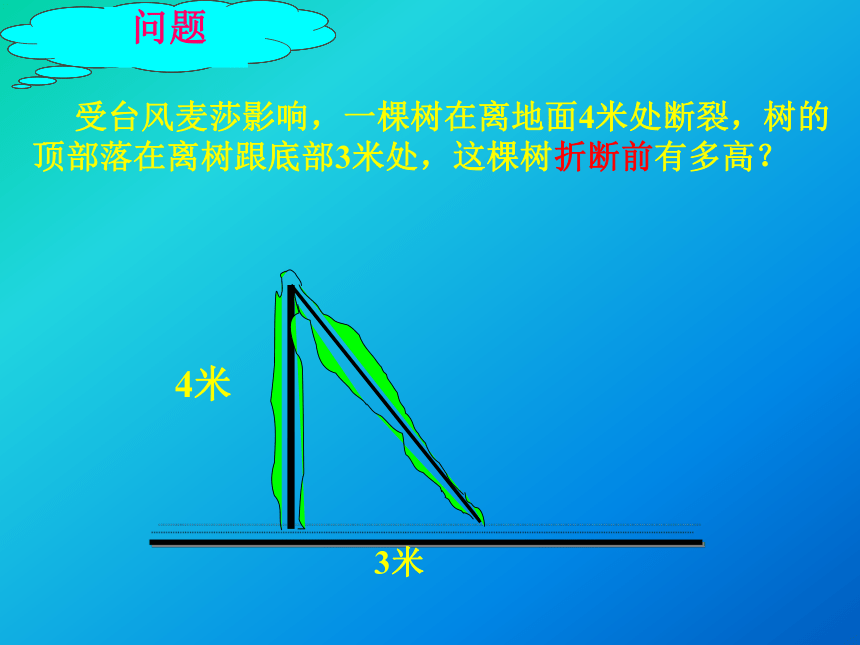
课件21张PPT。八年级数学(下册)? 华师大版勾股定理下管中学 喻爱国 受台风麦莎影响,一棵树在离地面4米处断裂,树的
顶部落在离树跟底部3米处,这棵树折断前有多高?
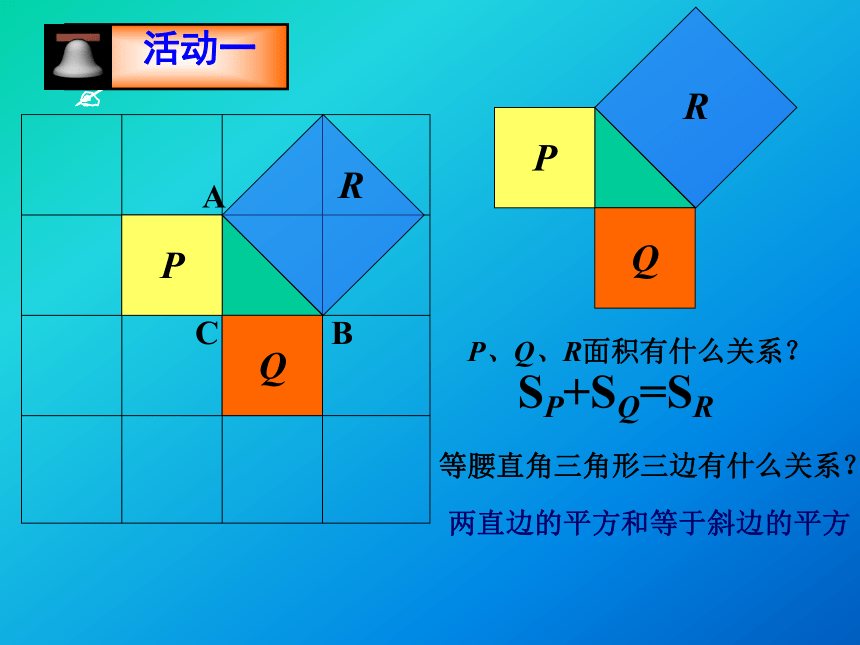
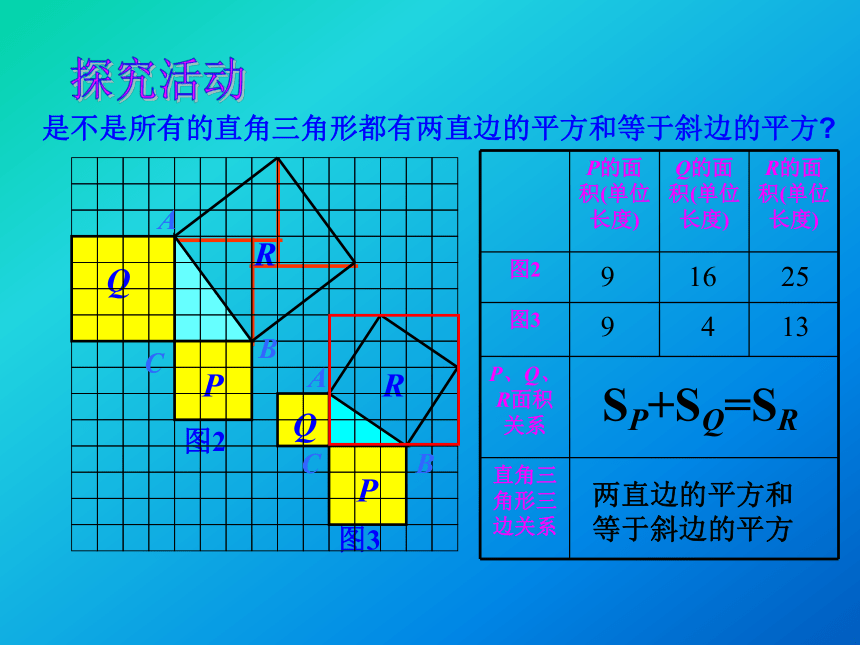
问题QPP、Q、R面积有什么关系?SP+SQ=SR等腰直角三角形三边有什么关系?两直边的平方和等于斜边的平方探究活动是不是所有的直角三角形都有两直边的平方和等于斜边的平方?916259413SP+SQ=SR两直边的平方和
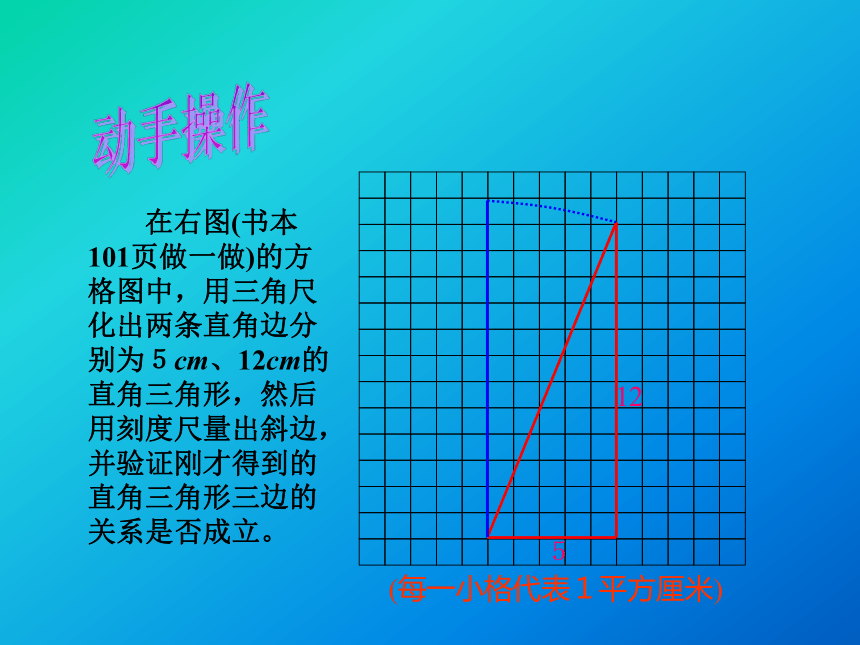
等于斜边的平方动手操作 在右图(书本101页做一做)的方格图中,用三角尺化出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边,并验证刚才得到的直角三角形三边的关系是否成立。(每一小格代表1平方厘米)512 勾股定理(gou-gu theorem) 如果直角三角形两直角边分别为a、b,斜边为c,那么 即 直角三角形两直角边的平方和等于斜边的平方.在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾弦股商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。
这就是著名的勾股定理.勾股定理毕达哥拉斯定理Pythagoras’ theorem毕达哥拉斯在国外,相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 c2=a2 + b2a2=c2 - b2b2 =a2 -c2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 例1 如图,将长5.41米的梯子AC斜靠在墙上,
BC长为2.16米,求梯子上端A到墙的底边的垂直
距离AB。(精确到0.01米)问题解决 受台风麦莎影响,一棵树在离地面4米处断裂,树的
顶部落在离树跟底部3米处,这棵树折断前有多高?
例2:如图,引葭赴岸:“今有池方一丈,葭生其中央
分水一尺,引葭赴岸适与岸齐,问水深,葭长各几何。” 意思:有一个水池一丈见
方,池中间生有一棵芦苇,露
出水面一尺,如把它引向岸边,
正好与岸边齐,问水有多深,
芦苇有多长?错例辨析 △ABC的两边为3和4,求第三边
解:由于三角形的两边为3、4
所以它的第三边的c应满足
c2=32+42=25
即:c=5
辨析:(1)要用勾股定理解题,首先应具备直角三角形
这个必不可少的条件,可本题△ABC并未说明它是否是直
角三角形,所以用勾股定理就没有依据。
(2)若告诉△ABC是直角三角形,第三边c也不一定是满
足c2=a2+b2 ,题目中并没有交待c 是斜边,综上所述这个
题目条件不足,第三边无法求得 练一练 如图,已知等边三角形ABC的边长为2,求BC边上的高AD的长度?比一比,看谁做的快 如图,在Rt△ABC中,
∠c = 90°3251141、求下列2个三角形中的第三条边的长。2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米?A1312?小结:1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)P的面积+Q的面积=R的面积a2+b2=c2再见谢谢大家
顶部落在离树跟底部3米处,这棵树折断前有多高?
问题QPP、Q、R面积有什么关系?SP+SQ=SR等腰直角三角形三边有什么关系?两直边的平方和等于斜边的平方探究活动是不是所有的直角三角形都有两直边的平方和等于斜边的平方?916259413SP+SQ=SR两直边的平方和
等于斜边的平方动手操作 在右图(书本101页做一做)的方格图中,用三角尺化出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边,并验证刚才得到的直角三角形三边的关系是否成立。(每一小格代表1平方厘米)512 勾股定理(gou-gu theorem) 如果直角三角形两直角边分别为a、b,斜边为c,那么 即 直角三角形两直角边的平方和等于斜边的平方.在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾弦股商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。
这就是著名的勾股定理.勾股定理毕达哥拉斯定理Pythagoras’ theorem毕达哥拉斯在国外,相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 c2=a2 + b2a2=c2 - b2b2 =a2 -c2结论变形直角三角形中,两直角边的平方和等于斜边的平方; 例1 如图,将长5.41米的梯子AC斜靠在墙上,
BC长为2.16米,求梯子上端A到墙的底边的垂直
距离AB。(精确到0.01米)问题解决 受台风麦莎影响,一棵树在离地面4米处断裂,树的
顶部落在离树跟底部3米处,这棵树折断前有多高?
例2:如图,引葭赴岸:“今有池方一丈,葭生其中央
分水一尺,引葭赴岸适与岸齐,问水深,葭长各几何。” 意思:有一个水池一丈见
方,池中间生有一棵芦苇,露
出水面一尺,如把它引向岸边,
正好与岸边齐,问水有多深,
芦苇有多长?错例辨析 △ABC的两边为3和4,求第三边
解:由于三角形的两边为3、4
所以它的第三边的c应满足
c2=32+42=25
即:c=5
辨析:(1)要用勾股定理解题,首先应具备直角三角形
这个必不可少的条件,可本题△ABC并未说明它是否是直
角三角形,所以用勾股定理就没有依据。
(2)若告诉△ABC是直角三角形,第三边c也不一定是满
足c2=a2+b2 ,题目中并没有交待c 是斜边,综上所述这个
题目条件不足,第三边无法求得 练一练 如图,已知等边三角形ABC的边长为2,求BC边上的高AD的长度?比一比,看谁做的快 如图,在Rt△ABC中,
∠c = 90°3251141、求下列2个三角形中的第三条边的长。2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米?A1312?小结:1、利用数格子的方法,探索了以直角三角形三边为边长的正方形面积的关系(即两个小正方形的面积之和等于大正方形的面积)P的面积+Q的面积=R的面积a2+b2=c2再见谢谢大家
