勾股定理1[上学期]
图片预览
文档简介
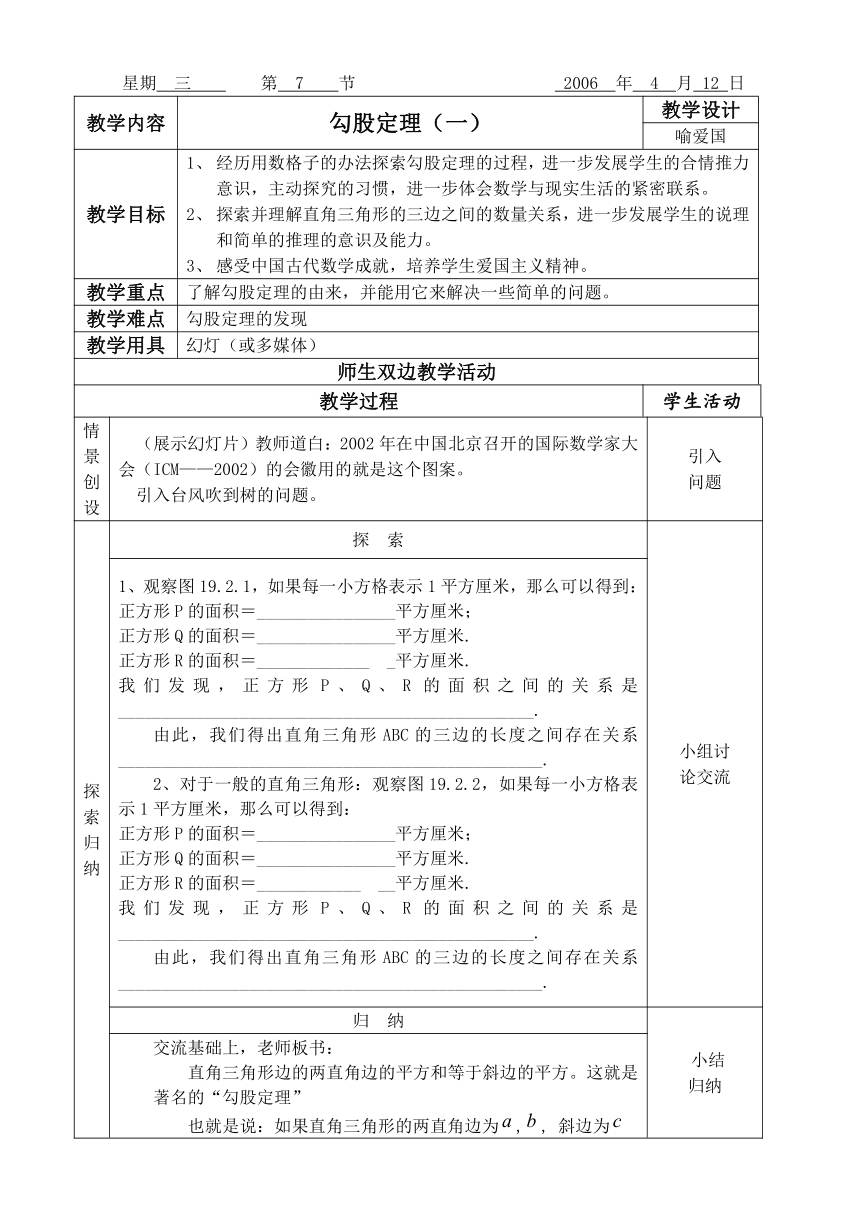
星期 三 第 7 节 2006 年 4 月 12 日
教学内容 勾股定理(一) 教学设计
喻爱国
教学目标 经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推力意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。感受中国古代数学成就,培养学生爱国主义精神。
教学重点 了解勾股定理的由来,并能用它来解决一些简单的问题。
教学难点 勾股定理的发现
教学用具 幻灯(或多媒体)
师生双边教学活动
教学过程 学生活动
情景创设 (展示幻灯片)教师道白:2002年在中国北京召开的国际数学家大会(ICM——2002)的会徽用的就是这个图案。引入台风吹到树的问题。 引入问题
探索归纳 探 索 小组讨论交流
1、观察图19.2.1,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面积=________________平方厘米;正方形Q的面积=________________平方厘米.正方形R的面积=_____________ _平方厘米.我们发现,正方形P、Q、R的面积之间的关系是________________________________________________.由此,我们得出直角三角形ABC的三边的长度之间存在关系_________________________________________________.2、对于一般的直角三角形:观察图19.2.2,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面积=________________平方厘米;正方形Q的面积=________________平方厘米.正方形R的面积=____________ __平方厘米.我们发现,正方形P、Q、R的面积之间的关系是________________________________________________.由此,我们得出直角三角形ABC的三边的长度之间存在关系_________________________________________________.
归 纳 小结归纳
交流基础上,老师板书:直角三角形边的两直角边的平方和等于斜边的平方。这就是著名的“勾股定理”也就是说:如果直角三角形的两直角边为,, 斜边为那么我国古代称直角三角形的较短的直角边为勾,较长的为股,斜边为弦,这就是勾股定理的由来。简单介绍中国古代和西方国家对勾股定理的认识。
例题讲解 例1:如图19.2.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米) 例2:如图,引葭赴岸:“今有池方一丈,葭生其中央分水一尺,引葭赴岸适与岸齐,问水深,葭长各几何。” 寻找已知条件列式求解
巩固练习 基础巩固 练习思考
在Rt△ABC中,AB=c,BC=a,AC=b, ∠B=90゜.(1) 已知a=6,b=10,求c; (2) 已知a=24,c=25,求b。如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?3. 错例辨析:△ABC的两边为3和4,求第三边解:由于三角形的两边为3、4所以它的第三边的c应满足即:
能力提升
1、已知等边三角形ABC的边长为2,求BC边上的高AD的长度?2、比一比,看谁做的快
概括总结 这节课我们通过具体的实例验证了直角三角形三边之间的关系,实际上,勾股定理在我国古代早已被发现和运用,今天我们只不过做了粗略的探讨,通过本节课的学习,同学们一方面要掌握勾股定理的 内容,另一方面要能用它来计算直角三角形边的长度。 回顾总结
布置作业 见作业本 课后反思
教学内容 勾股定理(一) 教学设计
喻爱国
教学目标 经历用数格子的办法探索勾股定理的过程,进一步发展学生的合情推力意识,主动探究的习惯,进一步体会数学与现实生活的紧密联系。探索并理解直角三角形的三边之间的数量关系,进一步发展学生的说理和简单的推理的意识及能力。感受中国古代数学成就,培养学生爱国主义精神。
教学重点 了解勾股定理的由来,并能用它来解决一些简单的问题。
教学难点 勾股定理的发现
教学用具 幻灯(或多媒体)
师生双边教学活动
教学过程 学生活动
情景创设 (展示幻灯片)教师道白:2002年在中国北京召开的国际数学家大会(ICM——2002)的会徽用的就是这个图案。引入台风吹到树的问题。 引入问题
探索归纳 探 索 小组讨论交流
1、观察图19.2.1,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面积=________________平方厘米;正方形Q的面积=________________平方厘米.正方形R的面积=_____________ _平方厘米.我们发现,正方形P、Q、R的面积之间的关系是________________________________________________.由此,我们得出直角三角形ABC的三边的长度之间存在关系_________________________________________________.2、对于一般的直角三角形:观察图19.2.2,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面积=________________平方厘米;正方形Q的面积=________________平方厘米.正方形R的面积=____________ __平方厘米.我们发现,正方形P、Q、R的面积之间的关系是________________________________________________.由此,我们得出直角三角形ABC的三边的长度之间存在关系_________________________________________________.
归 纳 小结归纳
交流基础上,老师板书:直角三角形边的两直角边的平方和等于斜边的平方。这就是著名的“勾股定理”也就是说:如果直角三角形的两直角边为,, 斜边为那么我国古代称直角三角形的较短的直角边为勾,较长的为股,斜边为弦,这就是勾股定理的由来。简单介绍中国古代和西方国家对勾股定理的认识。
例题讲解 例1:如图19.2.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米) 例2:如图,引葭赴岸:“今有池方一丈,葭生其中央分水一尺,引葭赴岸适与岸齐,问水深,葭长各几何。” 寻找已知条件列式求解
巩固练习 基础巩固 练习思考
在Rt△ABC中,AB=c,BC=a,AC=b, ∠B=90゜.(1) 已知a=6,b=10,求c; (2) 已知a=24,c=25,求b。如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?3. 错例辨析:△ABC的两边为3和4,求第三边解:由于三角形的两边为3、4所以它的第三边的c应满足即:
能力提升
1、已知等边三角形ABC的边长为2,求BC边上的高AD的长度?2、比一比,看谁做的快
概括总结 这节课我们通过具体的实例验证了直角三角形三边之间的关系,实际上,勾股定理在我国古代早已被发现和运用,今天我们只不过做了粗略的探讨,通过本节课的学习,同学们一方面要掌握勾股定理的 内容,另一方面要能用它来计算直角三角形边的长度。 回顾总结
布置作业 见作业本 课后反思
