勾股定理[上学期]
图片预览


文档简介
课件16张PPT。2006年3月19.2勾股定理蔡璞先一、新课导入:
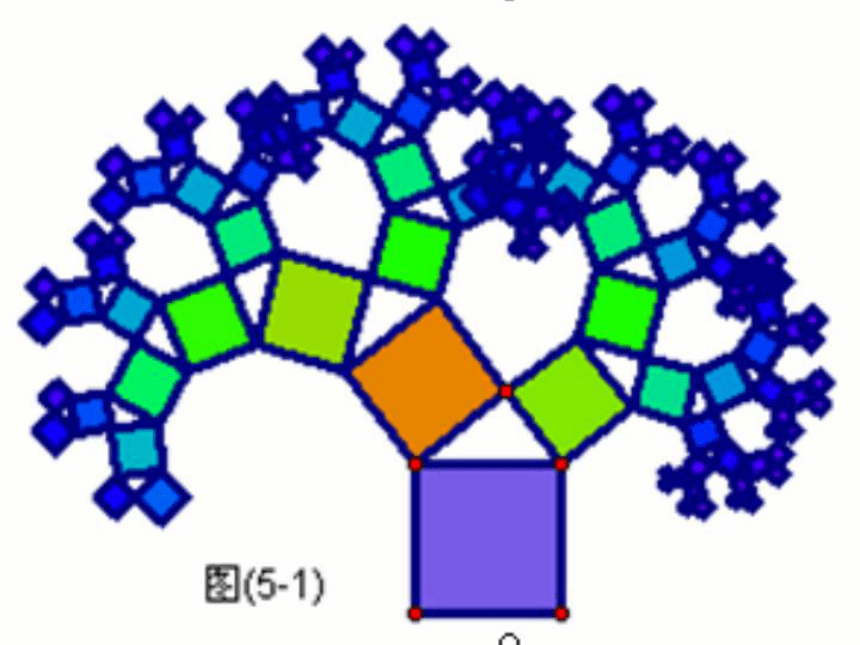
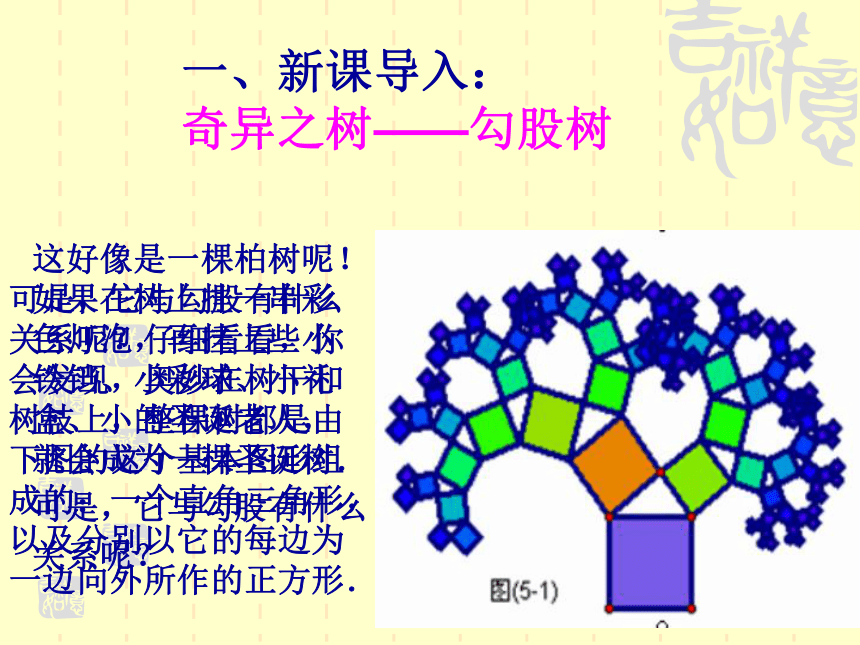
奇异之树——勾股树这好像是一棵柏树呢!
如果在树上挂一串彩
色灯泡,再挂上些小
铃铛、小彩球、小礼
盒、小的圣诞老人,
就会成为一棵圣诞树.
可是,它与勾股有什么
关系呢?
可是,它与勾股有什么
关系呢?仔细看看,你
会发现,奥妙在树干和
树枝上,整棵树都是由
下图的这个基本图形组
成的:一个直角三角形,
以及分别以它的每边为
一边向外所作的正方形.
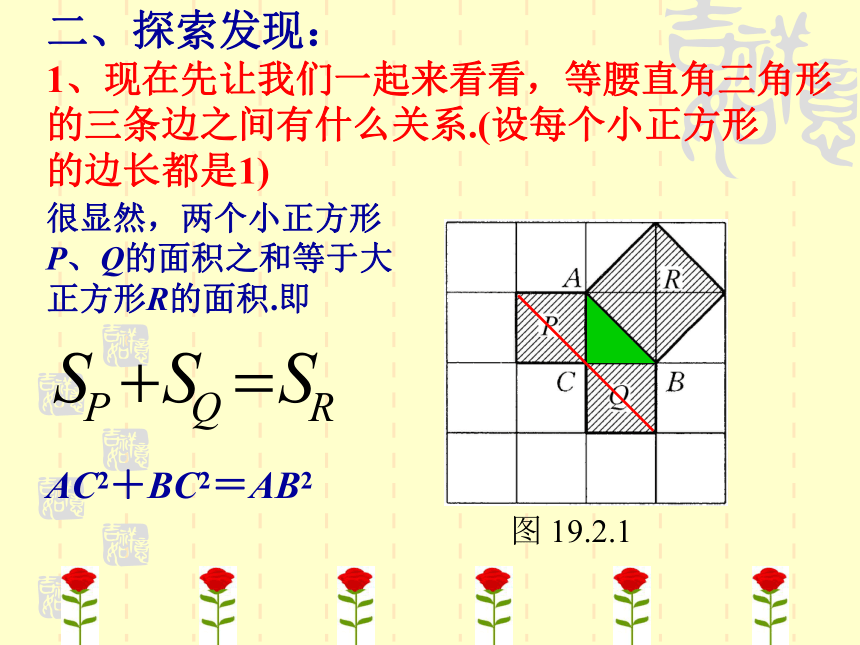
很显然,两个小正方形
P、Q的面积之和等于大
正方形R的面积.即
二、探索发现:
1、现在先让我们一起来看看,等腰直角三角形
的三条边之间有什么关系.(设每个小正方形
的边长都是1)
AC2+BC2=AB2
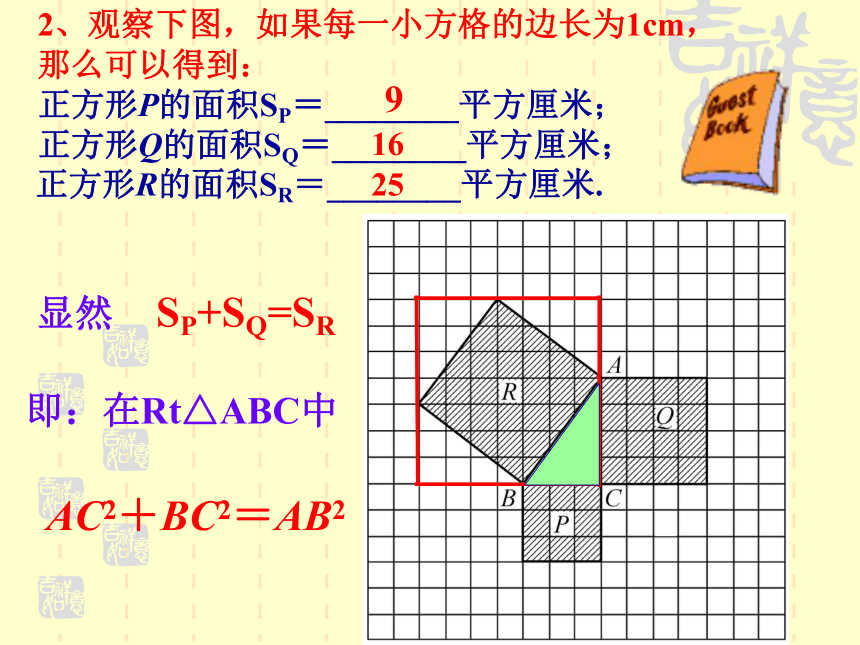
2、观察下图,如果每一小方格的边长为1cm,
那么可以得到:
正方形P的面积SP=________平方厘米;
正方形Q的面积SQ=________平方厘米;
正方形R的面积SR=________平方厘米.
显然 SP+SQ=SR即:在Rt△ABC中91625AC2+BC2=AB2
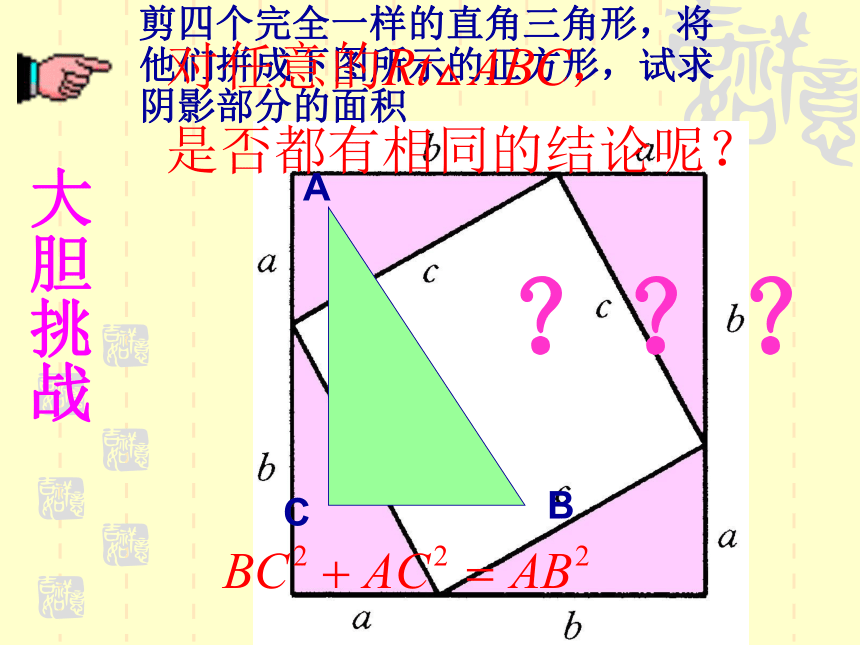
剪四个完全一样的直角三角形,将他们拼成下图所示的正方形,试求阴影部分的面积大胆挑战
???a2+b2=c2
三、勾股定理
勾股定理:直角三角形两
直角边的平方和等于斜边的平方.
注:
(1)勾股定理揭示了直角三角形三边之间的关系.
(2)在直角三角形中,任意已知其中的两边,就
可以计算出第三边的长例1.如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
EFGH四、现学现用:五、课堂练习课本102页 1、(1)
2、请大家认真答题? 例2、如图,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米) 解 在Rt△ABC中,
∠ABC=90゜,
BC=2.16, CA=5.41,
根据勾股定理得
≈4.96(米) 5.142.16谈谈这节课的收获勾股定理
直角三角形两直角边的
平方和等于斜边的平方.
a2+b2=c2
再见 勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之后。
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。读一读欣赏定理的证明方法一abcabc欣赏定理的证明方法二
奇异之树——勾股树这好像是一棵柏树呢!
如果在树上挂一串彩
色灯泡,再挂上些小
铃铛、小彩球、小礼
盒、小的圣诞老人,
就会成为一棵圣诞树.
可是,它与勾股有什么
关系呢?
可是,它与勾股有什么
关系呢?仔细看看,你
会发现,奥妙在树干和
树枝上,整棵树都是由
下图的这个基本图形组
成的:一个直角三角形,
以及分别以它的每边为
一边向外所作的正方形.
很显然,两个小正方形
P、Q的面积之和等于大
正方形R的面积.即
二、探索发现:
1、现在先让我们一起来看看,等腰直角三角形
的三条边之间有什么关系.(设每个小正方形
的边长都是1)
AC2+BC2=AB2
2、观察下图,如果每一小方格的边长为1cm,
那么可以得到:
正方形P的面积SP=________平方厘米;
正方形Q的面积SQ=________平方厘米;
正方形R的面积SR=________平方厘米.
显然 SP+SQ=SR即:在Rt△ABC中91625AC2+BC2=AB2
剪四个完全一样的直角三角形,将他们拼成下图所示的正方形,试求阴影部分的面积大胆挑战
???a2+b2=c2
三、勾股定理
勾股定理:直角三角形两
直角边的平方和等于斜边的平方.
注:
(1)勾股定理揭示了直角三角形三边之间的关系.
(2)在直角三角形中,任意已知其中的两边,就
可以计算出第三边的长例1.如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
EFGH四、现学现用:五、课堂练习课本102页 1、(1)
2、请大家认真答题? 例2、如图,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米) 解 在Rt△ABC中,
∠ABC=90゜,
BC=2.16, CA=5.41,
根据勾股定理得
≈4.96(米) 5.142.16谈谈这节课的收获勾股定理
直角三角形两直角边的
平方和等于斜边的平方.
a2+b2=c2
再见 勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之后。
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。读一读欣赏定理的证明方法一abcabc欣赏定理的证明方法二
