勾股定理[上学期]
图片预览




文档简介
课件17张PPT。第十九章
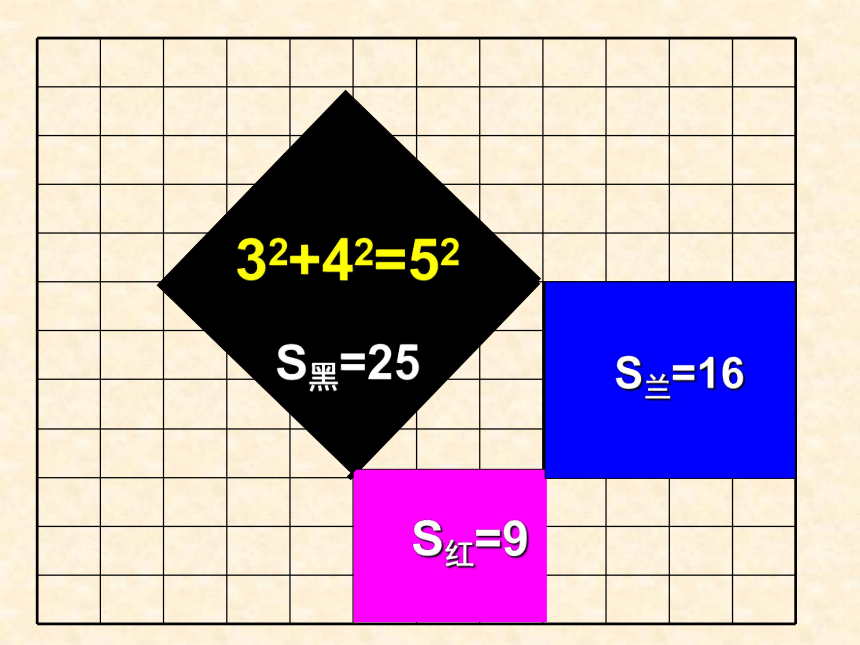
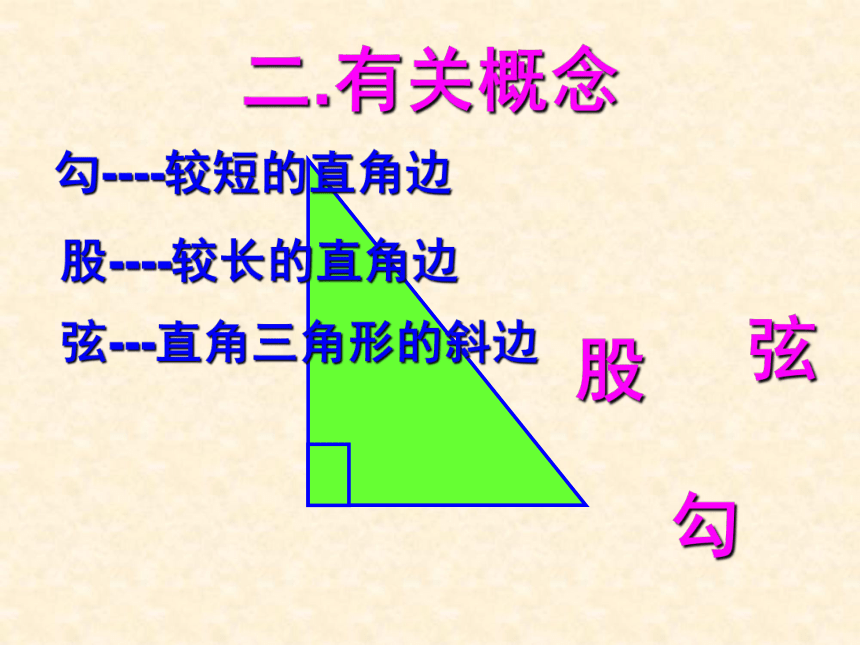
解直角三角形勾股定理一.练习引入在方格坐标纸上任画一个直角三角形 ABC (C为直角),再分别以三边a,b,c向外作正方形, 观察三个正方形面积间有何关系?S红=9S兰=16S黑=2532+42=5251213S红+S兰=S黑52+122=132两直角边的平方和等于斜边的平方.二.有关概念勾----较短的直角边股----较长的直角边弦---直角三角形的斜边勾股弦 勾股定理
任意直角三角形中,两直角边的平方和 等于斜边的平方.即若两直角边分别为 a, b,斜边为 c ,则
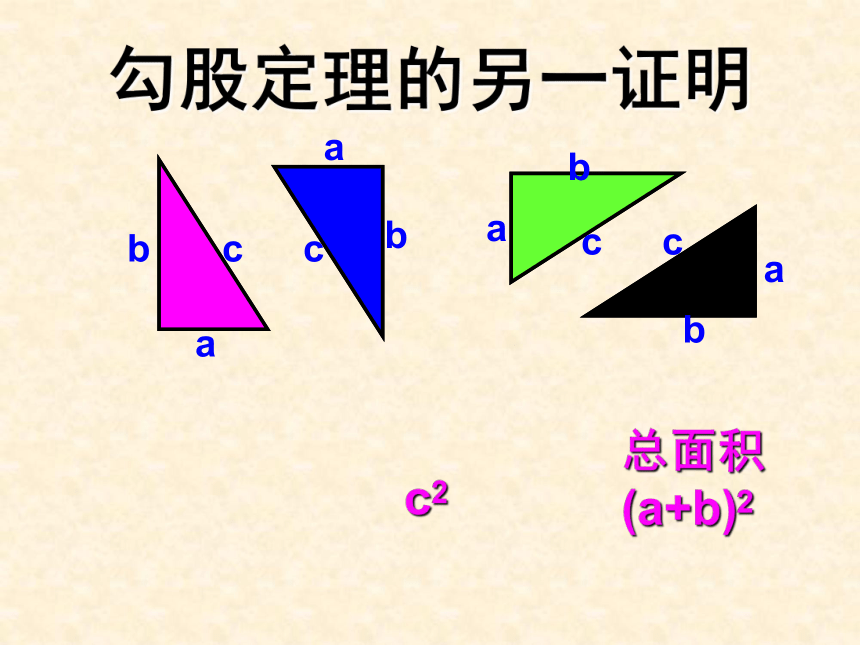
a2+b2=c2.勾股定理的另一证明baccababccba总面积(a+b)2c2由大正方形的面积等于四个直角三角形的
面积加上边长为c的小正方形的面积可得:例题讲练例1 已知Rt△ABC中,∠A=Rt∠,如图 (1)若a=15,b=12,求c
(2)若b=8, c=15,求acbaABC思维方式:A为直角,由勾股定理 得到a2=b2+c2.例题2如图在垂直于地面的墙上2m的A点斜放一个长为2.5m的梯子,由于不小心梯子在墙上下滑0.5米,求梯子在地面上滑出的距离BB?的长度.ABB?A?分析: 因直角三角形ABC中已知斜边AB和直角边AC的长由勾股定理可得边BC的长.又由AA?=0.5, A?B?=AB,再次运用勾股定理可求B?C? 的长,从而求得B?B的长.ABB?A?C基础练习教材P104练习T1,2.思考题 现有两根木棒,其长度分别为 50cm和40cm。要钉成一个三角形木架,其中有一个角为直角,求所需木棒的最短长度。答案:30cm小 结1.利用数学模型验证和探索勾股定理的正确性,勾股定理在日常生活中应用非常广泛;
2.勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.即若两直角边分别为 a, b,斜边为c 则 a2+b2=c2.作业 教材P104习题19.2.
(2)若b=8, c=15,求acbaABC思维方式:A为直角,由勾股定理 得到a2=b2+c2.例题2如图在垂直于地面的墙上2m的A点斜放一个长为2.5m的梯子,由于不小心梯子在墙上下滑0.5米,求梯子在地面上滑出的距离BB?的长度.ABB?A?分析: 因直角三角形ABC中已知斜边AB和直角边AC的长由勾股定理可得边BC的长.又由AA?=0.5, A?B?=AB,再次运用勾股定理可求B?C? 的长,从而求得B?B的长.ABB?A?C基础练习教材P104练习T1,2.思考题 现有两根木棒,其长度分别为 50cm和40cm。要钉成一个三角形木架,其中有一个角为直角,求所需木棒的最短长度。答案:30cm小 结1.利用数学模型验证和探索勾股定理的正确性,勾股定理在日常生活中应用非常广泛;
2.勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.即若两直角边分别为 a, b,斜边为c 则 a2+b2=c2.作业 教材P104习题19.2.
