人教版八年级下册18.2.1矩形巩固练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.1矩形巩固练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 397.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 10:31:15 | ||
图片预览



文档简介
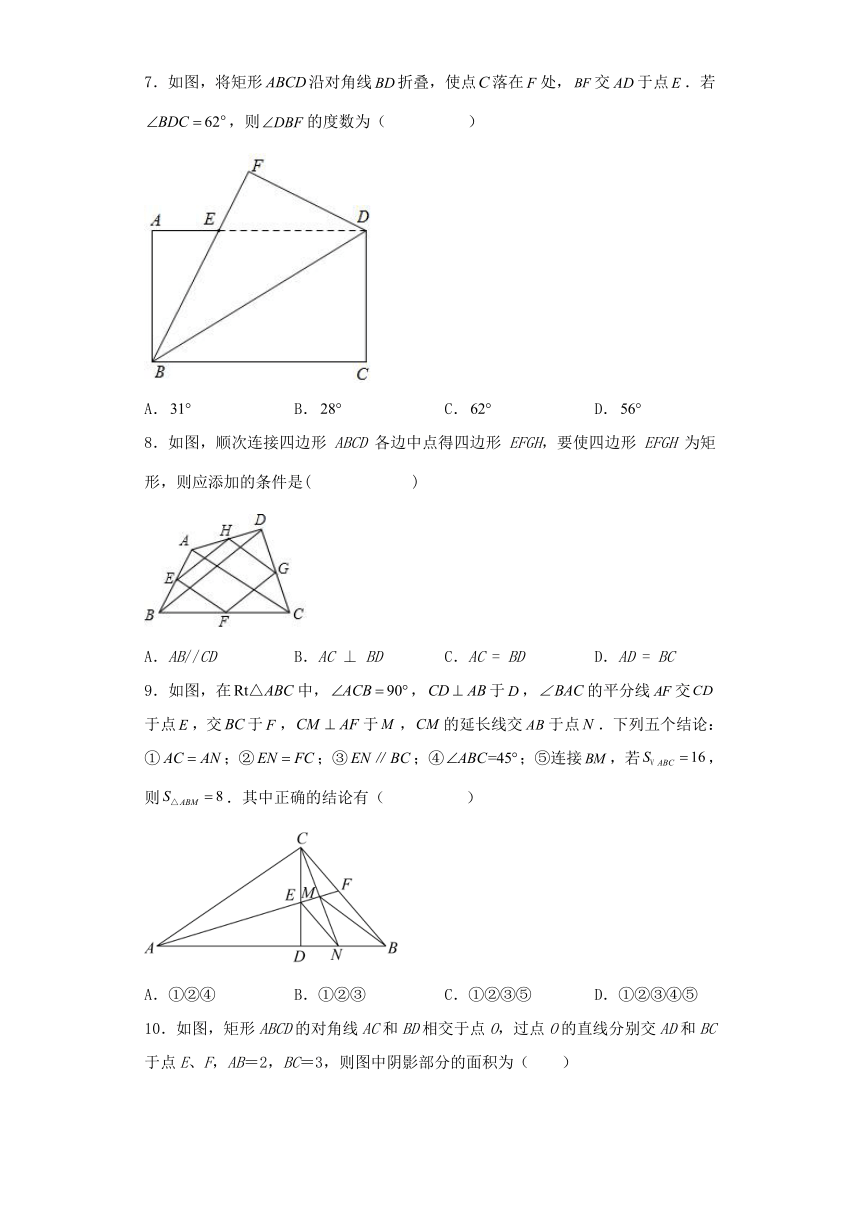
18.2.1矩形 巩固练习
一、单选题
1.已知矩形ABCD的周长为16,AB=5,则BC等于( )
A.3 B.5 C.6 D.11
2.如图,将平行四边形的变成直角,则平行四边形变成( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.长方形的一条对角线的长为,一边长为,它的面积是( )
A. B. C. D.
4.长方形的一边长为4,对角线与长方形另外一条边相差2,则长方形的面积为( )
A.8 B.4 C.6 D.12
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=8,则EC的长度为( )
A.2 B.2 C.4 D.
6.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
7.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
8.如图,顺次连接四边形 ABCD 各边中点得四边形 EFGH,要使四边形 EFGH 为矩形,则应添加的条件是( )
A.AB//CD B.AC ⊥ BD C.AC = BD D.AD = BC
9.如图,在中,,于,的平分线交于点,交于,于,的延长线交于点.下列五个结论:①;②;③;④;⑤连接,若,则.其中正确的结论有( )
A.①②④ B.①②③ C.①②③⑤ D.①②③④⑤
10.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A.3 B.4 C.5 D.6
二、填空题
11.在矩形中,作的平分线交直线于点E,则是____________度.
12.如图,已知矩形的对角线与相交于点,若,那么______.
13.将一个矩形纸片按如图所示折叠,若, 则的度数是______.
14.如图,在矩形ABCD中,,,P是AD边上一点,BP平分,则△DBP的面积是______.
15.如图,在△ ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DEAB交AE于E,则四边形ADCE的形状是___________
三、解答题
16.如图,在□ABCD中,点E在AD上,以BE为折痕将△ABE翻折,点A恰好落在CD边上的点F处. 已知△EDF的周长为12,△BCF的周长为22,求CF的长.
17.已知矩形ABCD中,AD=+,AB=-,求这个矩形的对角线AC的长及其面积.
18.已知,如图长方形中,,,将此长方形折叠,使点B与点D重合,折痕为,求的长.
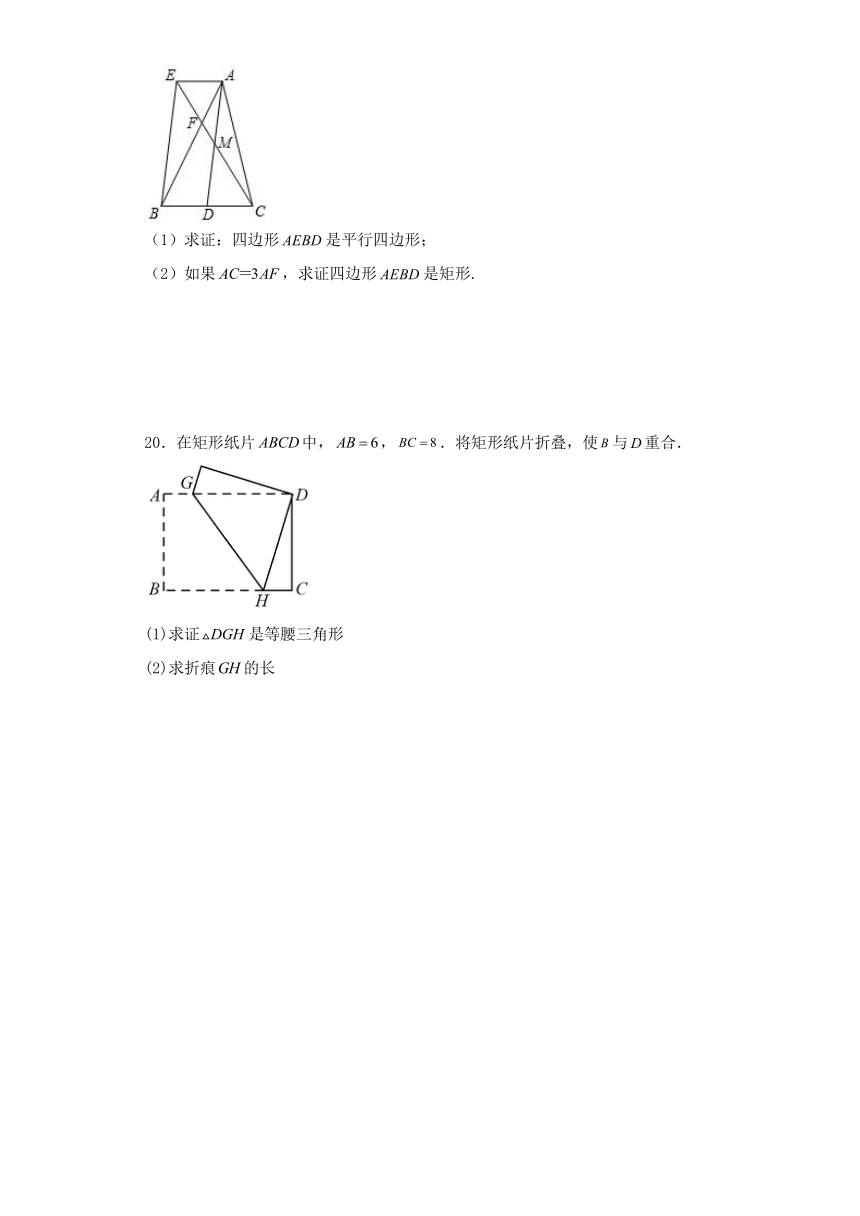
19.如图,已知AD是的中线,M是AD的中点,过A点作,CM的延长线与AE相交于点E,与AB相交于点F.
(1)求证:四边形是平行四边形;
(2)如果,求证四边形是矩形.
20.在矩形纸片中,,.将矩形纸片折叠,使与重合.
(1)求证是等腰三角形
(2)求折痕的长
参考答案
1.A
2.B
3.D
4.D
5.B
6.B
7.B
8.B
9.C
10.A
11.45或135
12.2
13.40°
14.3.75
15.矩形
16.如图,∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC;
由题意得:AE=EF,AB=BF;
∵△FDE的周长为12,△FCB的周长为22,∴DE+DF+EF=12,CF+BC+BF=22,
∴(DE+EA)+(DF+CF)+BC+AB=34,即2(AB+BC)=34,
∴AB+BC=17,即BF+BC=17,
∴FC=22-17=5.
故答案为FC=5.
17.解:,
∴,
∴矩形的面积.
18.解:过点E做于点H,
过点E作
∵四边形是长方形
四边形是矩形
设,
由折叠知,
,
在中,
解得,
,
,
又,
,
,
又,
,
在中,
19.证明:(1)是的中点,
,
,
,
又,
,
,
又是的中线,
,
又,
四边形是平行四边形;
(2),
,
∴,即,
,
又,
,
又是的中线,
,
又四边形是平行四边形,
四边形是矩形.
20.(1)如图,矩形纸片折叠后,设与重合,过点G作于点E,
由折叠的性质得:
,,,,
四边形是矩形,
,,, ,
,
,
,
是等腰三角形.
(2),
,
, ,
,,
设,则,由勾股定理得:
,
解得:,
,
,
在中,由勾股定理得:
,
.
一、单选题
1.已知矩形ABCD的周长为16,AB=5,则BC等于( )
A.3 B.5 C.6 D.11
2.如图,将平行四边形的变成直角,则平行四边形变成( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3.长方形的一条对角线的长为,一边长为,它的面积是( )
A. B. C. D.
4.长方形的一边长为4,对角线与长方形另外一条边相差2,则长方形的面积为( )
A.8 B.4 C.6 D.12
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=8,则EC的长度为( )
A.2 B.2 C.4 D.
6.如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E,,则的度数为( )
A.40° B.35° C.30° D.25°
7.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
8.如图,顺次连接四边形 ABCD 各边中点得四边形 EFGH,要使四边形 EFGH 为矩形,则应添加的条件是( )
A.AB//CD B.AC ⊥ BD C.AC = BD D.AD = BC
9.如图,在中,,于,的平分线交于点,交于,于,的延长线交于点.下列五个结论:①;②;③;④;⑤连接,若,则.其中正确的结论有( )
A.①②④ B.①②③ C.①②③⑤ D.①②③④⑤
10.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
A.3 B.4 C.5 D.6
二、填空题
11.在矩形中,作的平分线交直线于点E,则是____________度.
12.如图,已知矩形的对角线与相交于点,若,那么______.
13.将一个矩形纸片按如图所示折叠,若, 则的度数是______.
14.如图,在矩形ABCD中,,,P是AD边上一点,BP平分,则△DBP的面积是______.
15.如图,在△ ABC,AB=AC,点D为BC的中点,AE是∠BAC外角的平分线,DEAB交AE于E,则四边形ADCE的形状是___________
三、解答题
16.如图,在□ABCD中,点E在AD上,以BE为折痕将△ABE翻折,点A恰好落在CD边上的点F处. 已知△EDF的周长为12,△BCF的周长为22,求CF的长.
17.已知矩形ABCD中,AD=+,AB=-,求这个矩形的对角线AC的长及其面积.
18.已知,如图长方形中,,,将此长方形折叠,使点B与点D重合,折痕为,求的长.
19.如图,已知AD是的中线,M是AD的中点,过A点作,CM的延长线与AE相交于点E,与AB相交于点F.
(1)求证:四边形是平行四边形;
(2)如果,求证四边形是矩形.
20.在矩形纸片中,,.将矩形纸片折叠,使与重合.
(1)求证是等腰三角形
(2)求折痕的长
参考答案
1.A
2.B
3.D
4.D
5.B
6.B
7.B
8.B
9.C
10.A
11.45或135
12.2
13.40°
14.3.75
15.矩形
16.如图,∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC;
由题意得:AE=EF,AB=BF;
∵△FDE的周长为12,△FCB的周长为22,∴DE+DF+EF=12,CF+BC+BF=22,
∴(DE+EA)+(DF+CF)+BC+AB=34,即2(AB+BC)=34,
∴AB+BC=17,即BF+BC=17,
∴FC=22-17=5.
故答案为FC=5.
17.解:,
∴,
∴矩形的面积.
18.解:过点E做于点H,
过点E作
∵四边形是长方形
四边形是矩形
设,
由折叠知,
,
在中,
解得,
,
,
又,
,
,
又,
,
在中,
19.证明:(1)是的中点,
,
,
,
又,
,
,
又是的中线,
,
又,
四边形是平行四边形;
(2),
,
∴,即,
,
又,
,
又是的中线,
,
又四边形是平行四边形,
四边形是矩形.
20.(1)如图,矩形纸片折叠后,设与重合,过点G作于点E,
由折叠的性质得:
,,,,
四边形是矩形,
,,, ,
,
,
,
是等腰三角形.
(2),
,
, ,
,,
设,则,由勾股定理得:
,
解得:,
,
,
在中,由勾股定理得:
,
.
