14.2勾股定理[上学期]
图片预览
文档简介
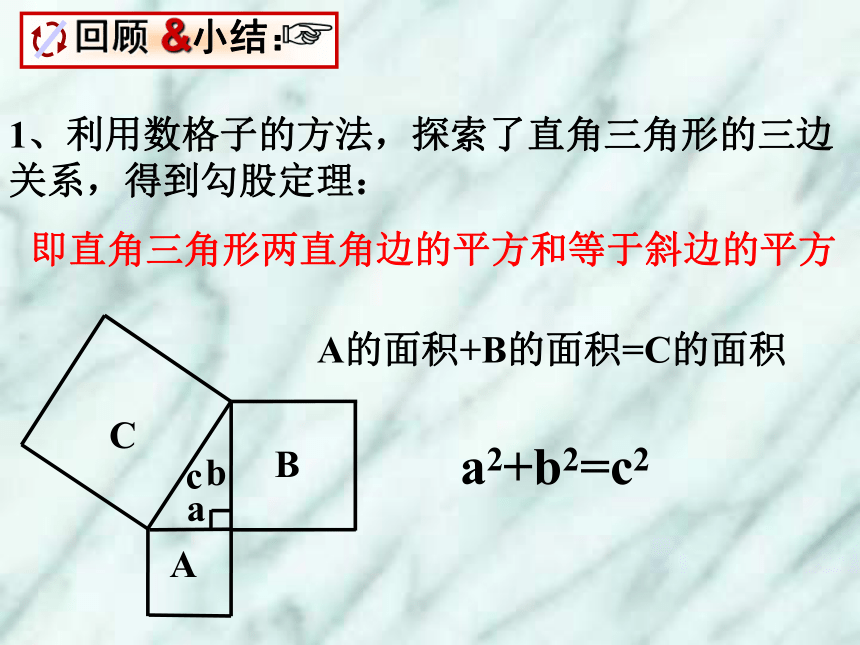
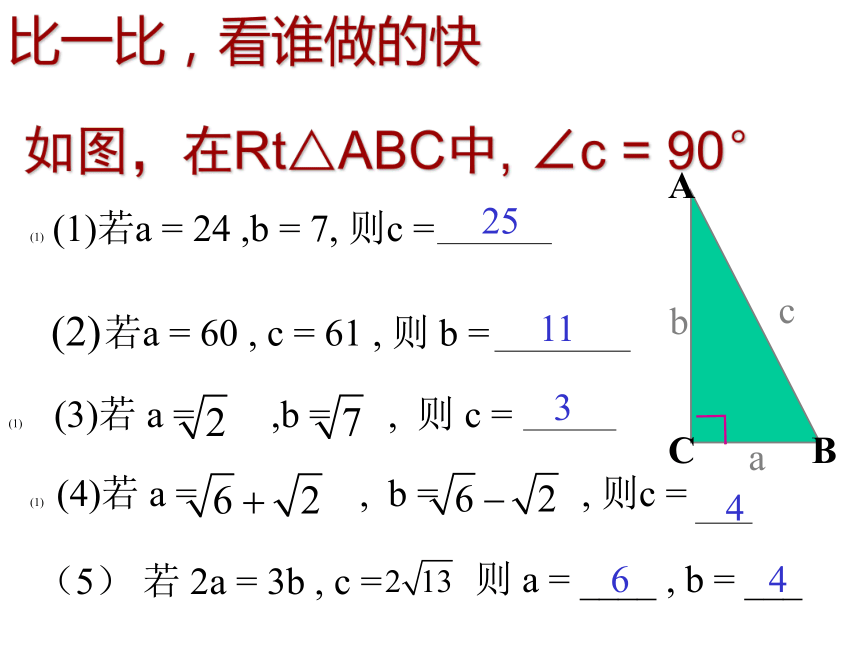
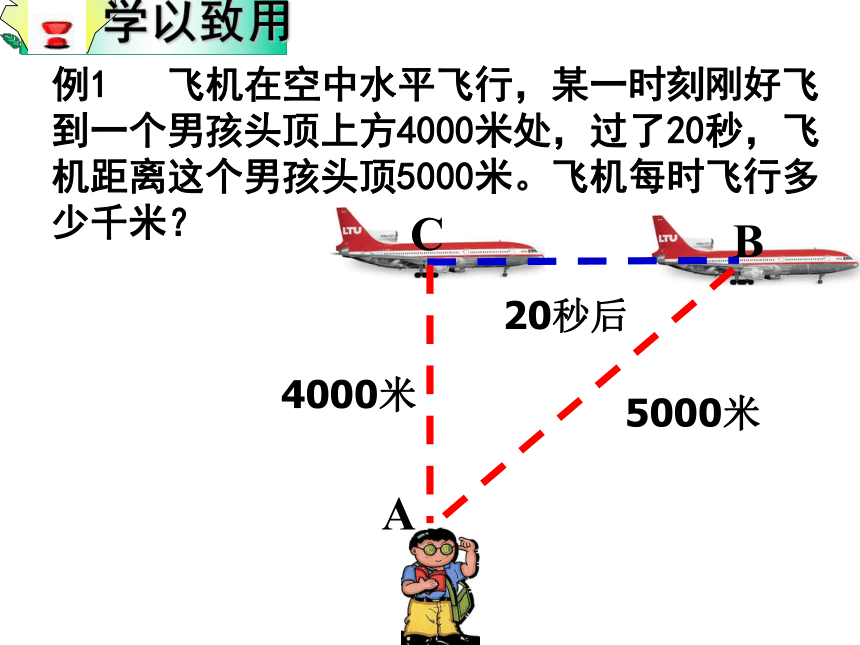
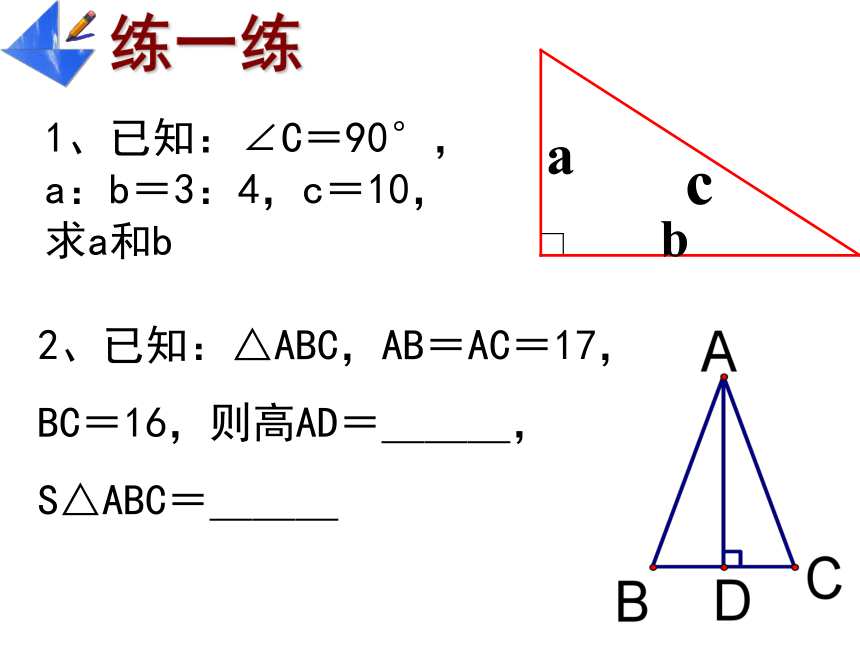
课件14张PPT。18.1.2勾股定理21、利用数格子的方法,探索了直角三角形的三边关系,得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方A的面积+B的面积=C的面积a2+b2=c2比一比,看谁做的快 32511464如图,在Rt△ABC中, ∠c = 90°例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?A4000米5000米20秒后BC1、已知:∠C=90°,a:b=3:4,c=10,求a和b2、已知:△ABC,AB=AC=17,
BC=16,则高AD=___,
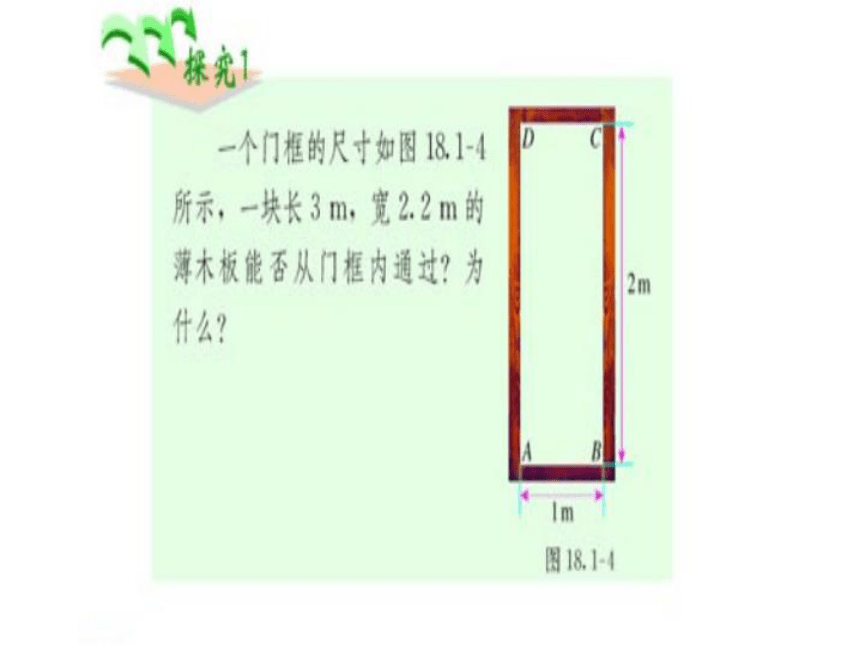
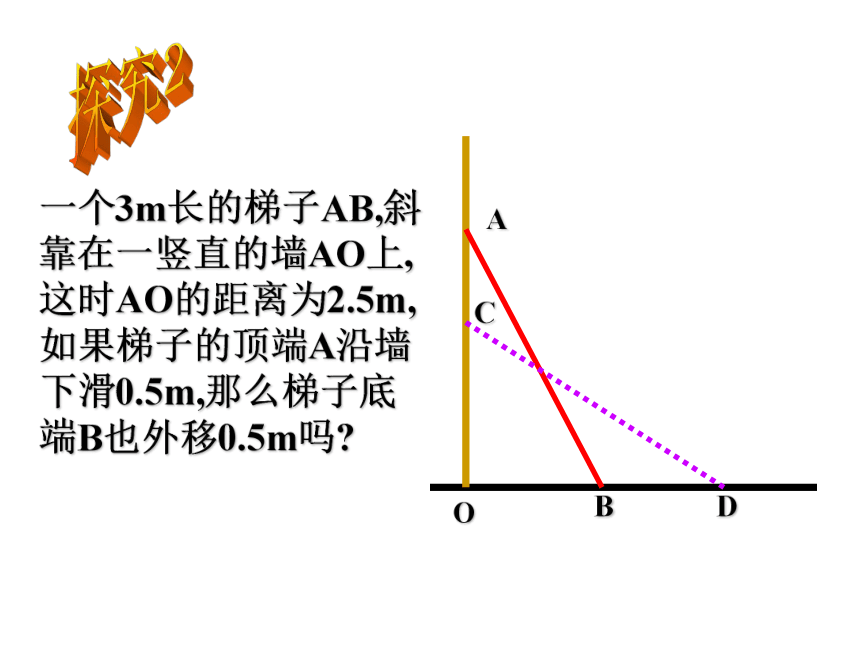
S△ABC=___探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米; CDDA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE1、已知:a=3,
b=4,求c2、已知: c =10,a=6,求b例2:在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积。ABCD131310H提示:利用面积相等的关系课堂小结⒈ 勾股定理是几何中最重要的定理之一,它揭示了直
角三角形三边之间的数量关系.⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1,则a,b,c为
基本勾股数.如:3、4、5 ; 5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、15……
3、一组勾股数中必有一个数是5倍数
BC=16,则高AD=___,
S△ABC=___探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米; CDDA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE1、已知:a=3,
b=4,求c2、已知: c =10,a=6,求b例2:在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积。ABCD131310H提示:利用面积相等的关系课堂小结⒈ 勾股定理是几何中最重要的定理之一,它揭示了直
角三角形三边之间的数量关系.⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1,则a,b,c为
基本勾股数.如:3、4、5 ; 5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、15……
3、一组勾股数中必有一个数是5倍数
