14.2勾股定理应用[上学期]
图片预览






文档简介
课件20张PPT。§19.2 勾股定理(一) 上虞龙浦中学 乔哥哥 八年级数学(下册)? 华师大版弦图 这个图形里 到底蕴涵了什么样博大精深的知识呢?
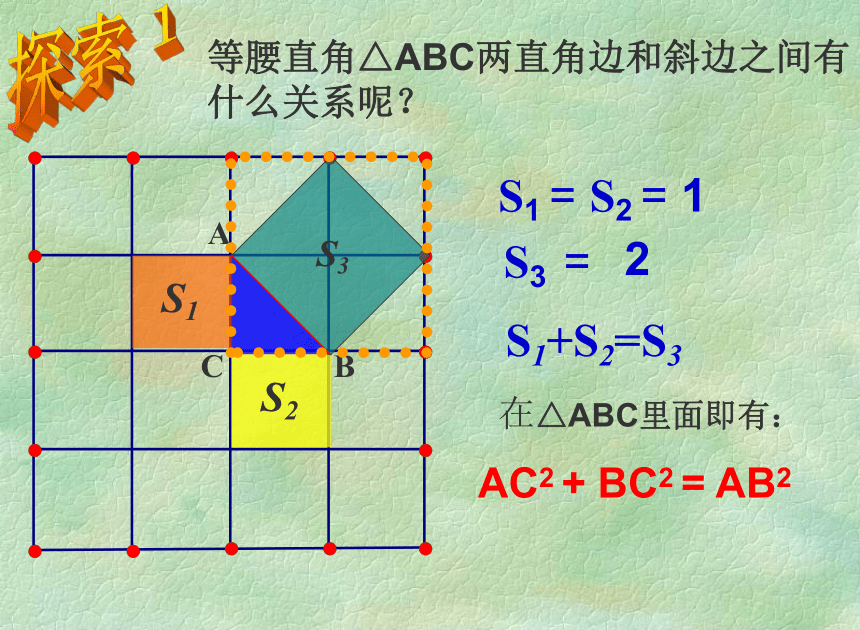
它标志着我国古代数学的成就! S2 S1S3等腰直角△ABC两直角边和斜边之间有什么关系呢?探索1S1+S2=S3
在△ABC里面即有:AC2 + BC2 = AB2S1 = S2 = 1 S3 =2
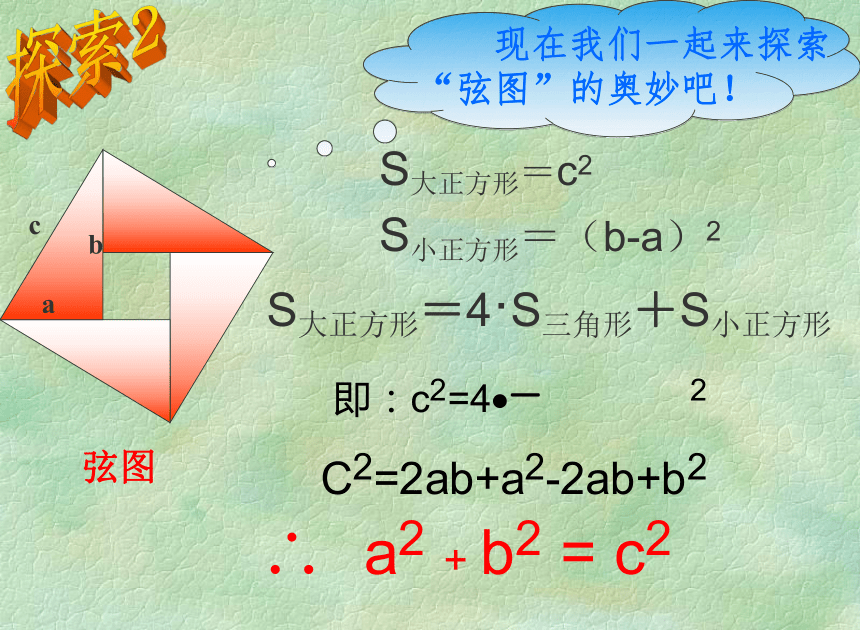
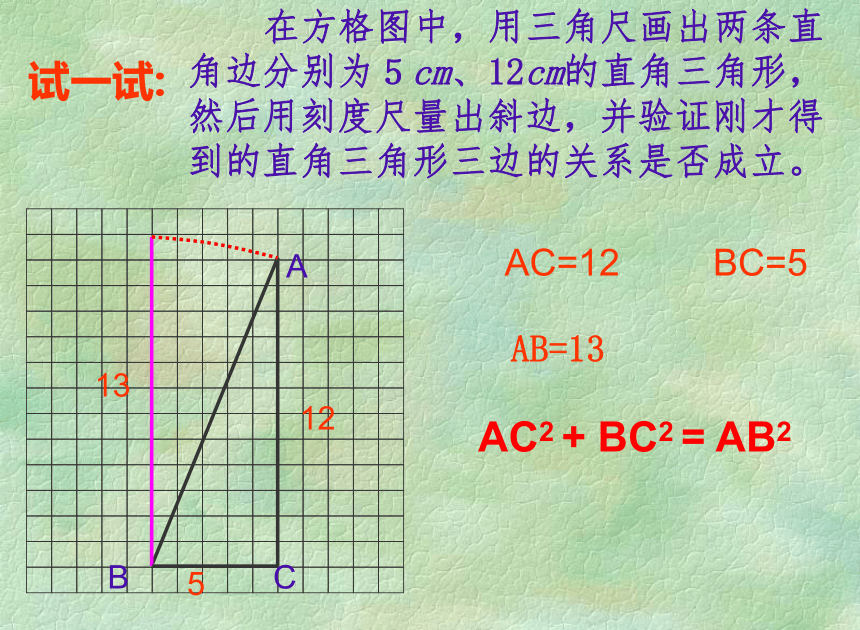
abcS大正方形=c2S小正方形=(b-a)2探索2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧! 在方格图中,用三角尺画出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边,并验证刚才得到的直角三角形三边的关系是否成立。试一试:12135ABCAC=12 BC=5AC2 + BC2 = AB2AB=13总结规律 对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有 a2 + b2 = c2 , 直角三角形两直角边的平方和等于斜边的平方。 这种关系我们称为勾股定理。注意:勾股定理只适用在直角三角形中求边之间的关系!勾股史话 商高定理:
商高是公元前 十一世纪的中国人。当时中国的朝代是西周, 是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。 商高定理就是勾股定理哦!毕达哥拉斯定理: 毕达哥拉斯 “勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.
相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”. 毕达哥拉斯(Pythagoras,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2比一比,看谁做得快如图,在Rt△ABC中, ∠C = 90°,381364abc解:C=4 或 C=-4(舍去)1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2. ( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××能力比拼1、例题:将长为5.41米的梯子AC斜靠
在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米)实际应用解:在Rt△ABC中,∠ABC=90°
BC=2.16; CA=5.41,根据勾股定理得:≈4.96(米)答:梯子上端A到墙的底端B的距离为4.96米。能力升级1、如图,已知?ABC中,AB=AC=3,BC=2,求?ABC的面积.D解:作AD⊥BC,垂足分别为D, × ×根据等腰三角形“三线合一”的性质:
BD=1,AB=3,
∴小结:1、通过用格点三角形及“弦图”的方式探索直角三角形两直角边与斜边之间的关系。2、得到直角三角形两直角边与斜边之间的关系——勾股定理:直角三角形两直角边的平方和等于斜边的平方。3、练习的使用了勾股定理来解决直角三角形里的一些问题。 这些内容你都掌握清楚了吗? 想一想:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”“平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长。根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt△ABC中,∠BAC = 90o ,所以有:( x + 0.5 )2 = x2 + 22求:AB的长。谢 谢 !
它标志着我国古代数学的成就! S2 S1S3等腰直角△ABC两直角边和斜边之间有什么关系呢?探索1S1+S2=S3
在△ABC里面即有:AC2 + BC2 = AB2S1 = S2 = 1 S3 =2
abcS大正方形=c2S小正方形=(b-a)2探索2S大正方形=4·S三角形+S小正方形弦图 现在我们一起来探索“弦图”的奥妙吧! 在方格图中,用三角尺画出两条直角边分别为5cm、12cm的直角三角形,然后用刻度尺量出斜边,并验证刚才得到的直角三角形三边的关系是否成立。试一试:12135ABCAC=12 BC=5AC2 + BC2 = AB2AB=13总结规律 对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有 a2 + b2 = c2 , 直角三角形两直角边的平方和等于斜边的平方。 这种关系我们称为勾股定理。注意:勾股定理只适用在直角三角形中求边之间的关系!勾股史话 商高定理:
商高是公元前 十一世纪的中国人。当时中国的朝代是西周, 是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作 “商高定理”。 商高定理就是勾股定理哦!毕达哥拉斯定理: 毕达哥拉斯 “勾股定理”在国外,尤其在西方被称为“毕达哥拉斯定理”或“百牛定理”.
相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理又叫做“百牛定理”. 毕达哥拉斯(Pythagoras,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。cba公式变形c2=a2 + b2a2=c2-b2b2 =c2-a2比一比,看谁做得快如图,在Rt△ABC中, ∠C = 90°,381364abc解:C=4 或 C=-4(舍去)1、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2. ( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××能力比拼1、例题:将长为5.41米的梯子AC斜靠
在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米)实际应用解:在Rt△ABC中,∠ABC=90°
BC=2.16; CA=5.41,根据勾股定理得:≈4.96(米)答:梯子上端A到墙的底端B的距离为4.96米。能力升级1、如图,已知?ABC中,AB=AC=3,BC=2,求?ABC的面积.D解:作AD⊥BC,垂足分别为D, × ×根据等腰三角形“三线合一”的性质:
BD=1,AB=3,
∴小结:1、通过用格点三角形及“弦图”的方式探索直角三角形两直角边与斜边之间的关系。2、得到直角三角形两直角边与斜边之间的关系——勾股定理:直角三角形两直角边的平方和等于斜边的平方。3、练习的使用了勾股定理来解决直角三角形里的一些问题。 这些内容你都掌握清楚了吗? 想一想:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”“平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长。根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt△ABC中,∠BAC = 90o ,所以有:( x + 0.5 )2 = x2 + 22求:AB的长。谢 谢 !
