人教版九年级下册28.2.1解直角三角形 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级下册28.2.1解直角三角形 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 590.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 11:14:30 | ||
图片预览


文档简介
(共17张PPT)
人民教育出版社 九年级下册
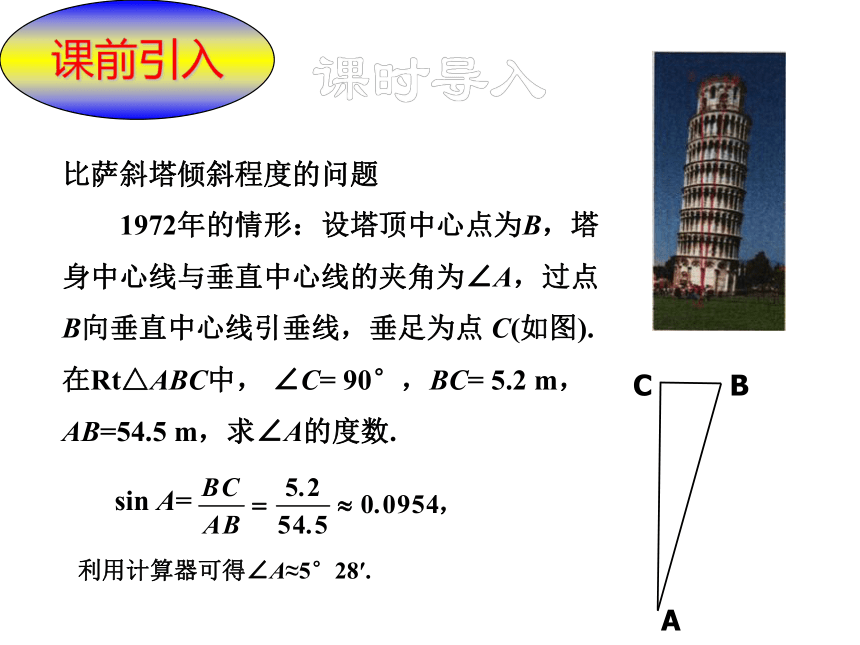
1972年的情形:设塔顶中心点为B,塔
身中心线与垂直中心线的夹角为∠A,过点
B向垂直中心线引垂线,垂足为点 C(如图).
在Rt△ABC中, ∠C= 90°,BC= 5.2 m,
AB=54.5 m,求∠A的度数.
比萨斜塔倾斜程度的问题
课前引入
C
B
A
sin A=
利用计算器可得∠A≈5°28′.
初步体验
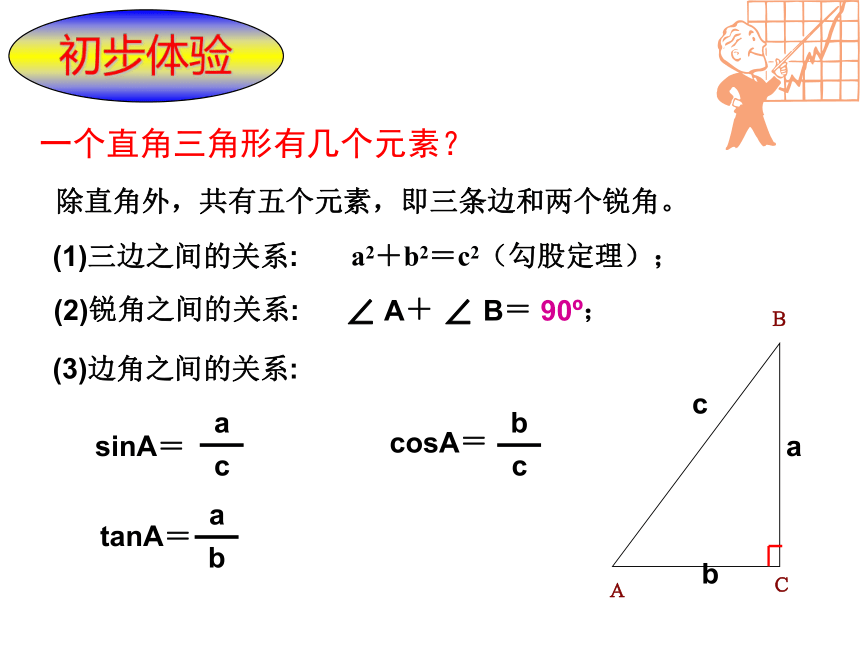
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
除直角外,共有五个元素,即三条边和两个锐角。
b
c
a
b
一个直角三角形有几个元素?
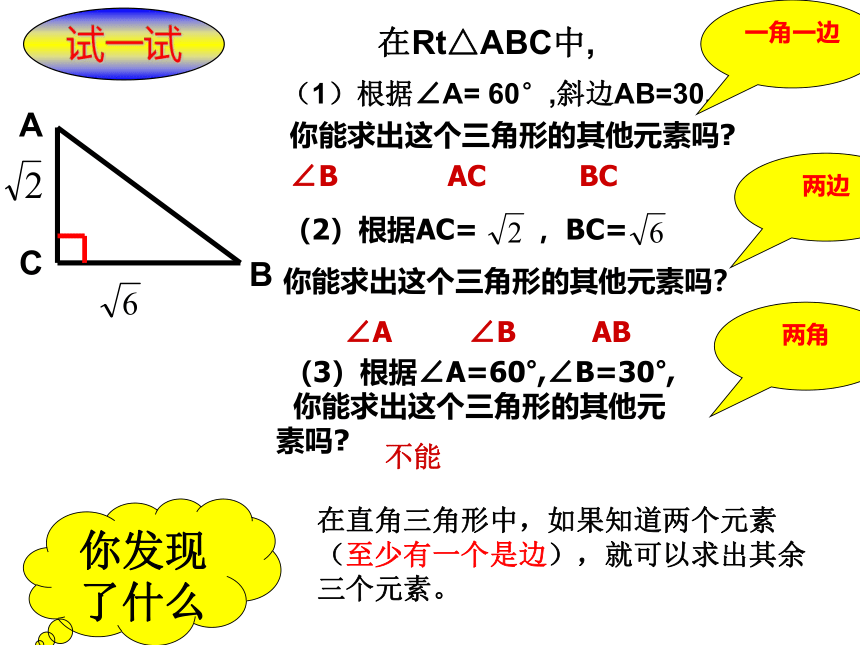
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
在直角三角形中,如果知道两个元素(至少有一个是边),就可以求出其余三个元素。
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
不能
你能求出这个三角形的其他元素吗
试一试
例:在Rt△ABC中,∠C=90°,∠B=35°,b=20,
解这个直角三角形. (精确到0.1)
A
C
B
a
b
c
参考值
tan35°≈0.70
sin35° ≈0.57
cos35°≈0.82
例题解析
解:
∵
35°
20
?
?
?
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形
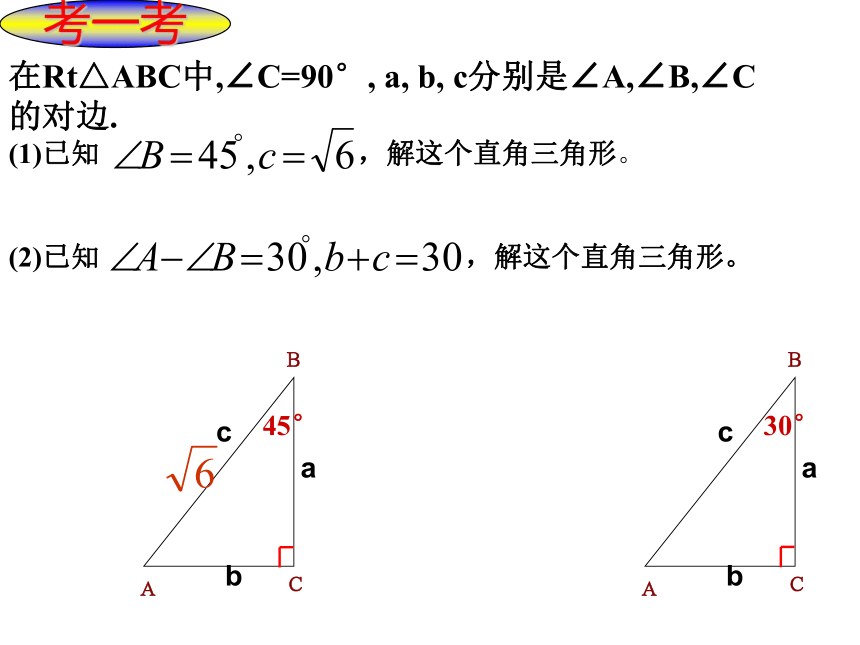
在Rt△ABC中,∠C=90°, a, b, c分别是∠A,∠B,∠C的对边.
(1)已知 ,解这个直角三角形。
(2)已知 ,解这个直角三角形。
A
C
B
a
b
c
A
C
B
a
b
c
45°
30°
考一考
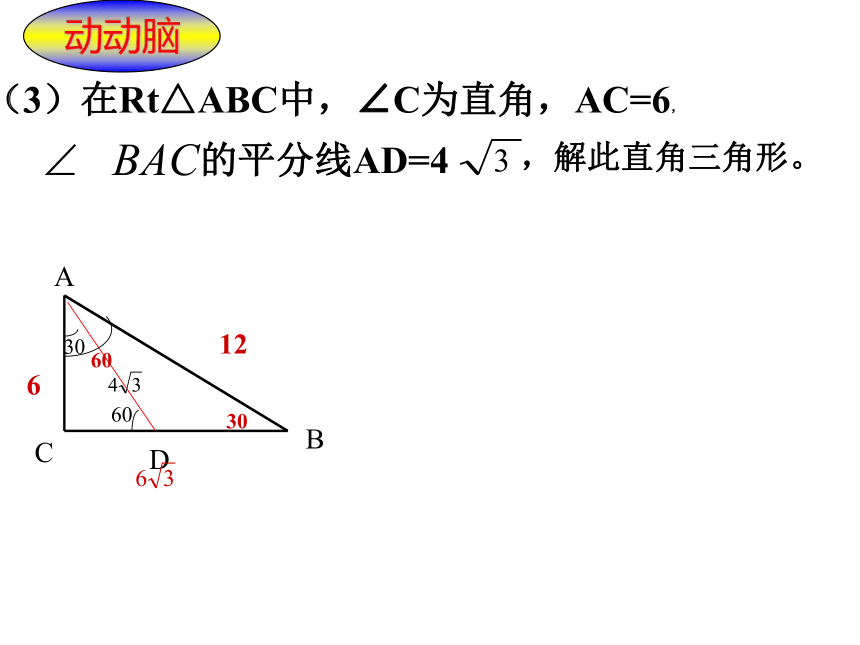
的平分线AD=4
(3)在Rt△ABC中,∠C为直角,AC=6,
,解此直角三角形。
A
D
B
C
动动脑
30
60
60
30
6
12
动动脑
(4)如图在△ABC中,∠C=90°,
拓展提高
1. 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积。
A
B
C
450
300
4cm
2. 在四边形ABCD中,∠ A= ,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD,BC的长(保留根号)?
60°
拓展提高
E
B
A
C
D
20
10
60°
30°
图①
3 在△ABC中,AB= ,AC=13,cos∠B= ,求BC的长.
解:∵cos∠B = ,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC=13,∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7;
图②
当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.
∴ BC的长为7或17.
课堂总结
谈谈你的收获!
直击中考
图1是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算: 如图2,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10cm,DE=120cm,FG⊥DE,垂足为点G.
(1)若∠θ=37°50′,则AB的长约为 cm;
(参考数据:sin37°50′≈0.61,cos37°50′≈0.79,tan37°50′≈0.78)
(2)若FG=30cm,∠θ=60°,求CF的长.
1、作业本2 第23页;
2、巧学巧练A 第90页。
作业
悟性的高低取决于有无悟“心”, 其实,人与人的差别就在于你是否去思考 ,去发现,去总结。
寄语
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据
A
C
B
a
b
c
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
归纳
人民教育出版社 九年级下册
1972年的情形:设塔顶中心点为B,塔
身中心线与垂直中心线的夹角为∠A,过点
B向垂直中心线引垂线,垂足为点 C(如图).
在Rt△ABC中, ∠C= 90°,BC= 5.2 m,
AB=54.5 m,求∠A的度数.
比萨斜塔倾斜程度的问题
课前引入
C
B
A
sin A=
利用计算器可得∠A≈5°28′.
初步体验
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
sinA=
a
c
cosA=
tanA=
A
C
B
a
b
c
除直角外,共有五个元素,即三条边和两个锐角。
b
c
a
b
一个直角三角形有几个元素?
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
在直角三角形中,如果知道两个元素(至少有一个是边),就可以求出其余三个元素。
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
(2)根据AC= ,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根据∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗
不能
你能求出这个三角形的其他元素吗
试一试
例:在Rt△ABC中,∠C=90°,∠B=35°,b=20,
解这个直角三角形. (精确到0.1)
A
C
B
a
b
c
参考值
tan35°≈0.70
sin35° ≈0.57
cos35°≈0.82
例题解析
解:
∵
35°
20
?
?
?
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形
在Rt△ABC中,∠C=90°, a, b, c分别是∠A,∠B,∠C的对边.
(1)已知 ,解这个直角三角形。
(2)已知 ,解这个直角三角形。
A
C
B
a
b
c
A
C
B
a
b
c
45°
30°
考一考
的平分线AD=4
(3)在Rt△ABC中,∠C为直角,AC=6,
,解此直角三角形。
A
D
B
C
动动脑
30
60
60
30
6
12
动动脑
(4)如图在△ABC中,∠C=90°,
拓展提高
1. 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积。
A
B
C
450
300
4cm
2. 在四边形ABCD中,∠ A= ,AB⊥BC,AD⊥DC,AB=20cm,CD=10cm,求AD,BC的长(保留根号)?
60°
拓展提高
E
B
A
C
D
20
10
60°
30°
图①
3 在△ABC中,AB= ,AC=13,cos∠B= ,求BC的长.
解:∵cos∠B = ,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC=13,∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7;
图②
当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.
∴ BC的长为7或17.
课堂总结
谈谈你的收获!
直击中考
图1是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算: 如图2,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10cm,DE=120cm,FG⊥DE,垂足为点G.
(1)若∠θ=37°50′,则AB的长约为 cm;
(参考数据:sin37°50′≈0.61,cos37°50′≈0.79,tan37°50′≈0.78)
(2)若FG=30cm,∠θ=60°,求CF的长.
1、作业本2 第23页;
2、巧学巧练A 第90页。
作业
悟性的高低取决于有无悟“心”, 其实,人与人的差别就在于你是否去思考 ,去发现,去总结。
寄语
在直角三角形中,由已知元素求未知元素的过程,叫
解直角三角形
解直角三角形的依据
A
C
B
a
b
c
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
归纳
