2022-2023学年北师大版八年级数学下册 3.2图形的旋转培优练习 (无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册 3.2图形的旋转培优练习 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 15:34:42 | ||
图片预览


文档简介
3.2 图形的旋转 培优练习
一.选择题
1.如图,已知△ABC中,∠C=90°
置,连接C'C,则∠C'CB的度数为( )
A.15° B.20° C.30° D.45°
2. 下列图形中,既是轴对称图形又是旋转对称图形的是
A. B.
C. D.
3.如图,在△ABC中,AC=18,得到△A′B′C,则下列说法错误的是( )
A.的长为5π B.A′C=18
C.∠BCA′=50° D.∠ACB=∠A′CB′
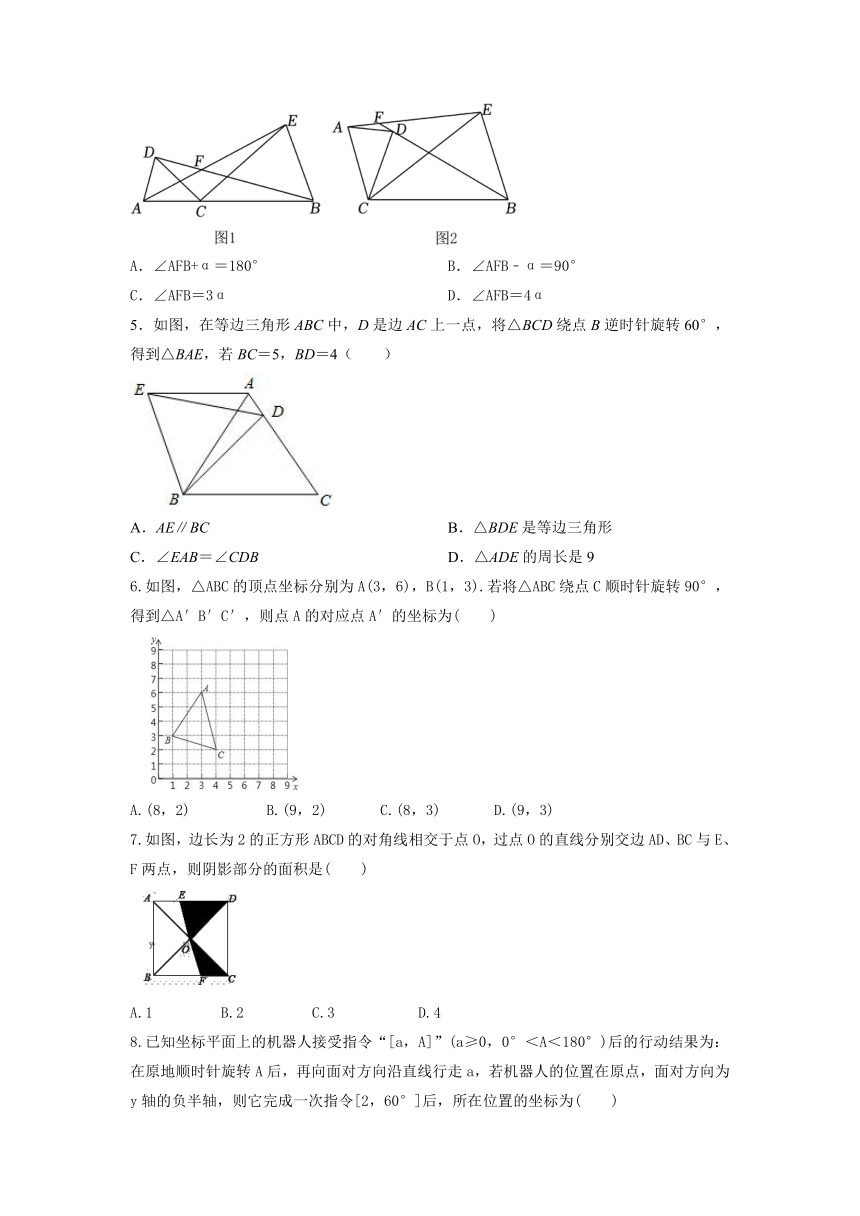
4.已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,∠ACD=∠BCE=α,直线AE与BD交于点F(交点F至少在BD、AE中的一条线段上),如图2,则∠AFB与α的数量关系为( )
A.∠AFB+α=180° B.∠AFB﹣α=90°
C.∠AFB=3α D.∠AFB=4α
5.如图,在等边三角形ABC中,D是边AC上一点,将△BCD绕点B逆时针旋转60°,得到△BAE,若BC=5,BD=4( )
A.AE∥BC B.△BDE是等边三角形
C.∠EAB=∠CDB D.△ADE的周长是9
6.如图,△ABC的顶点坐标分别为A(3,6),B(1,3).若将△ABC绕点C顺时针旋转90°,得到△A′B′C′,则点A的对应点A′的坐标为( )
A.(8,2) B.(9,2) C.(8,3) D.(9,3)
7.如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC与E、F两点,则阴影部分的面积是( )
A.1 B.2 C.3 D.4
8.已知坐标平面上的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对方向沿直线行走a,若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1,-) B.(-1,) C.(,-1) D.(-,-1)
9.如图,△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△EDC,使点B的对应点D恰好落在AB边上,AC、ED交于点F.若∠BCD=α,则∠EFC的度数是(用含α的代数式表示) ( )
A.90°+1/2α B.90°-1/2α
C.180°-3/2α D.3/2α
10.等边△ABC如图放置,A(1,1),B(3,1),等边三角形的中心是点D,若将点D绕点A旋转90°后得到点D′,则D′的坐标( )
A.(1+,0) B.(1﹣,0)或(1+,2)
C.(1+,0)或(1﹣,2) D.(2+,0)或(2﹣,0)
二、填空题
1. 如图所示的图案由三个叶片组成,绕点 O 旋转 120° 后可以和自身重合,若每个叶片的面积为 4cm ,∠AOB 为 120°,则图中阴影部分的面积之和为 cm .
2. 如图,在等边中,,是上一点,且,绕点旋转后得到,则的长度为 .
3. 如图,将绕点顺时针旋转得到,若,,则的度数为 .
4 如图,在中,,将绕点顺时针旋转得,与交于,则 .
5. 如图,在中,,将绕点顺时针旋转,得到,延长交的延长线于点,则的长为 .
三.解答题
1.如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为 ;
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为 .(用含m,n的式子表示)
2.如图,已知在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
3.如图,在△ABC中,BA=BC,∠ABC=40°,将△ABC绕点B按逆时针方向旋转110°,得到△DBE,连接AD,CE.
(1)求证:△ABD≌△CBE;
(2)求∠ACE的度数.
4.如图,在Rt△ABC中,∠ACB=90°,AC=1,将△ABC绕点C按逆时针方向旋转得到△A'B'C,连结BB'.
(1)说明△CAA′为等边三角形;
(2)求△A'BB'的周长.
5.如图,在△ABC中,点D在边AB上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE,交AC于点F,且∠B=70°,∠A=10°.
(1)求证:AB=ED.
(2)求∠AFE的度数.
一.选择题
1.如图,已知△ABC中,∠C=90°
置,连接C'C,则∠C'CB的度数为( )
A.15° B.20° C.30° D.45°
2. 下列图形中,既是轴对称图形又是旋转对称图形的是
A. B.
C. D.
3.如图,在△ABC中,AC=18,得到△A′B′C,则下列说法错误的是( )
A.的长为5π B.A′C=18
C.∠BCA′=50° D.∠ACB=∠A′CB′
4.已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,∠ACD=∠BCE=α,直线AE与BD交于点F(交点F至少在BD、AE中的一条线段上),如图2,则∠AFB与α的数量关系为( )
A.∠AFB+α=180° B.∠AFB﹣α=90°
C.∠AFB=3α D.∠AFB=4α
5.如图,在等边三角形ABC中,D是边AC上一点,将△BCD绕点B逆时针旋转60°,得到△BAE,若BC=5,BD=4( )
A.AE∥BC B.△BDE是等边三角形
C.∠EAB=∠CDB D.△ADE的周长是9
6.如图,△ABC的顶点坐标分别为A(3,6),B(1,3).若将△ABC绕点C顺时针旋转90°,得到△A′B′C′,则点A的对应点A′的坐标为( )
A.(8,2) B.(9,2) C.(8,3) D.(9,3)
7.如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交边AD、BC与E、F两点,则阴影部分的面积是( )
A.1 B.2 C.3 D.4
8.已知坐标平面上的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对方向沿直线行走a,若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1,-) B.(-1,) C.(,-1) D.(-,-1)
9.如图,△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△EDC,使点B的对应点D恰好落在AB边上,AC、ED交于点F.若∠BCD=α,则∠EFC的度数是(用含α的代数式表示) ( )
A.90°+1/2α B.90°-1/2α
C.180°-3/2α D.3/2α
10.等边△ABC如图放置,A(1,1),B(3,1),等边三角形的中心是点D,若将点D绕点A旋转90°后得到点D′,则D′的坐标( )
A.(1+,0) B.(1﹣,0)或(1+,2)
C.(1+,0)或(1﹣,2) D.(2+,0)或(2﹣,0)
二、填空题
1. 如图所示的图案由三个叶片组成,绕点 O 旋转 120° 后可以和自身重合,若每个叶片的面积为 4cm ,∠AOB 为 120°,则图中阴影部分的面积之和为 cm .
2. 如图,在等边中,,是上一点,且,绕点旋转后得到,则的长度为 .
3. 如图,将绕点顺时针旋转得到,若,,则的度数为 .
4 如图,在中,,将绕点顺时针旋转得,与交于,则 .
5. 如图,在中,,将绕点顺时针旋转,得到,延长交的延长线于点,则的长为 .
三.解答题
1.如图,△ABC的顶点坐标分别为A(0,1),B(3,3),C(1,3).
(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为 ;
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为 .(用含m,n的式子表示)
2.如图,已知在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
3.如图,在△ABC中,BA=BC,∠ABC=40°,将△ABC绕点B按逆时针方向旋转110°,得到△DBE,连接AD,CE.
(1)求证:△ABD≌△CBE;
(2)求∠ACE的度数.
4.如图,在Rt△ABC中,∠ACB=90°,AC=1,将△ABC绕点C按逆时针方向旋转得到△A'B'C,连结BB'.
(1)说明△CAA′为等边三角形;
(2)求△A'BB'的周长.
5.如图,在△ABC中,点D在边AB上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE,交AC于点F,且∠B=70°,∠A=10°.
(1)求证:AB=ED.
(2)求∠AFE的度数.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
